ルンゲクッタにしても線形多段階法を使うにしても、実際に問題を解こうとい
う上ではいろいろ考えないといけないことがある。もっとも重要なことは、刻
み幅 ![]() をどうやって決めるかということである。
をどうやって決めるかということである。
実際問題としては、解いていくにつれて導関数の値が大きく変わるといったこ とは普通に起きる。このために、刻み幅が一定のままで計算していくというの は非常に無駄なことが多い。
無駄を減らすためには、局所誤差が小さい(解が滑らかな)ところは刻みを大 きく、逆に解が急にかわるところでは刻みを小さくしてやればよい。このよう な方法を可変刻み (variable step) 、あるいは適応刻み (adaptive step) と いう。
これにはいろいろな考え方があるが、通常使われるのは、局所離散化誤差を推 定して、それがある値以下になるようにするという方法である。
このための一つの考え方は、以下のようなものである。
誤差の推定値が求まったら、普通は次のステップを調節する。局所離散化誤差 の次数がわかっているから、それに応じてステップサイズを調整すればよい。 次数プログラムによっては、現在のステップでの誤差が予定した値よりも大き ければステップを小さくして計算し直すようになっているものもある。
実装(プログラムを作ること)が容易であることもあって、この方法はわり と広く使われている。が、かなり無駄が多い方法であるというのも確かである。 というのは、単に誤差の推定のためだけに、 50% の無駄な計算をしているか らである。まあ、 50% はたいしたことないという考え方もあるが、計算に何 日も掛かるというような状況なら 50% は無視できないので、まあ、なんとか したくなるのが人情というものである。
というわけで、もうちょっとうまい方法はないかということで、以下のような ことを考えた人がいる。
一般に、 RK型の公式では、最終的な値は
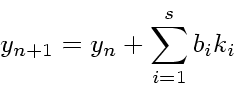 |
(1) |
 |
(2) |
この形の公式のことを埋め込み型 embedded 公式という。最初に提案した人の 名前をとって Runge-Kutta-Fehlberg 公式ということも多い。これもいろいろ 提案されているが、前回にも紹介した Dormand-Prince 公式はすべて埋め込み型であり、こ れが最近はもっとも広く使われている。精度が高いものが必要な時は、 8次の公式が使われる。これらは
http://www.unige.ch/math/folks/hairer/software.htmlから入手できる (Fotran と C がある)。
線形多段階法の場合、 RK と違って誤差の推定は容易である。例えば、アダム ス法で予測子・修正子ペアで使うなら、予測子と修正子の差は誤差の(オーダー としては)よい推定値になっている。したがって、この部分については面倒な ことは特にない。
問題は、実際に刻みを変えるほうである。もっとも一般的な方法は、「その場 で公式を導出する」というものである。これについて以下簡単に説明する。
アダムス法を使うには、要するに多項式補間の系数が出せればよい。以下、ニュー トン補間を使う方法を説明する。
補間したい関数 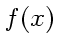 が、標本点
が、標本点
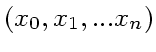 で、関数値
で、関数値
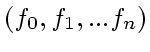 をとるとする。これを、以下のような形の多項式
をとるとする。これを、以下のような形の多項式
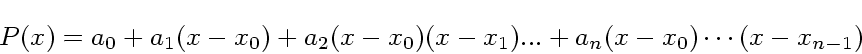 |
(3) |
まず、![]() については、
については、 ![]() とすればいいのは明らかであろう。
次に
とすればいいのは明らかであろう。
次に![]() であるが、
であるが、
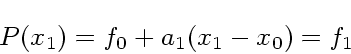 |
(4) |
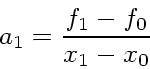 |
(5) |
![\begin{displaymath}
a_2 = \frac{f[0,2]-f[0,1]}{x_2-x_1}
\end{displaymath}](img24.png) |
(6) |
![\begin{displaymath}
f[i,j] = \frac{f_i - f_j}{x_i - x_j}
\end{displaymath}](img25.png) |
(7) |
さて、段々式が繁雑になるが、もうちょっとの辛抱である。上の形は、
![\begin{displaymath}
a_2 = \frac{f[2,1]-f[1,0]}{x_2-x_0}
\end{displaymath}](img26.png) |
(8) |
 を通る補間式
の一次の係数と、
を通る補間式
の一次の係数と、 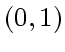 を通る補間式の係数の差みたいなものになっている。
を通る補間式の係数の差みたいなものになっている。
ここで、天下りに、 ![]() 階差商 (divided difference)
階差商 (divided difference)
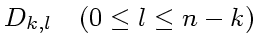 というものを導入する。これは以下のように定義される。
というものを導入する。これは以下のように定義される。
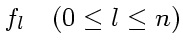 |
(9) | ||
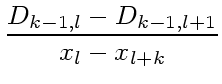 |
(10) |
 |
(11) |
証明には、![]() が、
が、 ![]() から始まる
から始まる ![]() 点を通る補間多項式の係数
であるということを用いる。定義により
点を通る補間多項式の係数
であるということを用いる。定義により
 |
(12) |
 |
(13) |
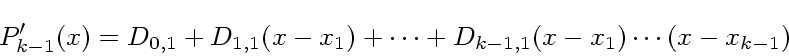 |
(14) |
 |
(15) |
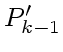 の最高次の係数であることに注意すると、
の最高次の係数であることに注意すると、
さて、
 |
(16) |
 が求める補間多項式であり、
が求める補間多項式であり、
と、こんな風に差商を作っておくと、これから多項式の係数を機械的に計算し
て積分して、、、、ということができる。さらに、差商の形でデー
タをとっておくと、上の漸化式を使って![]() を順番に更新することができる。
これは Krogh 型の公式と呼ばれ、かなり広い範囲の問題について、もっ
とも効率が良い公式であることがわかっている。
を順番に更新することができる。
これは Krogh 型の公式と呼ばれ、かなり広い範囲の問題について、もっ
とも効率が良い公式であることがわかっている。
なお、上の方法で時間刻みを変えられるなら、出発公式は不必要になることに 注意しておく。つまり、最初は1次の予測子、2次の修正子から出発して、ステッ プ毎に次数をあげていけばいい。ステップサイズは次数を考慮して決めておく。