数値計算をした時には、必ず答が合っているかどうかチェックしなければなら ない。
解析解があるような問題であれば、解析解と比べればいいわけだが、実際に数 値計算するのは解析解が求められないからするわけであって普通は解析解と比 べることはできない。
微分方程式の初期値問題の場合、チェックは例えば以下のようなことをするこ とになる。
最初の、計算精度を変えた時の解の振舞いを調べるというのは、例えば今やっ
ている重力多体問題の例なら計算機終了時の全粒子の位置、速度をとっておい
て、時間刻み
や見込み角 
を変えた時にどう動くかを見るというもの
である。原理的には、誤差は や見込み角 の何乗かに比
例するわけなので、それぞれ3種類くらいやってみてその差をとって、それが
理屈にあっているかどうか確認する。
ただし、この方法はいつでも使えるというわけではないことに注意する必要が ある。あまりうまく使えないのは、元の方程式の解がカオス的なものを長時 間数値計算するような場合である。
カオスの定義にはいろいろあるが、基本的な性質の一つは、「非常に近い初期 条件から出発した2つの系が、時間の指数関数で離れていく」というものであ る。ところが、大抵のハミルトン力学系で数値計算したいようなものはこの性 質をもつ。
特にいま考えているような自己重力多体系の場合、軌道が指数関数的に広がる 時間スケールは割合短く、典型的な粒子(星)の軌道周期の数分の1程度である ことがわかっている。つまり、例えば 10 周期とか計算すると、最初は非常に 近くにあった粒子の位置や速度が、無限に正確に数値積分しても大きくずれて くるということになる。
そんなふうにずれてしまうのであれば数値計算しても意味がある答は得られな いのではないかという気がするかもしれない。これはなかなか難しい問題で、 現在のところ完全に理解されているとはいいがたい。この話を始めるといくら やっても終わらないのでちょっとこれは棚上げ。
保存量は、ハミルトン系ならエネルギーがあるし、また系の重心の速度、系の 全角運動量といったものは保存するはずである。従って、こういったものがあ まりに大きく変わっていてはよろしくない。問題は「あまりに大きい」という のがどれくらいかだが、これは時と場合による。つまり、数値計算から引き出 したい答にエネルギー等の誤差がどれくらい影響しているかによる。これは実 際にチェックしなければいけない。「これくらいの誤差ならいいだろう」と思っ てなんとなく計算し、論文まで出してしまってから実は計算誤差のせいで結果 が間違っていたと判明した例はいろいろある。
というわけでエネルギー等をチェックする関数は以下の通り。といってもここ では誤差等をプリントアウトするだけである。
pt minus 1 pt
double kinetic_energy(particle * pp,
int n)
{
double ke = 0;
for(int i = 0;i<n;i++) {
ke += (pp[i].vel*pp[i].vel)*pp[i].mass*0.5;
}
return ke;
}
double potential_energy(particle * pp,
int n)
{
double pe = 0;
for(int i = 0;i<n;i++) {
pe += pp[i].phi*pp[i].mass;
}
return pe*0.5;
}
void print_energies(particle * pp,
int n,
int check)
{
static double etot0;
double pe = potential_energy(pp,n);
double ke = kinetic_energy(pp,n);
double etot = pe+ke;
if (check==0 ) etot0 = etot;
cerr << "etot = " << pe+ke << " PE=" << pe << " KE="<<ke << " V.R.= " << -ke/pe;
if(check)cerr << " de=" << (etot-etot0)/etot0;
cerr <<endl;
}
細かく関数が分かれているが、ここまで分けなくてもいいかもしれない。運動
エネルギー、ポテンシャルエネルギーはそれぞれ定義式
 |
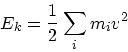(3) |
 |
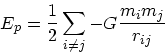(4) |
 |
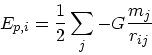(5) |
もちろん、近似的に計算機した結果、エネルギーが保存しない理由に2種類で てきてしまうことに注意する必要がある。つまり、一つは加速度の誤差がつもっ て粒子の位置が変わるせいだが、それとは別にポテンシャルエネルギー自体の 計算誤差もあるわけである。
関数 print_energies の中では、最初に呼ばれた時にはエネルギーを とって置き、その後呼ばれた時にはそのとって置いたエネルギーと比べること で誤差を計算する。
とっておくための変数が
static double etot0;
と宣言された変数 etot0 である。ここで static というのは、
この講義の1回目で説明したことに資料ではなっているが記憶にないのでもう
一度説明しておく。
Cは再帰呼びだしが可能な言語であり、関数のローカル変数は普通は呼ばれた 時に生成される（自動変数）。
static をつけておくと、どこか固定されたアドレスにとられる。このた めに、呼ばれた後も値が残っていて、関数が次に呼ばれた時もその値をおぼえ ている。従って、それと新しい値を比べることができる。 static がないと関数が呼ばれた時点でメモリ上に場所がとられるので、 前に呼ばれた時の値はどっかに消えてしまう。
直感的になにかおかしいことがないかどうかを見るには、数値解を視覚化して みるのが有効なことが多い。目でみてそれらしいものだったからといって合っ ているとは限らないが、ひと目みておかしいとわかるということは多いからで ある。
というわけで、全粒子の投影図をステップ毎に書いて見ることにしよう。例に よってPGPLOTを使う。
pt minus 1 pt
void initgraph()
{
if(cpgopen("") !=1 ) exit(-1);
cpgask(0);
}
void plot_particles(particle * p,
int n,
double xmax,
int first)
{
static float * xp;
static float * yp;
static int nbuf = -1;
cpgbbuf();
if (first == 1){
cpgpage();
cpgenv(-xmax, xmax, -xmax, xmax,1,-2);
}
if ( nbuf < n){
if (nbuf > 0){
delete [] xp;
delete [] yp;
}
xp = new float[n];
yp = new float[n];
nbuf = n;
}
for(int i = 0;i<n;i++){
xp[i] = p[i].pos[0];
yp[i] = p[i].pos[1];
}
cpgeras();
cpgbox("bcnst", 0.0, 0, "bcnst", 0.0, 0);
cpglab("X", "Y", " ");
cpgpt(n,xp,yp,-1);
cpgebuf();
}
最初の関数initgraph はこれも第一回の講義ででてきたものと同じで、 出力先を選んでことがPGPLOT自体の初期化をする関数を呼ぶだけである。
次の関数plot_particlesが実際に点々を打つ。といっても本当に点を 打っているのは関数 cpgpt で、それ以外は全部そのための準備と後始 末である。まず、 cpgpt は点列の座標を 2 つの1次元配列で受け取る ので、粒子データからそこにコピーする必要がある。さらにその前にそもそも 配列のデータ領域を確保する必要があるので、最初に呼ばれた時か、 または n の値が大きくなった時にはメモリを取る。
最初に呼ばれたかどうかの判断は、この配列に関しては static 変数 nbuf の値を見て行う。static 変数の宣言のところで値を設定しておくと、 これはプログラムの開始の時に一度だけ値が入る。従って、その値になってい れば最初に呼ばれた時であるということになる。
なお、最初に呼ばれた時に画面サイズの設定もするが、これは別に変数を使う ことにしておく。これは、実行中にプロット範囲を変えたいとかいうことに対 応できるようにしておくためである。(まあ、このへんはどうでもいいような 話ではある)
PGPLOTの実数型の引数は double ではなく float である。引数が配列でない 場合にはこれらは区別する必要はないが、配列の場合にはちゃんと float で 渡して置く必要がある。配列でない場合には、 C/C++ 言語には float と書いておいても実際には double に勝手に変換されるというよく理由 が分からない規定があるので区別しなくていい、というか区別しようがないこ とになる。
このあたりを付け加えたので、もう一度 main関数を書いておこう。
pt minus 1 pt
int main()
{
particle * pp;
int n;
cerr << "Enter n:";
cin >> n ;
pp = new particle[n];
double rsize = 1.0;
cerr << "Enter power index:";
double power_index;
cin >> power_index ;
cerr << "power index = " << power_index <<endl;
create_uniform_sphere(pp, n, power_index , rsize);
bhnode * bn = NULL;
int nnodes = n*2+100;
bn = new bhnode[nnodes];
double eps2;
double theta;
double dt;
double tend;
int iout;
cerr << "Enter eps2, theta, dt, tend, iout:";
cin >> eps2 >>theta >>dt >>tend >> iout;
cerr << "eps2=" << eps2 << " theta=" <<theta <<" dt=" << dt
<< " tend=" << tend << " iout=" << iout <<endl;
double xmax_plot;
cerr << "Enter xmax for plot:";
cin >> xmax_plot;
cerr << "xmax for plot = " << xmax_plot <<endl;
initgraph();
plot_particles(pp,n,xmax_plot,1);
calculate_gravity(bn,nnodes,pp,n,eps2, theta);
cerr << "Initial data"<<endl;
print_energies(pp,n,0);
int istep = 0;
for(double t=0;t<tend; t+=dt){
integrate(bn, nnodes, pp, n, eps2, theta, dt);
istep++;
plot_particles(pp,n,xmax_plot,0);
if (istep % iout == 0){
cerr << "Time=" << t+dt <<endl;
print_cm(pp, n);
print_energies(pp,n,1);
}
}
return 0;
}
段々入力するものが増えて来たので、例えば以下の ようなものをファイルで準備しておいて、
4000 -0.5 0.001 0.8 0.01 10 25 2リダイレクトを使って実行するほうが間違って変な値を入れることが少ないし 手間も減るだろう。ファイル名が samplein なら以下のようにすればいい。
# treecode < samplein
というわけで今日はこれくらい。