ここで述べる手法は、とりえあえず定義域があまり変な形をしていなくて(と いうのをちゃんと定義することはできるが、やると話が長くなるので省略)、 関数はその定義域のなかで連続で極小値を1つだけ持つという場合のためのも のである。
この場合、目的関数![]() が2階微分を持てば、原理的には話は極めて簡単になっ
て、
が2階微分を持てば、原理的には話は極めて簡単になっ
て、![]() という方程式をニュートン法で解けばいい。が、多くの場
合にこれはあんまりうまくいかない。というのは、変数の数
という方程式をニュートン法で解けばいい。が、多くの場
合にこれはあんまりうまくいかない。というのは、変数の数 ![]() が多くなる
と計算しないといけない2階微分の数は
が多くなる
と計算しないといけない2階微分の数は ![]() に比例して増えるわけで、計算
量が増えるだけでなく書かないといけないプログラムの量が増えるという問題
があるからである。
に比例して増えるわけで、計算
量が増えるだけでなく書かないといけないプログラムの量が増えるという問題
があるからである。
微分を数値的にやればいいのではとも考えられるが、これも丸め誤差等の影響 があって難しい場合が多い。
もっとも、微分を数値的にやるのではなく、数式的にやる、つまり、もとの関 数の数式から数式処理プログラムに生成させたり、あるいはプログラム自体を 「微分」する、つまり、目的関数を計算するプログラムから微分を計算するプ ログラムを自動生成するといった研究もかなり進んではいる。実際に問題を解 こうという時には、こういった手法が使えないかどうかも考えてはみるべきで あろう。
というわけで、以下はニュートン法とかではない方法。まず1変数、それから 多変数にいく。
まあ、1変数ならニュートン法でいいのではないかとも思うわけだが、多変数 の場合のための準備ということで一応説明しておく。実際には、多変数の問題 を解く時に形式的には1変数の問題の繰り返しになって、そこでは簡単には2階 微分が計算できなくてニュートン法というわけにはいかないので、それ以外の 方法がいるわけである。
良く本に載っているのは、黄金分割法というものである。これは、以下のよう
な方法である。区間![]() のなかに関数
のなかに関数 ![]() の最小値があることはわかっ
ているとする。
の最小値があることはわかっ
ているとする。
なお、一般には別に黄金分割でなくても、区間内に適当に2点とってその大き い方を新しい区間の端にするというので構わない。黄金分割のミソは上の説明 の「細かいこと」、つまり、分割点の一方を使い回せるので反復一度について 関数計算が1度ですむということである。
一度ですむのはいいが、収束は遅い。一度反復した時に区間の幅が ![]() にしかならないからである。これはつまり一次収束で、反復毎に定数分の1に
なるものである。
にしかならないからである。これはつまり一次収束で、反復毎に定数分の1に
なるものである。
もうちょっと賢い方法としては、疑似ニュートン法的なものがある。要するに 3点あれば2次関数で近似できるので、その極値を求めようというものである。 最適化問題ではない非線形方程式では Secant 法と呼ばれているものの拡張で ある。 Secant 法程速くはないが、 一次よりも速い収束をすることが知られ ている。
多変数の場合にも、黄金分割にあたるような直接探索法というのはあることは
あるが、あんまり使えないので省く。大抵の本で最初に出ているのは最急降下
法というものである。とりあえず、関数![]() が
が![]() 次元ユークリッド空間全体で定
義されているとする。この方法の原理は、「ちょっと動いた時にもっとも関数
値が減る方向に動く」というのを繰り返すことである。もっとも減る方向は、
次元ユークリッド空間全体で定
義されているとする。この方法の原理は、「ちょっと動いた時にもっとも関数
値が減る方向に動く」というのを繰り返すことである。もっとも減る方向は、
| (1) |
最急降下法のよいところは、いつかは収束することであり、よくないところは 収束が必ずしも速くないことである。これは、2変数で目的関数が2次形式の場 合についていろいろ実験したり考えてみたりすればわかるが、結局直交する2 方向の繰り返しに陥ってしまうからである。この事情は多変数の場合でも同じ で、結局2方向になっていくということが証明されている。
というわけで、速く答を出そうとするなら、やはり疑似ニュートン法的なもの を考えたくなる。1変数の時のように簡単に2次形式の近似式が構成できるわけ ではないが、その辺をなんとかうまくやろうというわけでいろんな方法が提案 されている。
多分良くつかわれているのは DFP(Davidon-Fletcher-Powell)法や BFGS(Broyden-Fletcher-Goldfarb-Shanno)法で、どちらも考案者の名前である。 時々 Variable Metric method(可変計量法) と呼ばれることもある。
以下、基本的な考え方を説明する。
目的関数が、以下の2次形式
| (2) |
ニュートン法では、![]() を2次形式で近似してそれの極値を求める。形式的に
は、近似値
を2次形式で近似してそれの極値を求める。形式的に
は、近似値 ![]() の回りでのテイラー展開
の回りでのテイラー展開
| (3) |
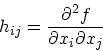 |
(4) |
| (5) |
目的関数が上の2次形式なら、これはもちろん
![]() で、正しい答が求まる。
で、正しい答が求まる。
そういうわけで、考え方としては、ヘッシアンなり ![]() の近似値を作ってい
こうというのが基本になる。
の近似値を作ってい
こうというのが基本になる。
ここで、ちょっと定義を続ける。まず、共役という概念を定義する。2つのベ
クトル ![]() が
が ![]() について共役であるとは
について共役であるとは
| (6) |
さらに、互いに共役な![]() 個のベクトル
個のベクトル
![]() を考え
を考え![]() 、これら
に対して、
、これら
に対して、
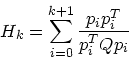 |
(7) |
| (8) |
これは、 ![]() が
が
![]() が張る部分空間では
が張る部分空間では ![]() みた
いなものであるということを意味している。したがって、
みた
いなものであるということを意味している。したがって、![]() を順番に発生
させる方法がなにかあれば、それを使って、
を順番に発生
させる方法がなにかあれば、それを使って、
ここでの実際的な問題は、互いに共役な ![]() を作るよい方法があるかどうかよく
わからないことである。一つの考え方は、反復による修正量
を作るよい方法があるかどうかよく
わからないことである。一つの考え方は、反復による修正量
![]() を使うことである。
を使うことである。 ![]() は共役ではないが、それでもなんと
か
は共役ではないが、それでもなんと
か
| (10) |
| (11) |
| (12) |
このように ![]() をとる一つの方法(DFP法)は、
をとる一つの方法(DFP法)は、
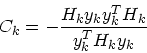 |
(13) |
まあ、自分でプログラムを書くならこれをつかうので OK であろう。ライブラ リとかだと BFGS のほうが少しよいようである。
さて、さっき共役な ![]() を作る方法はよくわからないと書いたが、これは
実はこれらの公式が作られた時に、作った人が知らなかったというだけの話で
実は別のところでは既に知られていた。それの応用が共役勾配法、すなわち
CG(Conjugate gradient)法である。これは形式的には簡単である。いま、
を作る方法はよくわからないと書いたが、これは
実はこれらの公式が作られた時に、作った人が知らなかったというだけの話で
実は別のところでは既に知られていた。それの応用が共役勾配法、すなわち
CG(Conjugate gradient)法である。これは形式的には簡単である。いま、
![]() と書くことにして、
と書くことにして、
| (14) | |||
| (15) |
![]() が2次関数の時には、これで求まる
が2次関数の時には、これで求まる ![]() は互いに共役であることを証明
できる。さらに、ちょっと変形すると、
は互いに共役であることを証明
できる。さらに、ちょっと変形すると、
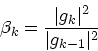 |
(17) |
なお、疑似ニュートン法、CG法のどちらの場合でも、方向は決まるが1次元問
題を繰り返し毎に解く必要はある。これは黄金分割なり疑似ニュートン法なり
を使うことになる。多次元の反復では勾配を求めないといけないので少なくと
も![]() 個の関数を計算することになるが、1次元問題では反復毎に1度
個の関数を計算することになるが、1次元問題では反復毎に1度 ![]() を計
算するだけなのでここではそれほど効率に気を使う必要はないことに注意。
を計
算するだけなのでここではそれほど効率に気を使う必要はないことに注意。
CG 法は現在最適化よりも大規模な線型方程式を解くのに広く使われている。
今、
| (18) |
| (19) |
何故こんなややこしいことをするのかと思うかもしれない。理由はちゃんとあっ て、一つはこの方法は反復法であるにもかかわらず原理的には有限回で収束す ること、もう一つはいろいろ工夫することで収束を非常に速くできることが多 いということである。
収束を速くするための工夫は色々な「前処理」と言われるもので、それだけを扱った本 がいっぱいあるのでここではこれ以上は扱わない。