3 ハミルトン系向けの方法

古典力学系のもっとも簡単な例といえば、一次元調和振動子、つまり、運動方程式では

$\begin{displaymath} \frac{d^2x}{dt^2} = -kx \end{displaymath}$

(17)

さて、このような、固有値が純虚数である、いいかえれば中立安定な場合、安定性解析はちょっと厄介になる。というのは、通常の意味で安定というのは、数値解がいつかは原点にいってしまうということ、いいかえればエネルギーが保存しないということを意味するからである。

つまり、安定領域のある公式では、ほとんどのもので虚軸上の一定範囲では数値解が「安定」になってしまう。つまり、本当の解はいつまでも振動を続けるのに、数値解は減衰してしまうのである。もちろん、タイムステップを大きくとれば、安定領域から外れるのが普通であり、振動しながら広がっていくような解になる。安定領域に虚軸を含まないような公式（例えば前進オイラー公式）の場合では、かならず軌道が広がっていくことになる。つまり、虚数軸が安定性限界になっていない限り、必ず軌道から一方的に外れていってしまうのである。

安定領域の話は先週ちょっとしたけど、もう一度まとめておく。つまり、線形常微分方程式

$\begin{displaymath} \frac{dy}{dx} = kx \end{displaymath}$

(18)

が複素数の場合も考えるのは、元の微分方程式が連立方程式なら固有値が実数でない場合もありえるからである。でもって、A安定とは、安定領域が左半平面全体を含むことである。これは、もとの方程式が安定なら数値解もかならず安定であるということ。もとの方程式が不安定でも数値解は安定になっちゃってるかもしれないが、これは気にしないというのがA安定の定義である。

つまるところ、線形系では安定性限界が虚数軸である（数値解に純虚数の固有値がある）というのが、数値解が厳密に振動的であるための必要十分条件ということになる。この時、数値解はもとの系の性質をある意味で良く表しているといえるであろう。

実は多変数の場合や非線形の場合でも本質的な事情は変わらない。ただし、こちらはまだいろいろ理論的にはっきりわかっていないことがいろいろある。が、大雑把にいうと同じような事情が成り立っている。つまり、もとが周期解であるときに、大抵の積分法では周期解から一方的にずれていく、つまり、保存量であるはずのエネルギー等が保存しなくなる。

もちろん、エネルギーが厳密には保存しないということが問題であるかどうかというのも実は難しい問題である。というのは、保存しないといってももちろん数値解の精度では保存しているわけだから、それでかまわないのではないかとも考えられるからである。

3.2 リープフロッグ公式

ハミルトン系のシミュレーションの例には例えば以下のようなものがある

これらはいずれも、古典的な多体問題として定式化される。プラズマの場合は磁場も入るのでちょっと面倒だが、それを無視すれば運動方程式が

$\begin{displaymath} m_i\frac{d^2\mbox{\boldmath$x$}_i}{dt^2} = \sum_{j\ne i} \mbox{\boldmath$f$}_{ij} \end{displaymath}$

(19)

このような問題に対して、もっとも普通に使われる公式は以下の leapfrog といわれるものである。

$\displaystyle v_{i+1/2}$	$\textstyle =$	$\displaystyle v_{i-1/2} + \Delta t a(x_i)$	(20)
$\displaystyle x_{i+1}$	$\textstyle =$	$\displaystyle x_{i} + \Delta t v_{i+1/2}$	(21)

$\begin{displaymath} v_{1/2} = v + \Delta t a(x_0)/2 \end{displaymath}$

(22)

$\begin{displaymath} v_{i} = v_{i-1/2} + \Delta t a(x_i)/2 \end{displaymath}$

(23)

$\displaystyle x_{i+1}$	$\textstyle =$	$\displaystyle x_{i} + \Delta t v_{i} + \Delta t^2 a(x_i)/2$	(24)
$\displaystyle v_{i+1}$	$\textstyle =$	$\displaystyle v_{i} + \Delta t [a(x_i)+a(x_{i+1})]/2$	(25)

$\displaystyle v_{i+1/2}$	$\textstyle =$	$\displaystyle v_i + \Delta t a(x_i)/2$	(26)
$\displaystyle x_{i+1}$	$\textstyle =$	$\displaystyle x_{i} + \Delta t v_{i+1/2} + \Delta t^2 a(x_i)/2$	(27)
$\displaystyle v_{i+1}$	$\textstyle =$	$\displaystyle v_{i+1/2} + \Delta ta(x_{i+1})/2$	(28)

この公式は局所誤差が $O(\Delta t^3)$ 、大域誤差が $O(\Delta t^2)$ である。

さて、局所誤差という観点からはこれは決して良い公式というわけではないが、現実にはこの公式は非常に広く使われている。

これは、別にもっとよい方法を知らないからとかではなく、実はこの方法がいくつかの意味で非常に良い方法であるからである。いくつかの意味とは、例えばエネルギーや角運動量のような保存量が非常によく保存するということである。これらの保存量については多くの場合に誤差がある程度以上増えない。

この、ある程度以上誤差が増えないというのは目覚しい性質である。通常の方法では、エネルギーの誤差は時間に比例して増えていく。従って、長時間計算をしようとすればそれだけ正確な計算をする必要がある。ところが、エネルギーの誤差は溜っていかないのならば、かならずしも精度を上げる必要はないとも考えられる。

もちろん、エネルギーが保存していればそれだけで計算が正しいということにはならない。が、理論的には、いくつかの重要な結果が得られている。まず、

Symplectic method については、以下のようなことが知られている

以下、まず数値例でこれらの性質を確認し、それからなぜこのようなうまい性質を持つのかについて直観的な説明を与えよう（厳密な説明／証明には力学系の積分可能性に関するかなり深い知識が必要となる）。

3.3 数値例

3.3.1 調和振動子

能書きを聞いていても良くわからないので、実例を見てみよう。まず、簡単な例として調和振動子

$\begin{displaymath} \frac{d^2x}{dt^2} = -x \end{displaymath}$

(29)

軌道とエネルギーを図に示す。非常に特徴的なのは、 leap frog ではエネルギーが周期的にしか変化しないのに対し、ルンゲクッタでは単調に増えていることである。

**Figure 1:** 調和振動子の数値積分。左：軌道。右：エネルギー。破線は2次のルンゲクッタ、実線は leapfrog の結果
$\begin{figure}\begin{center} \leavevmode \epsfxsize 7.5 cm \epsffile{leap1.eps}\epsfxsize 7.5 cm \epsffile{leap1a.eps}\end{center}\end{figure}$

ルンゲクッタでは単調に変化するというのは前に説明した通り（2階のルンゲクッタでは虚軸を安定領域に含まないため）である。さて、これに対し、 leapfrog ではエネルギーが変化していないが、これはどういうことなのであろう？

$\begin{displaymath} H' = \frac{1}{2}(x^2 + v^2) - \frac{h^2}{4}x^2 \end{displaymath}$

(30)

3.4 非線形振動

$\begin{displaymath} \frac{d^2x}{dt^2} = -x^3 \end{displaymath}$

(31)

軌道とエネルギーを図に示す。調和振動の場合と同様に、 leap frog ではエネルギーが周期的にしか変化しないのに対し、ルンゲクッタでは単調に増えている。

**Figure 2:** 非線形振動の数値積分。左：軌道。右：エネルギー。破線は2次のルンゲクッタ、実線は leapfrog の結果
$\begin{figure}\begin{center} \leavevmode \epsfxsize 7.5 cm \epsffile{leap3.eps}\epsfxsize 7.5 cm \epsffile{leap3a.eps}\end{center}\end{figure}$

この場合も保存量があるので、頑張れば求まるかもしれない。

3.5 シンプレクティック公式

さて、 leapfrog 公式は、上で見たようにハミルトン系に対してエネルギー誤差が有界に留まるという大きな特長がある。が、2次精度でしかない。もっと高次の方法はないのだろうか、またあるとすればどういう原理で作れるのだろうか。

高次の方法を構成する一つのアプローチが、シンプレクティック公式といわれるものである。これはなにかというと、積分公式がシンプレクティック写像になるように作るということである。

と、これでは意味がわかりませんね。シンプレクティック写像とは、ようするに正準変換のことである。正準変換とはなにかというのは解析力学を思い出してみて欲しいが、直観的には、力学系を不変に保つ、つまり変換まえの座標系で求めた軌道を変換したものと、変換後の座標系での力学系の軌道が厳密に同じになるようなものである。

ハミルトン力学系の解そのもの（ある時刻

での座標から、

での座標に移す変換）もシンプレクティックである。まあ、だから、シンプレクティックになっているような積分公式は、そうでないものに比べてなんとなく力学系の性質にあっているような気はする。

で、いいたかったことは何かっていうと、上の leapfrog 公式はこのシンプレクティック性を満たしているということだった。詳しくは、「数理科学」 1995年6月号にのった吉田による解説記事でもみてもらうことにして、ここでは高次の公式にはどんなものがあるかという話をしておく。

3.6 陽解法

陽解法の組み立て方はいろいろある。一つは、 RKN 系の公式で、係数をシンプレクティック性を満たすように決めるということである。これはここ10年で無数に論文がでた。4次、あるいは6次の公式としては、吉田や鈴木による作用素分解に基づく公式が良く知られている。

これらの方法の原理は、要するに上の leap frog をタイムステップを変えていくつか組合わせるというものである。うまくタイムステップを組み合わせると誤差の高次の項を消すことができるわけである。3段4次の公式、7段6次の公式等が吉田によって導かれている。

なお、実は陽解法はハミルトニアンが

の形の場合にしか使えないが、大抵の問題はこう書けることはいうまでもないであろう。

また、 RKN 系の公式を力任せに構成する試みもあり、4次から8次までの公式が作られている。計算精度という観点からはこちらのほうが leapfrog を組合わせるものよりも圧倒的にいいということがわかっている。

3.7 シンプレクティック公式の意味

さて、シンプレクティックであるということと、「良い」ということの間にはちゃんとした理論的な関係があるのであろうか？一応あるということになっている。つまり、あるハミルトニアン

で表される系をシンプレクティックな

次の公式を使って積分した解は、別のハミルトニアン

で与えられるシステムの厳密解になっていて、

と

の間に

$\begin{displaymath} H = H' + h^{p+1}H_p + O(h^{p+2}) \end{displaymath}$

(32)

なお、例えば上の調和振動子の場合には実際に数列が収束し、

が求まっている。が、これは極めて例外的な場合で、一般の場合には収束するかどうかも明らかではないようである。

収束するかどうか明らかではないのでは、使っていいことがあるという保証はないではないかと思うかもしれない。理論的にはその通りなのであるが、実際にはいろいろな問題に適用されて、従来の方法よりも高い精度が得られるということが確認されている。

3.8 シンプレクティック公式の問題点と対応

さて、式(32) をみるとわかるように、シンプレクティック公式に付随するハミルトニアン

には時間刻み

が入っている。従って、

をふらふら変えると

も変わって、結果的に求まった数値解は一つの力学系の軌道ではないなんか変なものになってしまう。ということは、可変時間刻みにするとシンプレクティック公式はうまく働かないのではないかということが想像される。

じつはその通りで、例えばシンプレクティックで埋め込み型のルンゲクッタというものを作って、実際に時間刻みを変えてみた人がいる。その結果、普通のルンゲクッタよりも良くならないということが発見された (1992年頃)。問題によってはこれは致命的な欠陥となるので、さまざまな対応法が精力的に研究されているのが現状である。が、あまり一般的にうまくいく方法というのは見つかっていないようである。つまり、 stiff な問題の場合にあったような、万能な公式というのはシンプレクティック公式に関する限り知られていない。

なお、シンプレクティック公式において普通に時間刻みを変えると、それはシンプレクティックではなくなるということが Gear と Skeel により一般に証明されている。彼らの結果は、時間刻みも含めて考えると、写像が時間方向に歪んだもの（もとの位置によって時間刻みが変わるため）になり、そのために元の公式がシンプレクティックであれば時間刻みを変えると必ずシンプレクティックでなくなるというものである。

それでは、時間刻みを変えるのは絶対に不可能かというと、以下のような考えかたでの研究が進められている。ハミルトニアン

を

$\begin{displaymath} H = H_1 + H_2 + \cdots \end{displaymath}$

(33)

もう一つのシンプレクティック公式の問題点は、「写像」であるということから一段法、具体的にはルンゲクッタ型の公式であるので、局所誤差に対する計算量という観点からは線形多段階法に比べて必ず悪いということである。

3.9 対称型公式とは

さて、まず対称型公式とはなにかということだが、まず時間反転に対する対称性というものを定義しておこう。時間反転に対する対称性とは、常微分方程式

$\begin{displaymath} \frac{dy}{dx} = f(x,y) \end{displaymath}$

(34)

$\begin{displaymath} y_{i+1} = F(x_i,y_i,f, \Delta x) \end{displaymath}$

(35)

$\begin{displaymath} y_i = F(x_{i+1},y_{i+1},-f, \Delta x) \end{displaymath}$

(36)

で、一段法の場合には、この意味で対称なものを対称型公式ということにする。

具体例で考えてみよう。例えば前進オイラー法は対称型ではない。これは、いった先で導関数を計算すれば、一般にもとのところでの導関数とは違うから当然であろう。前進オイラー法が対称ではないのだから、その逆写像である後退オイラー法も対称型ではないことになる。

では、対称型にはどういうものがあるかということだが、明らかに対称型であるものとしては、台形公式

$\begin{displaymath} y_{i+1} = y_i + \frac{h}{2} (f_i + f_{i+1}) \end{displaymath}$

(37)

がある。これが上の対称性を満たしていることはいうまでもない。

さて、なぜこの型の公式を考えるかということであるが、これは実はそれほど簡単な話ではない。実験的には以下のようなことが知られている。

前のほうの性質はシンプレクティック公式と同じであるが、後の方の性質はシンプレクティック公式よりもある意味でよいものである。

ここではとりあえず対称型公式にはどんなものがあるかという話をしておこう。

さて、一階の方程式に対する一段法という制限をつけた場合、つまり、ルンゲクッタ法の場合、対称な公式はかならず陰的公式になる。逆に、陰的公式であれば対称型のものを作るのは容易である。つまり、ルンゲクッタ法を与える行列

とかベクトル

が対称になっていればいい。

何度もでてきたので予想されるかもしれないが、陰的ガウス法は対称型公式でもある。

一階の系に対する一段法では、そういうわけですでに紹介してきた陰的 RK のほかにうまい方法があるわけではない。それでは、

3.10 ハミルトン系用の陽的対称型RK公式

実は、すでに述べたように、 leapfrog 公式は対称型でありしかも陽公式である。で、 leapfrog の組合わせで作られる公式も、実はすべて対称型になっている。

3.11 対称型線形多段法

まず、線形多段階法に対する対称性の定義を与える必要がある。ここでは、以下のように定義しておこう。 2階の方程式用の線形多段階法は、一般に

$\begin{displaymath} \alpha_0 x_{i+p} + \cdots \alpha_p x_{i} = h^2 (\beta_0 f_{i+p} + \cdots \beta_p f_{i}) \end{displaymath}$

(38)

$\begin{displaymath} \alpha_i = \alpha_{p-i}, \quad \beta_i = \beta_{p-i} \end{displaymath}$

(39)

$\begin{displaymath} x_{i+1}-2x_i + x_{i-1} = h^2 f_{i} \end{displaymath}$

(40)

上の意味で対称な公式は、実際に時間反転に対して対称であるということに注意しておこう。つまり、 $(x_i, ... x_{i+p-1})$ から上の式で $x_{i+p}$ を求めたとする。時間を逆転させた解を考えて、 $(x_{i+p}, ... x_{i+1})$ から $x_{i}$ を求めるということを考えても、使う式が時間が逆転していないものと同じになっているのである。

このような公式は、 1970 年代から知られていたが、注目されるようになったのは 1990 年代に入ってからである。特にトロント大の Quinlan, Tremaine らが14次までの対称型公式を導いた。表1にその値を示しておく。

なお、非常に最近になって、国立天文台の福島によって、Quinlan & Tremaine によるものよりもはるかに良い性質を持つものが導かれている。

ただし、これらの公式に共通する欠陥として、線形解析では安定であっても、非線形問題（例えば、単純なケプラー問題）に適用すると不安定な振動を起こすことがあるという困難があり、これはまだ未解決の問題である。

**Table 1:** Quinlan & Tremaine 1990 による対称型公式の係数
$\begin{table}\begin{center} \leavevmode \epsfxsize\textwidth \epsffile{QuinlanTremain1990tab2.ps}\end{center}\end{table}$

3.12 エルミート型公式

一般に対称型というわけではないが、4次の対称型公式を導く特別な方法としてエルミート型（あるいはエルミート・オブレヒホフ型）と呼ばれる公式のクラスについてここで触れておこう。

エルミート型公式は、線形多段階法のアダムス型公式の一つの一般化である。どのような意味において一般化であるかというと、アダムス型と同じように補間多項式を積分することで新しい時刻での値を求めるところは同じである。違うところは、アダムス型公式では補間多項式を作るのに関数の値を使う（ラグランジュ・ニュートン補間）が、エルミート型公式では、関数の導関数の値も使うのである（エルミート補間）。

もっとも単純な発想としては、テイラー法というものがある。つまり、微分方程式

$\begin{displaymath} \frac{dy}{dx} = f(x,y) \end{displaymath}$

(41)

$\begin{displaymath} \frac{df}{dx} = \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} \frac{dy}{dx} \end{displaymath}$

(42)

高次の導関数が簡単に求められる場合（例えば線形な系とか）には、この方法はかなり強力である。線形多段階法やルンゲクッタに比べて誤差項の係数がずっと小さく、タイムステップが大きくとれるからである。

が、多くの問題において、高階導関数の直接計算は現実的ではない。これは、計算量が指数関数的に爆発するのが普通だからである。とはいえ、

の一階導関数や二階導関数くらいならば指数関数的といってもたかがしれている。しかしながら、これではテイラー法では2次や3次の公式しか作れない。実用的な公式としては、（leap frog のような特別に良い性質をもっているとかいうのでなければ）もうちょっと高次のものが必要である。

そこで考えられるのが、高階導関数を使ってさらにルンゲ・クッタ型とか線形多段階法のような公式を作ることである。例によってもっとも簡単な場合というのを考えると、それは

と $y_{i+1}$ のところで

の一階導関数の値を使うもの（高次導関数を使わないものであれば台形公式に相当）の一般化ということになろう。

台形公式は、2次の陰的アダムス型公式と考えることができる。つまり、

を線形補間してそれを積分しているわけである。これに対し、

と

を使う補間というのはどういうものかということを考えてみると、これは 3次多項式を構成できることがわかる。具体的には、導関数の近似多項式を

$\begin{displaymath} f(x_0 + h) = f_0 + a h + \frac{b}{2} h^2 + \frac{c}{3!} h^3 \end{displaymath}$

(43)

$\displaystyle a$	$\textstyle =$	$\displaystyle f_0'$
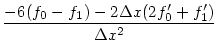$\displaystyle b$	$\textstyle =$	$\displaystyle { -6(f_0 - f_1) - 2\Delta x (2 f_0' + f_1') \over \Delta x^2}$
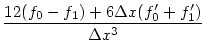$\displaystyle c$	$\textstyle =$	$\displaystyle { 12(f_0 - f_1) + 6\Delta x (f_0' + f_1') \over \Delta x^3}$	(44)