さて、硬い微分方程式とは何かということだが、例えば以下のような化学反応 系を考えてみる
各物質の濃度を 
と書くことにすれば、それぞれの従う方程式は、
例えば
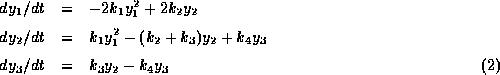
というようなものになる。
係数がたくさんあって面倒なので、以下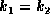 
, 
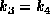とし、初
期条件として
という場合だけを考えることにする。
図1
に、 
として、前進オイラー法および後退オイラー法で
解いた場合の数値解の例を示す。この時の定常解は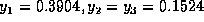 
というところになる。グラフに示しているのは 
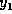と
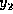である。
滑らかに収束しているのは、前進オイラー法で 
ととった
ものと後退オイラー法で
ととったものである。これに対し、振動的に発
散してしまっているのは前進で 
の場合である。非常に点
が荒く、途中での誤差が大きいが最終的には真の値にいっているのは、後退オ
イラー法で
と極端に刻みを大きくしたものである。
なお、この計算例では、保存則
を利用して、方程式から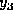 
を消している。
化学反応系のような非線形の方程式系では、上の例のように速度定数が大きく
違うということはそれほど珍しいことではない。上の例では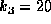 
であ
るが、これが何桁も大きい場合というのもある。例えば、化学反応といっても
天体物理で出てくるような核化学反応を考えると、速度定数が 10桁くらい違
うものが出てくることはそれほど珍しくない。
こういった場合にどういう方 法を使うべきかというのが今日考えていきたいことである。
最初に見たように、例えば化学反応系などでタイムスケールが非常に違うと具 合の悪いことが起きるわけであるが、この具合の悪さというのは具体的にはな にかというのが問題である。
例によって、方程式が線形の場合について考える。非線形の場合は、局所的に 線形化することで硬さを定義することになる。非斉次の線形常微分方程式
の一般解は
で与えられる。ここで、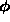
は方程式(5) を満たす特殊解
である。
さて、この方程式が安定であるとすれば、固有値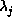 
はすべて実部
が負である。ところで、前回の安定性領域についての議論でちょっと話したよ
うに、大抵
の数値解法は絶対安定性領域が左側に有界である。これは、言い替えると、時
間刻み h を、適当な定数 M を使って
という制限を満たすようにとらないといけないということを意味する。 M は実際には安定性領域の左側の限界値ということになる。
さて、こういった問題で、どのあたりまで計算しないといけないかというのを 考えると、実部の絶対値が最小の固有値に対応する成分が十分小さくなるまで ということになる。従って、必要なステップ数は、
に比例する程度ということになる。つまり、この値が大きいと、計算が非常に 大変になるのである。この値のことを硬さ stiffness といい、これが「非常 に大きい」ときに方程式が硬いという。
どれくらい大きい時に硬いというかは曖昧であるが、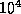 
を越えると硬い
といって間違いない。実用上は、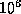 
を越えることも珍しくない。
なぜ「硬い」といわれるかという歴史的な事情を紹介しておくと、このような 問題は、もともとは機械制御系、つまり、モーターで棒かなにかを回してその先 の位置をセンサでフィードバックして制御するようなもので発見された。棒を 振り回すとこれは変形するが、棒が「硬い」ほどその変形の周期が短くなる、つま り固有値の絶対値が大きくなるわけである。
なお、この例からわかるように、本当は固有値の虚数部分も問題である。
非線形方程式
の場合には、そのヤコビアン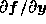
によって局所的
に線形化した方程式について硬さを定義する、つまりはヤコビアンの固有値か
ら決まるということになる。
さて、この硬さというのが問題かどうかということであるが、仮にある公式の
絶対安定領域が左半平面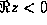 
全体を含んでいれば、硬かろうがなん
だろうが問題ではないということはすぐにわかるであろう。この、絶対安定領
域が左半平面を含むという性質を、ダールキストは A-安定性と名付けた。
A-安定性については、ダールキスト自身による次の否定的な結果がある
証明は面倒なので省略する。
これに対し、陰的ルンゲ・クッタ公式については以下の素晴らしい結果が知ら れている
陰的 RK 法はどんなものかという話をしてなかったですね。陰的 RK には陽的 RK 以上に無限にいろんなバリエーションがあり得るが、特に硬い方 程式に使われる方法はほとんど collocation method といわれるものになって いる。Collocation method の基本的な考え方は、「数値積分の公式をそのま まなんとか常微分方程式の解法に置き換えるために、数値積分を使って RK 法 の途中の点での解を求める」というものである。
といっても、これではなんだかわかりませんね。例によってまずもっとも簡単 な場合というのを考えてみる。
簡単な数値積分の公式といえば、中点公式か台形公式である。どちらも2次精 度である。以下、中点公式を考える。
中点公式は、
とするものである。微分方程式
に中点公式を使おうという時に困るのは、 y の値に何をいれればいいかわ からないということである。
この困難は、数値積分が近似多項式の積分として与えられたということを思い
出せば一応解決できる。中点公式の場合、数値積分ではこれはfを
で近似するということに相当した。同様なアイディアを微分
方程式に適用すれば、微分方程式の場合、 fを定数で近似し、解で
ある y を一次式で近似する、つまり
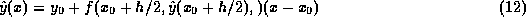
という近似をする。これから、問題の中点での値を 
と書くと
と書けるわけで、これは 
に対する代数方程式になっている。これを
解けば数値解も求まるわけである。これで求まった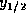 
を使って、次
の数値解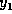 
は
と書ける。
数値積分と同じように、途中にとる点の数（RKでは段数に相当）をあげれば近
似の次数が上がって精度をあげられる。普通の考え方は、点がn個なら
n-1次多項式ができる。ここでは途中の点の x 座標を 
と
書き、構成されたn-1次多項式を 
と書くことにすると
での「解」 
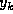について
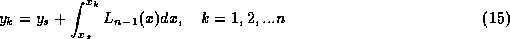
がなり立つ。ここで 添字 s がつくのはステップの最初の値である、さらに
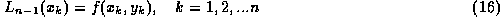
がなり立つように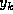 
と L を決め、それを積分して 
での解が求
まるということになる。
と書くと非常に大変そうだが、係数をあらかじめ計算しておけば上の手続きが 陰的ルンゲクッタ公式として表現できる。
途中の点のとりかたであるが、普通に考えつく方法は等間隔のラグランジュ補 間で、両端を含むようなものである。これは点の数 n に対して次数が n で、まあ悪くはない。また、両端の点を含むので、左端は計算しなくていいこ とになりちょっと嬉しい。
が、数値積分については、うまく点をとると n個で最大 2n 次を達成できると いう邪道な結果が知られている。もっとも高い次数を達成できるのは、n個 の点をn次ガウス・ルジャンドル多項式の零点にとるもので、これを普通陰 的ガウス公式という。これは2点で4次とか4点で8次の精度が達成できるなかな か結構な公式である。
さらに結構なことに、上に述べたA-安定になっているわけである。
さらに、ルジャンドル多項式の性質（対称性）から、陰的ガウス公式は時間反 転に対して対称であり、さらにあろうことかシンプレクティックでもあるとい うことがわかっている。なお、これらのことからわかるように、陰的ガウス公 式では安定領域がちょうど左半平面全体であり、虚軸が境界になっている。
この、虚軸が境界になっているというのはまあ結構な性質ではあるが、問題に よってはもっと強力に振動を押え込みたいということもある。このような場合 には、次数が1下がるが Radau 法のような、右端の点を含む公式を使うことが ある。このへんのコードも前に紹介した Web サイトにある。
前節で見たように陰的ガウス法は A-安定であり、基本的にはこれを使えば方 程式が硬いということによる問題は起きないといっていい。が、実用上は、こ の方法にはあまり嬉しくない特性、つまり、大規模な非線形代数方程式を解か なければいけないという特性がある。
もちろん、線形多段階法のところで考えたような逐次（直接）代入法で答が収束すれば、 これはたいした問題ではない。しかし、実はこれはうまくいかない。つまり、 陰的ルンゲ・クッタに対する逐次代入が収束する条件は リプシッツ連続条件
が成り立っている時に、
( C は公式によって決まる定数だが、1 に
近い)で与えられる。ところが、 L は定義から固有値の絶対値の最大値に等
しいので、結局陽的な公式と同じように最大固有値でタイムステップが決まっ
てしまい、逐次代入法ではA-安定性が失われてしまうのである。
それではいったいどうすればいいかということだが、要するに逐次代入なんて いう手抜きな方法を使わないで、もうちょっとまっとうな方法を使えばいいの である。通常使われるのはニュートン法による反復、つまり、方程式を局所的に線形化し、 その線形方程式の解を新しい近似解にする方法である。
原理を後退オイラー法の場合について説明しよう。もちろん、高次の陰的ルン ゲクッタやあとに述べる陰的線形多段階法でも理屈は同じである。後退オイラー 法の場合、解くべき方程式は
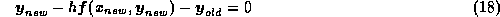
である。ニュートン法による i 回目の近似値を
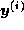と書くことにすると、
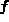が 
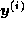の回りで
と線形化されるから、 
を求めるには以下の方程式
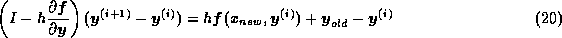
を解けばいいわけである。
すぐにわかるように、ニュートン法は方程式が線形であれば硬さに無関係に一 回で収束する。つまり、逐次代入法とは違ってA-安定性を保てる。
方程式が非線形の場合にうまくいくか、また、どれくらいの反復回 数でうまくいくかというのはなかなか難しい問題である。良く知られているよ うに、ニュートン法は二次収束する、つまり、初期推定が十分に良ければ誤差 が一回反復するとまえの誤差の2乗程度まで小さくなるという性質（これは、2 次の項の大きさからすぐに証明できる）があるので、うまい初期値が得られれ ば反復回数は少ない。
が、うまい初期値をとる一般的な方法はない。例えば陽的ルンゲクッタや陽的
な線形多段階法で初期値を作ることも考えられるが、これは系が硬い時には悪
い推定値を出す可能性もあるからである。比較的うまくいくのは、なにも考え
ないで
とする、また陰的ガウス公式であれば途中の
値についてもそうする方法である。
なお、もともとのニュートン法ではヤコビアンを反復毎に計算し直すが、これ らの方法を実装する時には、「収束しているうちはヤコビアンをそのまま使う」 という方法で計算量を減らすのが普通である。
ここまでで見たように、ガウス法などの陰的ルンゲクッタは硬い方程式にたい して非常によい性質をもつが、一つ大きな問題がある。それは、ニュートン法 で解く方程式の大きさが、元の方程式の本数 N と公式の段数 p の積 Np に比例するということである。
ニュートン法で方程式を解くときに、 LU分解（普通のガウスの消去法のこと と思っていい）を使うとすれば、計算量が行列の次元の3乗で増える。つまり、 公式の段数の3乗ということになる。これでは、せっかく高い次数の公式が作 れるといっても実用性は低い。
ニュートン法ででてくる線形化した方程式自体を、LU分解ではなく適当な反復 法、たとえば Gauss-Seidel 法、 SOR、共役勾配(CG)法といったもので解くこ とも考えられるが、これらを使うとまたA-安定性が失われたりすることになる。
これらの問題をあるていど回避するため、非常にさまざまな公式群が研究され ている。以下にその例をあげる
前に述べたように、計算量と精度の関係を見た時に線形多段階法はルンゲクッ タに比べてかなり良いのが普通である。従って、線形多段階法で比較的よい性 質をもつものはないかということを考える。
ダールキストの結果によって、A-安定では2次以上にならないということがわ かってしまっているので、A-安定の条件のほうをちょっと緩めてみる。緩め方 にはいろいろあるが、ギア (C. W. Gear) の提案は、図2の ように原点近くで虚部が大きいところでは不安定でもいいということにしよう というものである。
ギアはこのような領域で安定であることを硬安定ということにした。さらに、 以下の形の公式
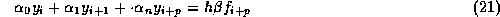
であれば、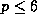 
の場合には硬安定な公式が存在することを示した。
係数の表は適当な参考書をみること。
実際のプログラムの例は例えば http://www.netlib.org/ode/cvode.tar.gz といったものを見てみること。
これは無数にある。名前だけをあげると、ローゼンブロック法、 DIRK, MIRK, SIRK, SDIRK といったものがあり、現在盛んに研究されている。
まあ、実用上は、完全陰的なガウスや Radau 公式では問題があるという場合 でなければ、わざわざこれらの方法を使う意味はあまりないように思う。
