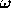天文等で出てくるポアソン方程式の場合には、特にうまく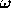 
を決めら
れれば SOR で非常にうまくいくことが多い。が、まあ、世の中はそういう問
題ばかりでもないので、それ以外の方法を紹介だけしておく。
ADI は alternating direction implicit の略である。ここでの基本的な考察 は、「3重対角なら簡単に解ける」ということである。これを使って、 x 方 向と y 方向を交代で解いているうちになんとかなって欲しいというのが ADI の考え方ということになる。
もうちょっとちゃんと書いてみると、例えば j 方向に解くときには、
となる。ここで、 new とつけたのが更新後の値で、これをi=1 から順に解 いていく。 j 方向が終ったら次は i 方向をやる。
ただし、実際に使う上では、 SOR と同じように、修正量の補正をしたほうが 収束が速い。 SOR とは逆に修正量をすこし減らす必要があり、どれくらい減 らすべきかを決めるのにはまたややこしい理屈がいる。
ただし、適当に修正量を決めても最適な SOR よりも遅くはない程度で収束す るという利点がある。
共役勾配法、実は、現在大規模な行列を解くのにはもっとも広く使われている方法 である。これは、特にいろいろな前処理と組み合わせることで、例えば拡散方 程式の定常問題で拡散係数が空間に強く依存する場合にも収束させられ るとか、刻みを場所によって変えるような高度な方法でも同様になんとかでき るとかいう利点があるからである。
しかし、これは安直にプログラムを書いただけではこれまでの紹介してきた方 法に比べて速くなくて、いろいろ高度な変形をして初めて速くなる。また、ほ とんど共役勾配法だけについて議論した良い教科書がいくつもあるので、ここ では省略する。
ポアソン方程式を解く方法の一つで、応用上は重要なのはフーリエ変換を使っ
た方法である。いま、固定境界をやめて周期境界条件でいいことにすると、ポ
アソン方程式の場合、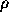 
をフーリエ級数展開して、出てきた係数に
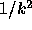(k は波数)を掛けてから逆フーリエ変換すればポアソン方程式の解
になっているわけである。固定境界なら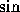 
関数だけで展開すればよい。
フーリエ変換の計算量は多次元でも格子点の総数を n として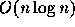 
の程度なので、これは反復法でいうと回数がせいぜい 
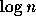で済むという
ことに相当する。
これは極めて強力かつ高速な方法であり、
という条件がすべて満足されていれば、必ずこの方法を使うべきといってもさ しつかえない。
星の構造を解くとかいう場合だと、極座標を使って球面調和関数展開というこ とも多い。この場合の計算には FFT のようなうまい方法があるわけではない （最近高速ルジャンドル変換の研究もあるが、これはよほど項数が大きくない と速くならない）が、r 方向は展開しないで済ませられるのでまあつかえな くはない。
