
一応、今日から講義ということで、今日も少し話をする。まずは放物型偏微分 方程式ということになっているので、そこから。
物理・天文で出てくる偏微分方程式は大抵は 2 階である。で、普通は空間3次 元と時間1次元の4次元空間で定義されるわけだが、この講義ではいくつかの特 殊な場合を除いて空間1次元時間1次元の2次元で考える。 これは、そうしておかないとプログラムを書くのも、また計算機のほうも大変 になるからである。
放物型方程式ってのは何か?というのは皆さん知っているはずなので(だよね?) 厳密な定義は省くが、要するに以下の形に書ける(移流)拡散方程式のことで ある。

ここで x, t はそれぞれ空間、時間を表す変数であり、 u は方程式が 記述する量である。拡散方程式として見ればなにかの濃度ということになるし、 熱伝導の方程式としてみれば温度なりエンタルピーなりということになる。 K は一次の係数で、これは普通の拡散方程式や熱伝導方程式では 0 である。 これが 0 でないのはどういう場合かというのは後でちょっと考える。 D が 普通の拡散係数ということになる。今は D が空間・時間に依存しない場合 を考える。
依存しない場合はもちろん変数分離で解けるので、数値計算することに意味が あるのはD が空間・時間に依存する場合だが、まあ、とりあえずは答がわか る場合を計算してみることにしよう。
放物型方程式の場合には、初期条件と境界条件を与えないと解が定まらない。 以下では、
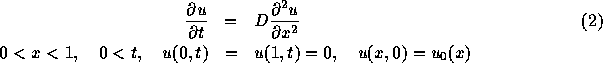
という固定境界の場合を考える。
偏微分方程式の数値計算の方法は基本的には有限要素法と差分法に大別される。 あ、あとスペクトラル法というのもあるが、これはちょっとおいておく。 有限要素法の考え方はだいぶややこしいので、まず差分法を考える。
差分法とは、基本的には微分方程式に出てくる空間微分や時間微分の項を、差 分で置き換えるものである。差分というのはそもそも何かというのを説明 しないといけない。
例えば区間 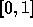 を n等分して、
を n等分して、 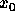 から
から 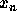 まで
(
まで
(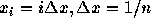 )で表すとする。時間も同様に、
)で表すとする。時間も同様に、 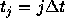 として、これから求める近似解
として、これから求める近似解 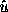 を簡単のため単に
を簡単のため単に
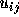 と書く。だいぶ記号が繁雑になるので、図1に
様子を書いておく。
と書く。だいぶ記号が繁雑になるので、図1に
様子を書いておく。
ここで、差分とは例えば 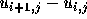 といった具合に隣との差を
とることである。微分を差分で近似するには、例えば
といった具合に隣との差を
とることである。微分を差分で近似するには、例えば
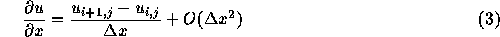
というようなことになる。
なお、差分のとり方は一意的ではないことに注意して欲しい。例えば、
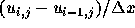 でもいいし、
でもいいし、
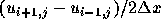 といったものも考えられる。さらに、もっ
と沢山の点を使うことも原理的には可能である。
といったものも考えられる。さらに、もっ
と沢山の点を使うことも原理的には可能である。
さて、拡散方程式なので2次微分がいる。これはどう作ればいいかというわけ だが、これはむしろ一般に高階微分を差分で表す、つまり数値微分の方法を説 明しておくほうが簡単であろう。
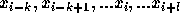 の k+l+1 点での関数値
の k+l+1 点での関数値 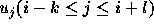 をつかって、点
をつかって、点 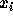 でのm 階導関数の近似値を求める考え方は以下
のようなものである。
でのm 階導関数の近似値を求める考え方は以下
のようなものである。
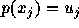 を満たす k+l 次補間多項式
を満たす k+l 次補間多項式 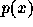 を作る。
を作る。
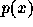 を m 回微分する。
を m 回微分する。
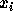 を代入する。
を代入する。
2階導関数を作るためには最低3点いるので、まずもっとも簡単な以下の形を使っ てみる。
で、時間微分についても、もっとも安直な形

を使ってみる。