 |
(17) |
古典力学系のもっとも簡単な例といえば、一次元調和振動子、つまり、運動方
程式では
 |
(17) |
さて、このような、固有値が純虚数である、いいか えれば中立安定な場合、安定性解析はちょっと厄介になる。というのは、通常 の意味で安定というのは、数値解がいつかは原点にいってしまうということ、 いいかえればエネルギーが保存しないということを意味するからである。とい うのは、安定であるとは、線型差分方程式の固有値の絶対値が全て 1 より小 さいということだからである。
つまり、安定領域のある公式では、ほとんどのもので虚軸上の一定範囲では数 値解が「安定」になってしまう。つまり、本当の解はいつまでも振動を続ける のに、数値解は減衰してしまうのである。もちろん、タイムステップを大きく とれば、安定領域から外れるのが普通であり、振動しながら 広がっていくような解になる。安定領域に虚軸を含まないような公式(例えば 前進オイラー公式)の場合では、かならず軌道が広がっていくことになる。つ まり、虚数軸が安定性限界になっていない限り、必ず軌道から一方的に外れて いってしまうのである。
安定領域とはそもそも何かという話をしておく。線形常微分方程式
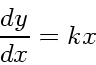 |
(18) |
![]() が複素数の場合も考えるのは、元の微分方程式が連立方程式なら固有値が
実数でない場合もありえるからである。
が複素数の場合も考えるのは、元の微分方程式が連立方程式なら固有値が
実数でない場合もありえるからである。
つまるところ、線形系では安定性限界が虚数軸である(数値解に純虚数の固有 値がある)というのが、数値解が厳密に振動的であるための必要十分条件とい うことになる。この時、数値解はもとの系の性質をある意味で良く表している といえるであろう。
実は多変数の場合や非線形の場合でも本質的な事情は変わらない。ただし、こ ちらはまだいろいろ理論的にはっきりわかっていないことがいろいろある。が、 大雑把にいうと同じような事情が成り立っている。つまり、もとが周期解であ るときに、大抵の積分法では周期解から一方的にずれていく、つまり、保存量 であるはずのエネルギー等が保存しなくなる。
もちろん、エネルギーが厳密には保存しないということが問題であるかどうか というのも実は難しい問題である。というのは、保存しないといってももちろ ん数値解の精度では保存しているわけだから、それでかまわないのではないか とも考えられるからである。
ハミルトン系のシミュレーションの例には例えば以下のようなものがある
これらはいずれも、古典的な多体問題として定式化される。プラズマの場合は
磁場も入るのでちょっと面倒だが、それを無視すれば運動方程式が
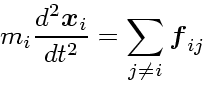 |
(19) |
このような問題に対して、もっとも普通に使われる公式は以下の leapfrog といわれるものである。
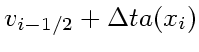 |
(20) | ||
| (21) |
 |
(22) |
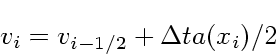 |
(23) |
 |
(24) | ||
![$\displaystyle v_{i} + \Delta t [a(x_i)+a(x_{i+1})]/2$](img74.png) |
(25) |
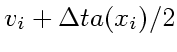 |
(26) | ||
 |
(27) | ||
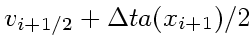 |
(28) |
この公式は局所誤差が 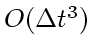 、大域誤差が
、大域誤差が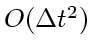 である。
である。
さて、局所誤差という観点からはこれは決して良い公式というわけではないが、 現実にはこの公式は非常に広く使われている。
これは、別にもっとよい方法を知らないからとかではなく、実はこの方法がい くつかの意味で非常に良い方法であるからである。いくつかの意味とは、例え ばエネルギーや角運動量のような保存量が非常によく保存するということであ る。これらの保存量については多くの場合に誤差がある程度以上増えない。
この、ある程度以上誤差が増えないというのは目覚しい性質である。通常の方 法では、エネルギーの誤差は時間に比例して増えていく。従って、長時間計算 をしようとすればそれだけ正確な計算をする必要がある。ところが、エネルギー の誤差は溜っていかないのならば、かならずしも精度を上げる必要はないとも 考えられる。
もちろん、エネルギーが保存していればそれだけで計算が正しいということに はならない。が、理論的には、いくつかの重要な結果が得られている。まず、
Symplectic method については、以下のようなことが知られている
以下、まず数値例でこれらの性質を確認し、それからなぜこのようなうまい性 質を持つのかについて直観的な説明を与えよう(厳密な説明/証明には力学系 の積分可能性に関するかなり深い知識が必要となる)。
能書きを聞いていても良くわからないので、実例を見てみよう。まず、簡単な
例として調和振動子
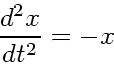 |
(29) |
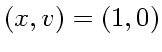 で、時間刻みは
で、時間刻みは 軌道とエネルギーを図に示す。非常に特徴的なのは、 leap frog ではエネル ギーが周期的にしか変化しないのに対し、ルンゲクッタでは単調に増えている ことである。
ルンゲクッタでは単調に変化するというのは前に説明した通り (2階のルンゲクッタでは虚軸を安定領域に含まないため)である。 さて、これに対し、 leapfrog ではエネルギーが変化していないが、これはど ういうことなのであろう?
実は、この調和振動子の場合には、 leapfrog 公式は以下の量
 |
(30) |
 で与えら
れる位相平面の上で考えると、 leapfrog 公式の解は上の式で与えられる楕円
の上にのっているのである。このために、エネルギーの誤差がある値よりも大
きくなり得ないことになる。
で与えら
れる位相平面の上で考えると、 leapfrog 公式の解は上の式で与えられる楕円
の上にのっているのである。このために、エネルギーの誤差がある値よりも大
きくなり得ないことになる。
では、非線形振動ではどうだろう?簡単な例として
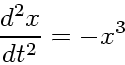 |
(31) |
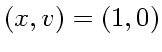 で、時間刻みは
で、時間刻みは 軌道とエネルギーを図に示す。調和振動の場合と同様に、 leap frog ではエネル ギーが周期的にしか変化しないのに対し、ルンゲクッタでは単調に増えている。
この場合も保存量があるので、頑張れば求まるかもしれない。
さて、 leapfrog 公式は、上で見たようにハミルトン系に対してエネルギー誤 差が有界に留まるという大きな特長がある。が、2次精度でしかない。もっと 高次の方法はないのだろうか、またあるとすればどういう原理で作れるのだろ うか。
高次の方法を構成する一つのアプローチが、シンプレクティック公式といわれ るものである。これはなにかというと、積分公式がシンプレクティック写像に なるように作るということである。
シンプレクティック写像とは、ようする に正準変換のことである。正準変換とはなにかというのは解析力学を思い出し てみて欲しいが、直観的には、力学系を不変に保つ、つまり変換まえの座標系で 求めた軌道を変換したものと、変換後の座標系での力学系の軌道が厳密に同じ になるようなものである。
ハミルトン力学系の解そのもの(ある時刻 ![]() での座標から、
での座標から、 ![]() での座
標に移す変換)もシンプレクティックである。まあ、だから、シンプレクティッ
クになっているような積分公式は、そうでないものに比べてなんとなく力学系
の性質にあっているような気はする。
での座
標に移す変換)もシンプレクティックである。まあ、だから、シンプレクティッ
クになっているような積分公式は、そうでないものに比べてなんとなく力学系
の性質にあっているような気はする。
で、いいたかったことは何かっていうと、上の leapfrog 公式はこのシンプレ クティック性を満たしているということだった。詳しくは、「数理科学」 1995年6月号にのった吉田春夫さんによる解説記事でもみてもらうことにして、ここで は高次の公式にはどんなものがあるかという話をしておく。
陽解法の組み立て方はいろいろある。一つは、 RK 系の公式で、係数をシン プレクティック性を満たすように決めるということである。これはここ15年で 無数に論文がでた。4次、あるいは6次の公式としては、吉田や鈴木による作用 素分解に基づく公式が良く知られている。
これらの方法の原理は、要するに上の leap frog をタイムステップを変えて いくつか組合わせるというものである。うまくタイムステップを組み合わせる と誤差の高次の項を消すことができるわけである。3段4次の公式、7段6次の公 式等が吉田によって導かれている。
なお、実は陽解法はハミルトニアンが 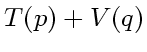 の形の場合にしか使え
ないが、大抵の問題はこう書けることはいうまでもないであろう。
の形の場合にしか使え
ないが、大抵の問題はこう書けることはいうまでもないであろう。
また、 RK 系の公式を力任せに構成する試みもあり、4次から8次までの公式 が作られている。計算精度という観点からはこちらのほうが leapfrog を組合 わせるものよりもいいものもある。
さて、シンプレクティックであるということと、「良い」ということの間には
ちゃんとした理論的な関係があるのであろうか?一応あるということになって
いる。つまり、あるハミルトニアン ![]() で表される系をシンプレクティック
な
で表される系をシンプレクティック
な ![]() 次の公式を使って積分した解は、別のハミルトニアン
次の公式を使って積分した解は、別のハミルトニアン ![]() で与えられ
るシステムの厳密解になっていて、
で与えられ
るシステムの厳密解になっていて、![]() と
と ![]() の間に
の間に
なお、例えば上の調和振動子の場合には実際に数列が収束し、![]() が求まっ
ている。が、これは極めて例外的な場合で、一般の場合には収束するかどうか
も明らかではないようである。
が求まっ
ている。が、これは極めて例外的な場合で、一般の場合には収束するかどうか
も明らかではないようである。
収束するかどうか明らかではないのでは、使っていいことがあるという保証は ないではないかと思うかもしれない。理論的にはその通りなのであるが、実際 にはいろいろな問題に適用されて、従来の方法よりも高い精度が得られるとい うことが確認されている。
さて、式(32) をみるとわかるように、シンプレクティック公式
に付随するハミルトニアン![]() には時間刻み
には時間刻み ![]() が入っている。従って、
が入っている。従って、
![]() をふらふら変えると
をふらふら変えると ![]() も変わって、結果的に求まった数値解は一つの
力学系の軌道ではないなんか変なものになってしまう。ということは、可変時
間刻みにするとシンプレクティック公式はうまく働かないのではないかという
ことが想像される。
も変わって、結果的に求まった数値解は一つの
力学系の軌道ではないなんか変なものになってしまう。ということは、可変時
間刻みにするとシンプレクティック公式はうまく働かないのではないかという
ことが想像される。
じつはその通りで、例えばシンプレクティックで埋め込み型のルンゲクッタと いうものを作って、実際に時間刻みを変えてみた人がいる。その結果、普通の ルンゲクッタよりも良くならないということが発見された (1992年頃)。問題 によってはこれは致命的な欠陥となるので、さまざまな対応法が精力的に研究 されているのが現状である。が、あまり一般的にうまくいく方法というのは見 つかっていないようである。つまり、 万能な公式というのはシンプレクティック公式に関する限り知られていない。
もう一つのシンプレクティック公式の問題点は、「写像」であるということか ら一段法、具体的にはルンゲクッタ型の公式であるので、局所誤差に対する計 算量という観点からは線形多段階法に比べて必ず悪いということである。
これらを解決しようという研究はいろいろあるが、一つの方向が以下に述べる対称型の公式である。
さて、まず対称型公式とはなにかということだが、まず時間反転に対する対称性というものを定義しておこう。時間反
転に対する対称性とは、常微分方程式
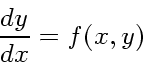 |
(33) |
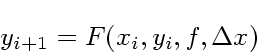 |
(34) |
 |
(35) |
で、一段法の場合には、この意味で対称なものを対称型公式ということにする。
具体例で考えてみよう。例えば前進オイラー法は対称型ではない。これは、いっ た先で導関数を計算すれば、一般にもとのところでの導関数とは違うから当然 であろう。前進オイラー法が対称ではないのだから、その逆写像である後退オ イラー法も対称型ではないことになる。
では、対称型にはどういうものがあるかということだが、明らかに対称型であ るものとしては、台形公式
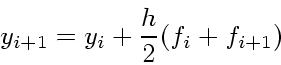 |
(36) |
がある。これが上の対称性を満たしていることはいうまでもない。
さて、なぜこの型の公式を考えるかということであるが、 実験的には以下のようなことが知られている。
前のほうの性質はシンプレクティック公式と同じであるが、後の方の性質はシ ンプレクティック公式よりもある意味でよいものである。
ここではとりあえず対称型公式にはどんなものがあ るかという話をしておこう。
さて、一階の方程式に対する一段法という制限をつけた場合、つまり、ルンゲ
クッタ法の場合、対称な公式はかならず陰的公式になる。逆に、陰的公式であ
れば対称型のものを作るのは容易である。つまり、ルンゲクッタ法を与える行
列 ![]() とかベクトル
とかベクトル ![]() ,
, ![]() が対称になっていればいい。
が対称になっていればいい。
一階の系に対する一段法では、陰的 RK のほかにうまい方法があるわけではな い。それでは、
以下、順番に考えていくことにする。
実は、すでに述べたように、 leapfrog 公式は対称型でありしかも陽公 式である。で、 leapfrog の組合わせで作られる公式も、実は すべて対称型になっている。
線形多段階法でも、対称型というものを考えることはできる。但し、これら の公式は、今のところ
ということが知られており、実用になっていない。これは 国立天文台の福島さんのグループにより精力的に研究が進められている。
一般に対称型というわけではないが、4次の対称型公式を導く特別な方法とし てエルミート型(あるいはエルミート・オブレヒホフ型)と呼ばれる公式のク ラスについてここで触れておこう。
エルミート型公式は、線形多段階法のアダムス型公式の一つの一般化である。 どのような意味において一般化であるかというと、アダムス型と同じように補 間多項式を積分することで新しい時刻での値を求めるところは同じである。違 うところは、アダムス型公式では補間多項式を作るのに関数の値を使う(ラグ ランジュ・ニュートン補間)が、エルミート型公式では、関数の導関数の値も 使うのである(エルミート補間)。
もっとも単純な発想としては、テイラー法というものがある。つまり、微分方
程式
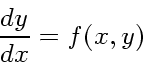 |
(37) |
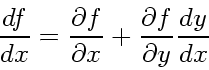 |
(38) |
高次の導関数が簡単に求められる場合(例えば線形な系とか)には、この方法 はかなり強力である。線形多段階法やルンゲクッタに比べて誤差項の係数がずっ と小さく、タイムステップが大きくとれるからである。
が、多くの問題において、高階導関数の直接計算は現実的ではない。これは、
計算量が指数関数的に爆発するのが普通だからである。とはいえ、![]() の一階
導関数や二階導関数くらいならば指数関数的といってもたかがしれている。し
かしながら、これではテイラー法では2次や3次の公式しか作れない。実用的な
公式としては、(leap frog のような特別に良い性質をもっているとかいうの
でなければ)もうちょっと高次のものが必要である。
の一階
導関数や二階導関数くらいならば指数関数的といってもたかがしれている。し
かしながら、これではテイラー法では2次や3次の公式しか作れない。実用的な
公式としては、(leap frog のような特別に良い性質をもっているとかいうの
でなければ)もうちょっと高次のものが必要である。
そこで考えられるのが、高階導関数を使ってさらにルンゲ・クッタ型とか線形
多段階法のような公式を作ることである。例によってもっとも簡単な場合とい
うのを考えると、それは ![]() と
と ![]() のところで
のところで ![]() の一階導関数
の値を使うもの(高次導関数を使わないものであれば台形公式に相当)の一般
化ということになろう。
の一階導関数
の値を使うもの(高次導関数を使わないものであれば台形公式に相当)の一般
化ということになろう。
台形公式は、2次の陰的アダムス型公式と考えることができる。つまり、 ![]() を線
形補間してそれを積分しているわけである。これに対し、
を線
形補間してそれを積分しているわけである。これに対し、 ![]() と
と  を使う補間というのはどういうものかということを考えてみると、こ
れは 3次多項式を構成できることがわかる。具体的には、導関数の近似多項式
を
を使う補間というのはどういうものかということを考えてみると、こ
れは 3次多項式を構成できることがわかる。具体的には、導関数の近似多項式
を
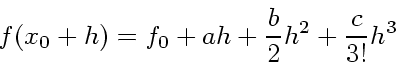 |
(39) |
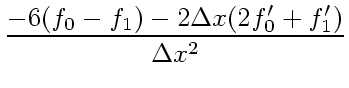 |
|||
 |
(40) |
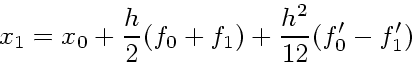 |
(41) |
この公式はプログラムが簡単であるわりには精度が高く、また対称型であるというよ い性質をもつこともあり、良く使われるようになりつつあるようである。収束 させるための反復には普通の直接代入が使える。
対称型一段公式には、対称性を保ったままで時間刻みを変更できるというシン プレクティック公式では(普通の意味では)なかった良い性質がある。以下で は、どのようにしてそれが可能であるかを簡単に述べておく。
今、任意の対称型一段法があって、その時間刻みを与える関数として  が与えられているとする。ここで
が与えられているとする。ここで  はなんでもいいが、これも一段法
である、つまり前のステップの値とかを必要としないものであるとする。
はなんでもいいが、これも一段法
である、つまり前のステップの値とかを必要としないものであるとする。
一般に、  によって刻み幅を決めて求めていった数値解は、時間反転
に対する対称性を満たしていない。つまり、1ステップ積分してから、逆に戻
すと、タイムステップが変わってしまうためにもとのところに戻らない。この
ことのために、例えば周期軌道の場合に誤差が周期的にならないということが
起こるわけである。
によって刻み幅を決めて求めていった数値解は、時間反転
に対する対称性を満たしていない。つまり、1ステップ積分してから、逆に戻
すと、タイムステップが変わってしまうためにもとのところに戻らない。この
ことのために、例えば周期軌道の場合に誤差が周期的にならないということが
起こるわけである。
刻み幅を変えつつ時間反転に対する対称性を保つ一つの方法は(これ以外の方
法もあるかもしれないが、今のところ知られていない)、  自体に対
称性を持たせることである。つまり、一段法を
自体に対
称性を持たせることである。つまり、一段法を
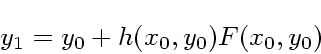 |
(42) |
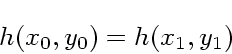 |
(43) |
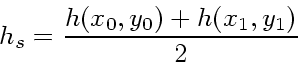 |
(44) |