

Next: 3 現実的な恒星内部構造モデル
Up: 8 常微分方程式の数値解法:境界値問題
Previous: 1 シューティング法
Subsections
Lane-Emden方程式(![[*]](crossref.png) )を境界値問題として解いてみよう。
適当なフィッティングポイント
)を境界値問題として解いてみよう。
適当なフィッティングポイント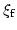 を設け、
中心からフィッティングポイントまでの解は前節で解説した通りの方法で求め、
その解に、表面、即ち
を設け、
中心からフィッティングポイントまでの解は前節で解説した通りの方法で求め、
その解に、表面、即ち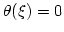 となる
となる
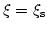 から
積分してきた解が、このフィッティングポイントで一致するようにすれば良い。
から
積分してきた解が、このフィッティングポイントで一致するようにすれば良い。
表面からの積分は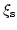 の値を決めた上で行わなければならないのは言うまでもない
が、微分方程式は2階だから、
の値を決めた上で行わなければならないのは言うまでもない
が、微分方程式は2階だから、
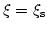 での初期条件が2つ必要である。
その1つは
での初期条件が2つ必要である。
その1つは
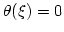 だが、もう1つの
だが、もう1つの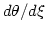 は最初はわからない。
そこで、
は最初はわからない。
そこで、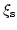 とそこでの
とそこでの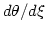 の値をパラメーターとして与えてやれば、
外側の解をこの2つのパラメーターの関数として扱う事が出来る。
の値をパラメーターとして与えてやれば、
外側の解をこの2つのパラメーターの関数として扱う事が出来る。
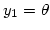 ,
,
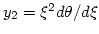 とし、
とし、
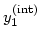 と
と
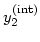 を中心からの積分で求めた
を中心からの積分で求めた
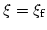 での値、
での値、
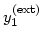 と
と
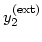 を表面からの積分で求めた
を表面からの積分で求めた
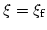 での値としよう。内側の解はユニークに決まっている。
一方、外側の解は
での値としよう。内側の解はユニークに決まっている。
一方、外側の解は
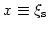 と
そこでの
と
そこでの
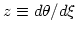 の値に依存している。
全体の解となるには、
の値に依存している。
全体の解となるには、
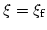 で
で
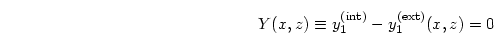 |
(9) |
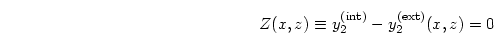 |
(10) |
が満たされなければならない。
手順としては、
先ず、適当に選んだ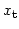 と
と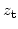 に対する
に対する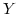 と
と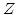 を
求める。
次に、
を
求める。
次に、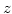 の値を変えずに、
の値を変えずに、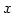 を
を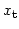 から
から
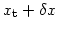 に変えて、
に変えて、
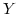 及び
及び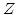 の変化量を求める。
同様に、
の変化量を求める。
同様に、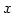 の値を変えずに、
の値を変えずに、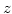 を
を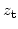 から
から
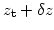 に変えて、
に変えて、
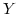 及び
及び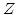 の変化量を求める。
これから
の変化量を求める。
これから
![\begin{displaymath}
\partial Y/\partial x =
[Y(x_{\rm t}+\delta x,z_{\rm t})-Y(x_{\rm t},z_{\rm t})]/\delta x
\end{displaymath}](img49.png) |
(11) |
![\begin{displaymath}
\partial Y/\partial z =
[Y(x_{\rm t},z_{\rm t}+\delta z)-Y(x_{\rm t},z_{\rm t})]/\delta z
\end{displaymath}](img50.png) |
(12) |
を数値的に求める。
今、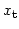 、
、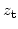 の値が、真の解
の値が、真の解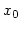 ,
,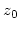 から
から
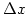 ,
,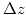 ずれているとすると、1次の精度で、
ずれているとすると、1次の精度で、
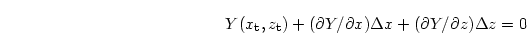 |
(13) |
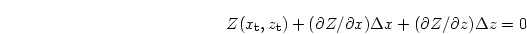 |
(14) |
となる。そこで、上の2式から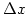 と
と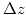 を求め、
を求め、
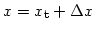 を改めて
を改めて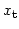 ,
,
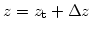 を改めて
を改めて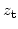 として、
として、
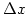 ,
,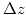 が充分小さくなるまで、逐次計算を繰り返せば良い。
が充分小さくなるまで、逐次計算を繰り返せば良い。
境界値問題として、Lane-Emden方程式を解け。
Jun Makino
平成15年6月5日
![[*]](crossref.png) )を境界値問題として解いてみよう。
適当なフィッティングポイント
)を境界値問題として解いてみよう。
適当なフィッティングポイント![]() の値を決めた上で行わなければならないのは言うまでもない
が、微分方程式は2階だから、
の値を決めた上で行わなければならないのは言うまでもない
が、微分方程式は2階だから、
![]() での初期条件が2つ必要である。
その1つは
での初期条件が2つ必要である。
その1つは
![]() だが、もう1つの
だが、もう1つの![]() は最初はわからない。
そこで、
は最初はわからない。
そこで、![]() とそこでの
とそこでの![]() の値をパラメーターとして与えてやれば、
外側の解をこの2つのパラメーターの関数として扱う事が出来る。
の値をパラメーターとして与えてやれば、
外側の解をこの2つのパラメーターの関数として扱う事が出来る。
![]() ,
,
![]() とし、
とし、
![]() と
と
![]() を中心からの積分で求めた
を中心からの積分で求めた
![]() での値、
での値、
![]() と
と
![]() を表面からの積分で求めた
を表面からの積分で求めた
![]() での値としよう。内側の解はユニークに決まっている。
一方、外側の解は
での値としよう。内側の解はユニークに決まっている。
一方、外側の解は
![]() と
そこでの
と
そこでの
![]() の値に依存している。
全体の解となるには、
の値に依存している。
全体の解となるには、
![]() で
で
![]() と
と![]() に対する
に対する![]() と
と![]() を
求める。
次に、
を
求める。
次に、![]() の値を変えずに、
の値を変えずに、![]() を
を![]() から
から
![]() に変えて、
に変えて、
![]() 及び
及び![]() の変化量を求める。
同様に、
の変化量を求める。
同様に、![]() の値を変えずに、
の値を変えずに、![]() を
を![]() から
から
![]() に変えて、
に変えて、
![]() 及び
及び![]() の変化量を求める。
これから
の変化量を求める。
これから