

Next: 2 二分法
Up: 6 方程式の数値解法
Previous: 6 方程式の数値解法
Subsections
Newton-Raphson法は、関数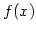 が単調連続で変曲点がなく、且つ導関数
が単調連続で変曲点がなく、且つ導関数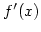 が
数値的に求められる時に利用できる数値解法で、収束が速く、広く用いられている。
いま、曲線上の点
が
数値的に求められる時に利用できる数値解法で、収束が速く、広く用いられている。
いま、曲線上の点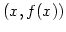 での接線と
での接線と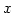 -軸との交点を
-軸との交点を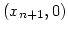 とすると、
とすると、
 |
(1) |
だから、
解の適当な推定値から始めて、反復公式
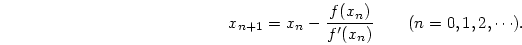 |
(2) |
を繰り返すと、
漸近的に解に達する。
Figure 6.1:
Newton-Raphson法の概念図。
 |
収束の判定条件としては、ある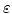 に対して、
に対して、
- 二つの近似解間の差
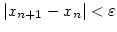
- 二つの近似解間の相対差
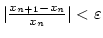
- 二つの近似解関数値間の差
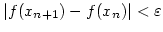
等が考えられるが、1と2の条件では、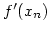 の値が大きいと、真の解に未だ
充分近くないのに満たされてしまう場合があるので、3の条件を判定条件として用いる
方が誤った解を出してしまう危険性がすくない。
の値が大きいと、真の解に未だ
充分近くないのに満たされてしまう場合があるので、3の条件を判定条件として用いる
方が誤った解を出してしまう危険性がすくない。
以下の外部関数rtnewtは、関数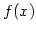 をfuncdとして、
をfuncdとして、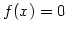 となる解を
Newton-Raphson法で解くプログラム例である
となる解を
Newton-Raphson法で解くプログラム例である
![[*]](footnote.png) 。収束判定条件は上記1を使っている。
。収束判定条件は上記1を使っている。
function rtnewt(funcd,x1,x2,xacc)
Implicit NONE
Integer JMAX
Real rtnewt,x1,x2,xacc
external funcd
Parameter (JMAX=20) !Set to maximum number of iterations.
! Using the Newton-Raphson method, find the root of a function known to
! lie in the interval [x1,x2]. The root 'rtnewt' will be refined until
! its accuracy is known within +-'xacc'. 'funcd' is a user-supplied
! subroutine that returns both the function value and the first
! derivative of the function at the point x.
Integer j
Real df,dx,f
rtnewt=.5*(x1+x2) !Initial guess.
do j=1,JMAX
call funcd(rtnewt,f,df)
dx=f/df
rtnewt=rtnewt-dx
if((x1-rtnewt)*(rtnewt-x2).lt.0.)
* pause 'rtnewt jumped out of brackets'
if(abs(dx).lt.xacc) return !Convergence.
end do
pause 'rtnewt exceeded maximum iterations'
end
上記サンプルプログラムで、external funcdという行がある。これは、
EXTERNAL文と呼ばれる宣言文である。FUNCTION文の引数は、通常はその関数の独立変
数であるが、今の場合、funcdは、解きたい関数名である。そして、
この関数は、別にサブルーチンで与える。そこで、
FUNCTION文の引数が、外部手続きサブルーチンの名である事を宣言しておくのである。
Newton-Raphson法で、
 |
(3) |
を解け。
CfA カタログを使って、銀河の天球上の
赤経・赤緯座標、銀経・銀緯座標、の二次元マップを、
Mollwide画法で描いて見よう。
Mollwide図法では経度・緯度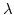 -
-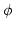 を次の様に
を次の様に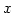 -
-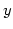 座標に変換する。
座標に変換する。
 |
(4) |
 |
(5) |
但し、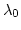 は地図上の中心経度であり、
は地図上の中心経度であり、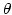 は
は
 |
(6) |
で定義する
![[*]](footnote.png) 。
(経度
。
(経度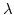 はファイルGALAXY.DATから読み取った値を直接使用するのではない。
適切な変換をしてから使用する。
図6.2、6.3の
はファイルGALAXY.DATから読み取った値を直接使用するのではない。
適切な変換をしてから使用する。
図6.2、6.3の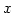 -軸を見て、良く考えよう。)
与えられた緯度
-軸を見て、良く考えよう。)
与えられた緯度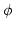 から上の式に基づいて
から上の式に基づいて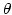 を求めるには、
先ず適当な推定値
を求めるには、
先ず適当な推定値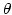 を用意して、
Newton-Raphson法により、上の式を満たすように逐次修正して行けば良い。
修正値
を用意して、
Newton-Raphson法により、上の式を満たすように逐次修正して行けば良い。
修正値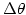 は、(6.2)式を使って、
は、(6.2)式を使って、
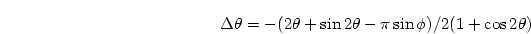 |
(7) |
で求め、これを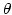 に加えたものを改めて
に加えたものを改めて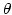 として、
修正値
として、
修正値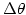 が予め定めておいた限界値以下になるまで、
上のプロセスを繰り返す。
が予め定めておいた限界値以下になるまで、
上のプロセスを繰り返す。
Figure 6.2:
銀河の天球上の分布。赤経、赤緯座標で図示。
 |
赤経(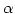 )・赤緯(
)・赤緯(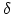 )と銀経(
)と銀経(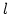 )・銀緯(
)・銀緯(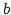 )の変換は、
銀河の北極の赤経・赤緯を
)の変換は、
銀河の北極の赤経・赤緯を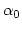 ,
,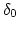 とし、
とし、
 |
(8) |
 |
(9) |
 |
(10) |
として、
 |
(11) |
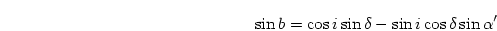 |
(12) |
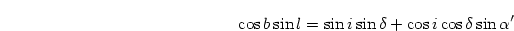 |
(13) |
で与えられる。但し、
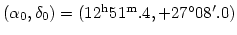 。
。
Figure 6.3:
銀河の天球上の分布。銀経、銀緯座標で図示。
 |


Next: 2 二分法
Up: 6 方程式の数値解法
Previous: 6 方程式の数値解法
Jun Makino
平成15年5月29日
![]() に対して、
に対して、
![]() をfuncdとして、
をfuncdとして、![]() となる解を
Newton-Raphson法で解くプログラム例である
となる解を
Newton-Raphson法で解くプログラム例である
![[*]](footnote.png) 。収束判定条件は上記1を使っている。
。収束判定条件は上記1を使っている。
![]() -
-![]() を次の様に
を次の様に![]() -
-![]() 座標に変換する。
座標に変換する。
![[*]](footnote.png) 。
(経度
。
(経度![]() )・赤緯(
)・赤緯(![]() )と銀経(
)と銀経(![]() )・銀緯(
)・銀緯(![]() )の変換は、
銀河の北極の赤経・赤緯を
)の変換は、
銀河の北極の赤経・赤緯を![]() ,
,![]() とし、
とし、