Next: 6 問題:境界値問題の例
Up: 10 レポート問題
Previous: 4 問題:Runge-Kutta法とEuler法と修正Euler法
- 指数
 、
、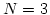 、及び
、及び 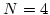 の場合について、Lane-Emden equation を Runge-Kutta 法を用いて数値的に解け。
の場合について、Lane-Emden equation を Runge-Kutta 法を用いて数値的に解け。
- 太陽が
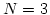 のポリトロープで近似できるとして、その内部構造を求めよ。
但し太陽半径
のポリトロープで近似できるとして、その内部構造を求めよ。
但し太陽半径
 km、
太陽質量
km、
太陽質量
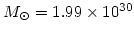 kg
とし、内部は完全気体の状態方程式
kg
とし、内部は完全気体の状態方程式
 |
(367) |
に従うものとする。
ここで は単位体積当たりの全粒子数、
は単位体積当たりの全粒子数、 はボルツマン定数。
今、水素、ヘリウム、それ以外の元素が質量比
はボルツマン定数。
今、水素、ヘリウム、それ以外の元素が質量比 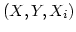 である
完全電離理想気体を考える。水素原子の質量を
である
完全電離理想気体を考える。水素原子の質量を 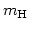 で表わすとすると、
水素については核の数密度は
で表わすとすると、
水素については核の数密度は
 、電子の数密度は同じく
、電子の数密度は同じく
 、ヘリウムについては核の数密度は
、ヘリウムについては核の数密度は
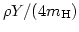 、
電子の数密度は
、
電子の数密度は
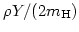 、それら以外の元素については、それぞれの
元素の atomic weight を
、それら以外の元素については、それぞれの
元素の atomic weight を 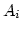 、atomic number を
、atomic number を 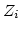 とすると、
核の数密度は
とすると、
核の数密度は
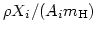 、
電子の数密度は
、
電子の数密度は
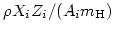 だから、
全粒子数
だから、
全粒子数  は
は
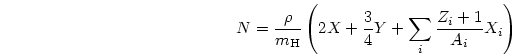 |
(368) |
となる。
重元素については
 だから、
水素とヘリウム以外の元素の質量比を
だから、
水素とヘリウム以外の元素の質量比を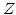
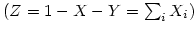 と表わす事にすれば、
と表わす事にすれば、
 |
(369) |
であり、ガス圧は
ここに は
は
 |
(372) |
で、平均分子量と呼ぶ。また
 J
J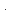 kg
kg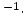 K
K 。
(
。
(
 J
J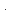 K
K 、
、
 kg)。
太陽の水素、ヘリウム、金属の質量比はそれぞれ
kg)。
太陽の水素、ヘリウム、金属の質量比はそれぞれ
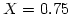 、
、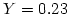 、
、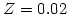 とする。
とする。
Jun Makino
平成15年4月17日