



Next: 2 固有値問題としてのLane-Emden 方程式
Up: 9 常微分方程式の数値解法:固有値問題
Previous: 9 常微分方程式の数値解法:固有値問題
Subsections
境界値問題の中でも固有値問題は様々な物理的問題で登場する。
古典物理の問題での弦の振動の問題や、量子力学の(定常状態に対する)
Schrödinger方程式を思い浮かべれば、その事は明らかであろう。
波動方程式
 |
(247) |
を、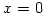 で
で ,
,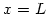 で
で という条件の下に解く事を考える。
適当な固有値
という条件の下に解く事を考える。
適当な固有値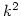 を仮定すると、この問題は前のセクションで扱った境界値問題とし
て扱う事が出来る。すなわち、
を仮定すると、この問題は前のセクションで扱った境界値問題とし
て扱う事が出来る。すなわち、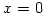 での
での 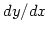 を与えて、
を与えて、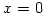 から
から
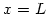 まで、初期値問題として積分していき、
まで、初期値問題として積分していき、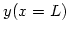 が
が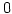 になるかどうかを見れば
良い。
任意の
になるかどうかを見れば
良い。
任意の 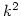 に対して、
に対して、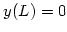 は満たされず、特定の
は満たされず、特定の 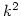 の値の場合のみ、
の値の場合のみ、
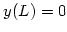 が満たされる。
丁度
が満たされる。
丁度 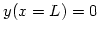 を満たすとき、その仮定した
を満たすとき、その仮定した 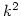 は固有値であり、解
は固有値であり、解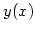 が
固有関数である。
固有値問題では、解の形は固有解としてユニークに決まるが、解の絶対値は
不定なので規格化の自由度が残る。
が
固有関数である。
固有値問題では、解の形は固有解としてユニークに決まるが、解の絶対値は
不定なので規格化の自由度が残る。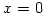 での
での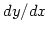 を自由に与える事は、
規格化を自由にしている事に対応する。
を自由に与える事は、
規格化を自由にしている事に対応する。
 |
(248) |
を、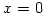 で
で ,
, で
で という条件の下に数値的に解け。
という条件の下に数値的に解け。
Jun Makino
平成15年4月17日