


Next: 2 Theory
Up: No Title
Previous: No Title
It is generally accepted that [the] terrestrial planets and the cores
of [the] Jovian planets are [are  were] formed through the accretion
of many small bodies called planetesimals. The accretion process is
rather complex, since several competing physical mechanisms are
working simultaneously
Lissauer1993see e.g.. In particular, the interplay of
the velocity distribution and the mass distribution is quite
complex.
were] formed through the accretion
of many small bodies called planetesimals. The accretion process is
rather complex, since several competing physical mechanisms are
working simultaneously
Lissauer1993see e.g.. In particular, the interplay of
the velocity distribution and the mass distribution is quite
complex.
There had [had  have] been several numerical studies of [the]
accretion process, in which the coupling between the evolution of the
velocity distribution and the mass distribution was taken into
account. The importance of the coupling was first pointed out by
Greenberg1978. WetherillStewart1989
used the ``particle-in-a-box'' approach with various assumptions for
the velocity distribution to study the coupling. They found the
[delete ``the''] ``runaway growth'' of massive planetesimals in the
simulations which included the effect of the energy equipartition.
have] been several numerical studies of [the]
accretion process, in which the coupling between the evolution of the
velocity distribution and the mass distribution was taken into
account. The importance of the coupling was first pointed out by
Greenberg1978. WetherillStewart1989
used the ``particle-in-a-box'' approach with various assumptions for
the velocity distribution to study the coupling. They found the
[delete ``the''] ``runaway growth'' of massive planetesimals in the
simulations which included the effect of the energy equipartition.
KokuboIda1996 performed full three-dimensional N-body
simulations of the planetary accretion process, and confirmed that the
[delete ``the''] runaway growth takes place. They also found that the
mass distribution first relaxes to the power-law form
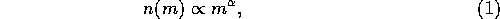
with 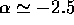 , for the mass range covered by their
calculation (
, for the mass range covered by their
calculation (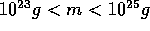 ). Here,
). Here, 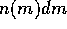 gives the surface number density of planetesimals with the [delete
``the''] mass between m and m + dm. Earlier studies based on more
approximate theory (Wetherill and Stewart 1989, 1993, Barge and Pellat
1991, 1993) also showed similar results for that mass range. On the
other hand, in the case of two-dimensional simulation[s], no simple
power-law mass distribution was realized.
gives the surface number density of planetesimals with the [delete
``the''] mass between m and m + dm. Earlier studies based on more
approximate theory (Wetherill and Stewart 1989, 1993, Barge and Pellat
1991, 1993) also showed similar results for that mass range. On the
other hand, in the case of two-dimensional simulation[s], no simple
power-law mass distribution was realized.
It should be noted that this range of the [delete ``the''] mass
contains most of the mass when the runaway takes place. For the mass
[``the mass''  ``masses''] less than
``masses''] less than 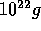 , planetesimals
exhibit orderly growth, because the condition for the run[a]way is not
satisfied
OhtsukiIda1990 e.g..
, planetesimals
exhibit orderly growth, because the condition for the run[a]way is not
satisfied
OhtsukiIda1990 e.g..
In addition, this power-law mass distribution is realized almost
immediately once the run[a]way starts. Therefore, the same mechanism
which drives the runaway growth should be responsible for this power
law mass distribution. However, no theoretical explanation has been
proposed yet.
In this paper, we present an exact stationary solution of the
coagulation equation which explains why the power-law mass
distribution is realized in the early stage of the accretion
process. In section 2, we derive the exact stationary solution of the
coagulation equation. In section 3[,] we present a more intuitive
description of the mechanism of the formation of the power-law
distribution. In section 4, we discuss the implication[s] of our result.



Next: 2 Theory
Up: No Title
Previous: No Title
Jun Makino
Fri Jun 19 21:16:46 JST 1998
 were] formed through the accretion
of many small bodies called planetesimals. The accretion process is
rather complex, since several competing physical mechanisms are
working simultaneously
Lissauer1993see e.g.. In particular, the interplay of
the velocity distribution and the mass distribution is quite
complex.
were] formed through the accretion
of many small bodies called planetesimals. The accretion process is
rather complex, since several competing physical mechanisms are
working simultaneously
Lissauer1993see e.g.. In particular, the interplay of
the velocity distribution and the mass distribution is quite
complex.
 have] been several numerical studies of [the]
accretion process, in which the coupling between the evolution of the
velocity distribution and the mass distribution was taken into
account. The importance of the coupling was first pointed out by
Greenberg1978. WetherillStewart1989
used the ``particle-in-a-box'' approach with various assumptions for
the velocity distribution to study the coupling. They found the
[delete ``the''] ``runaway growth'' of massive planetesimals in the
simulations which included the effect of the energy equipartition.
have] been several numerical studies of [the]
accretion process, in which the coupling between the evolution of the
velocity distribution and the mass distribution was taken into
account. The importance of the coupling was first pointed out by
Greenberg1978. WetherillStewart1989
used the ``particle-in-a-box'' approach with various assumptions for
the velocity distribution to study the coupling. They found the
[delete ``the''] ``runaway growth'' of massive planetesimals in the
simulations which included the effect of the energy equipartition.
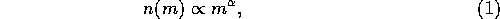
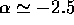 , for the mass range covered by their
calculation (
, for the mass range covered by their
calculation (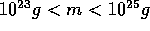 ). Here,
). Here, 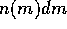 gives the surface number density of planetesimals with the [delete
``the''] mass between m and m + dm. Earlier studies based on more
approximate theory (Wetherill and Stewart 1989, 1993, Barge and Pellat
1991, 1993) also showed similar results for that mass range. On the
other hand, in the case of two-dimensional simulation[s], no simple
power-law mass distribution was realized.
gives the surface number density of planetesimals with the [delete
``the''] mass between m and m + dm. Earlier studies based on more
approximate theory (Wetherill and Stewart 1989, 1993, Barge and Pellat
1991, 1993) also showed similar results for that mass range. On the
other hand, in the case of two-dimensional simulation[s], no simple
power-law mass distribution was realized.
 ``masses''] less than
``masses''] less than 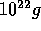 , planetesimals
exhibit orderly growth, because the condition for the run[a]way is not
satisfied
OhtsukiIda1990 e.g..
, planetesimals
exhibit orderly growth, because the condition for the run[a]way is not
satisfied
OhtsukiIda1990 e.g..