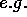 , [vv98]) and large
interferometer arrays (
, [vv98]) and large
interferometer arrays (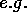 , [MMH+95]) have shown that
many galaxies host central massive objects with a mass million
or even billion times larger than that of the mass of our sun.
, [MMH+95]) have shown that
many galaxies host central massive objects with a mass million
or even billion times larger than that of the mass of our sun.
The structure and dynamics of the central region of galaxies is an
important field of research in astrophysics. Of particular interest is the
existence of massive black holes. Observations using the Hubble Space
Telescope (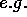 , [vv98]) and large
interferometer arrays (
, [vv98]) and large
interferometer arrays (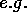 , [MMH+95]) have shown that
many galaxies host central massive objects with a mass million
or even billion times larger than that of the mass of our sun.
, [MMH+95]) have shown that
many galaxies host central massive objects with a mass million
or even billion times larger than that of the mass of our sun.
The most direct observational evidence for the existence of a massive
black hole is for the presence of a black hole in the very core of
our own galaxy
[EOG99]. Here, thanks to our close proximity, observers can
now see individual stars with a distance of less than 0.01 parsecs from
the central massive object and measure their radial (line of sight)
velocities as well as tangential velocities (through proper motion
measurements). All evidence is quite consistent with the existence
of a massive black hole with a mass of 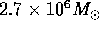 (here
(here  is one solar mass) at the center of the galaxy.
is one solar mass) at the center of the galaxy.
The evidence for the existence of black holes in distant galaxies is less direct. Nonetheless, there is now little doubt that most galaxies host massive central objects, which are most likely massive black holes. Among these massive black holes, those in large elliptical galaxies are known to be the most massive. The mass of black holes in normal spiral galaxies is typically several million solar masses. The mass of black holes in elliptical galaxies is much larger, typically more than a hundred million solar masses.
How are such massive black holes formed? How is their formation process related to the formation process of the galaxy itself? Why do elliptical galaxies have more massive black holes than spiral galaxies? In order to answer these questions, we need to interpret observations with the help of numerical experiments (simulations).
The standard theory of the formation of elliptical galaxies is that they are formed through merging of smaller galaxies, either spiral galaxies or elliptical galaxies [TT72]. Numerical simulations of galaxy merging have demonstrated that this theory explains many observed features of elliptical galaxies very well.
When two spiral galaxies merge, the gas in the disk of a galaxy is strongly perturbed by the gravitational force from the other galaxy, and tends to concentrate into the central region of the galaxy well before two galaxies actually merge. Such a high-density gas results in very high star forming activity, which is observed in many interacting galaxies. Also, some of the gas would eventually be absorbed by the central black hole.
Thus, when two galaxies finally merge, the black holes have become much more massive than their original mass, and most of the gas in the galaxies is lost. These black holes will settle in the center of the merger galaxy, through the dynamical friction from other stars in the galaxy. In other words, the galaxy that is the product of the merger of two galaxies is likely to have two black holes in the center. What will happen to these two black holes?
These black holes form a bounded pair (binary), and the binding energy of the binary increases over time through dynamical friction. If the dynamical friction remains effective until the separation of the two black holes in the binary becomes small enough for the gravitational radiation to shrink the separation further, the two black holes will merge. Such mergings of two massive black holes would emit strong gravitational wave which will be observable through space-based gravitational wave detectors such as LISA [JCR94].
However, N-body simulations of the evolution of binary black holes in the center of a galaxy [ME96,Qui96,Mak97,QH97] have suggested a different picture. Before the separation of the black holes becomes small enough, the binary black hole expels almost all the stars in its vicinity, resulting in a region devoid of stars. As a result, dynamical friction from field stars becomes inefficient.
N-body simulations of binary black holes in the center of
the galaxy pose numerically very tough problems. There are several
reasons why these are tough. In order to obtain a
reliable result, we need to use as many particles (stars) as possible,
to reduce the numerical relaxation effects. Here, numerical relaxation
denotes the effect that stars change their velocity randomly through
encounters with other stars. The strength of this effect is
proportional to 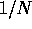 , where N is the number of stars in the
system. In the limit of
, where N is the number of stars in the
system. In the limit of 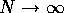 ,
this effect becomes zero. In real galaxies, this effect exists, but
is very small. In numerical simulations with, say,
,
this effect becomes zero. In real galaxies, this effect exists, but
is very small. In numerical simulations with, say, 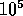 stars, this
effect is several orders of magnitude larger than that in real
galaxies.
stars, this
effect is several orders of magnitude larger than that in real
galaxies.
Another reason is that the simulation should cover a very wide range
in timescales. Typical stars in a galaxy have orbital timescales
of 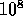 years, and therefore the timestep necessary to integrate the
orbit of these stars accurately
is around
years, and therefore the timestep necessary to integrate the
orbit of these stars accurately
is around 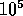 years. The orbital period of the black hole binary
can be anywhere between
years. The orbital period of the black hole binary
can be anywhere between 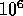 years and 10 minutes. Of course, we do
not need to follow a binary with an orbital period of 10 minutes
for a long time, since the black holes would merge in a few orbital periods
anyway. However, in order to see if
gravitational radiation becomes effective or not, we need to
follow binaries with an orbital period of about one
year. Thus, it is crucial to assign different timesteps to different
stars (using individual timestep algorithms, [1]).
years and 10 minutes. Of course, we do
not need to follow a binary with an orbital period of 10 minutes
for a long time, since the black holes would merge in a few orbital periods
anyway. However, in order to see if
gravitational radiation becomes effective or not, we need to
follow binaries with an orbital period of about one
year. Thus, it is crucial to assign different timesteps to different
stars (using individual timestep algorithms, [1]).
This requirement to handle a wide range of the timescales leads to the additional requirement of very high accuracy, simply because black holes and stars close to black holes are integrated for a very large number of orbits. The gravitational forces on particles should be calculated to high accuracy. The orbits should also be integrated with high accuracy.
These two requirements of a wide range in timescales and high accuracy makes the numerical simulation very difficult. In particular, no one has succeeded to use the tree algorithm for this kind of problem. The tree algorithm is now widely used for simulations of the formation and evolution of galaxy clusters, galaxy groups and individual galaxies. However, in these calculations the central regions of galaxies are not correctly modeled.
It is not impossible to combine the individual timestep approach with a tree algorithm [MA93], and achieve high accuracy at the same time. However, in order to obtain astrophysically useful results from such a code, parallelization is necessary in order to obtain high calculation speeds, and that poses a difficult problem.
In fact, even without tree algorithm, the implementation of the individual timestep algorithm on massively parallel computers turned out to be indeed a difficult problem. The reason is that we need a very low-latency network which can perform broadcast or global reduction, or preferably both. The fraction of the stars with very small timestep is small, but since they have such small timesteps, a large fraction of the total calculation time is spent to obtain gravitational forces on them. So we have to efficiently parallelize the calculation of the force on a small number of particles. One can get good performance on vector processors, shared-memory multiprocessors, and small-scale distributed-memory parallel computers with a very low-latency network, but with present large MPPs, it's very difficult to achieve good performance.
Black holes in the center of a galaxy form just one example of tough problems in astrophysics. Many astrophysical systems share the same characteristic of exhibiting a wide range in timescales. This problem arises directly from the fact that the gravitational force is an attractive force with no characteristic scale length.
In order to accelerate N-body simulations with individual timestep algorithms, we have developed a series of special-purpose hardwares for the force calculation [4,MT98]. The direct force calculation is well suited for acceleration by specialized hardware, because of its simplicity. The use of individual timesteps adds extra complexity to the hardware and software, but still we can achieve pretty high performance. In the case of special-purpose computers, it is not too difficult to implement a fast network for broadcast and reduction. So the latency problem of general-purpose massively parallel computers is solved by hardware.
It should be noted that the use of GRAPE hardware is not limited to direct summation. GRAPE can achieve pretty high performance for the tree algorithm, as demonstrated by our entry for the Gordon Bell prize last year.
In 1995, we completed GRAPE-4[MTES97] with a peak speed of 1.08 Tflops. The direct N-body simulations on this system were awarded the Gordon Bell prize in 1995 (112 Gflops) and 1996 (333Gflops). In 1997, we started the development of the GRAPE-6 system. The full GRAPE-6 system will be completed by year 2001, and will achieve a peak speed of 100 Tflops. In this paper, we report the performance of 1/48 of the total system, which is currently up and running as a testbed. In section 2, we describe the GRAPE-6 system and its present status. In section 3, we report the simulation performed on GRAPE-6.