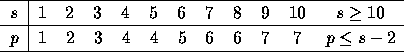
理論的、あるいは実用上重要なのは、段数を決めた時に、次数がいくつまで可 能かということである。が、これは一般の場合には未解決であり、以下の結果 しかわかっていない
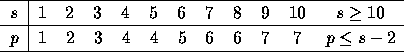
ある段数で、到達可能な最高次数を達成する公式というのは一通りではない。 2段2次の場合でも、自由パラメータが一つあって「無限個」の公式があり得る わけである。段数が増えれば自由パラメータの数も増える。
それではどういう公式を使うべきかというのは、精力的な研究が行なわれてき た。問題にもよるが、例えば
Dormand と Prince は、最近、段数/次数のさまざまな組合せについて、局所 離散化誤差を非常に小さくした公式を求めた。