 には時間刻み h が入っている。従って、
h をふらふら変えると
には時間刻み h が入っている。従って、
h をふらふら変えると 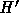 も変わって、結果的に求まった数値解は一つの
力学系の軌道ではないなんか変なものになってしまう。ということは、可変時
間刻みにするとシンプレクティック公式はうまく働かないのではないかという
ことが想像される。
も変わって、結果的に求まった数値解は一つの
力学系の軌道ではないなんか変なものになってしまう。ということは、可変時
間刻みにするとシンプレクティック公式はうまく働かないのではないかという
ことが想像される。
さて、式(14) をみるとわかるように、シンプレクティック公式
に付随するハミルトニアン には時間刻み h が入っている。従って、
h をふらふら変えると
には時間刻み h が入っている。従って、
h をふらふら変えると 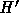 も変わって、結果的に求まった数値解は一つの
力学系の軌道ではないなんか変なものになってしまう。ということは、可変時
間刻みにするとシンプレクティック公式はうまく働かないのではないかという
ことが想像される。
も変わって、結果的に求まった数値解は一つの
力学系の軌道ではないなんか変なものになってしまう。ということは、可変時
間刻みにするとシンプレクティック公式はうまく働かないのではないかという
ことが想像される。
じつはその通りで、例えばシンプレクティックで埋め込み型のルンゲクッタと いうものを作って、実際に時間刻みを変えてみた人がいる。その結果、普通の ルンゲクッタよりも良くならないということが発見された (1992年頃)。問題 によってはこれは致命的な欠陥となるので、さまざまな対応法が精力的に研究 されているのが現状である。が、あまり一般的にうまくいく方法というのは見 つかっていないようである。つまり、 stiff な問題の場合にあったような、 万能な公式というのはシンプレクティック公式に関する限り知られていない。
なお、シンプレクティック公式において普通に時間刻みを変えると、それはシ ンプレクティックではなくなるということが Gear と Skeel により一般に証 明されている。彼らの結果は、時間刻みも含めて考えると、写像が時間方向に 歪んだもの(もとの位置によって時間刻みが変わるため)になり、そのために 元の公式がシンプレクティックであれば時間刻みを変えると必ずシンプレクティッ クでなくなるというものである。
それでは、時間刻みを変えるのは絶対に不可能かというと、以下のような考え かたでの研究が進められている。ハミルトニアン H を

と複数の項の和にわけ、それぞれについて違う時間刻みを与えることで実効的 に時間刻みを変えるというものである。これについては来週か再来週にもう少 し詳しく触れることにしたい。
もう一つのシンプレクティック公式の問題点は、「写像」であるということか ら一段法、具体的にはルンゲクッタ型の公式であるので、局所誤差に対する計 算量という観点からは線形多段階法に比べて必ず悪いということである。
一般に多段階法についてシンプレクティック性のようなものがありえるかどう かというのは、現在研究が進みつつあるが良くわかっていない。