 と、別の刻み幅
と、別の刻み幅 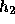 で計算した答の誤差は、
それぞれ、ある(共通の)定数 C を使って
で計算した答の誤差は、
それぞれ、ある(共通の)定数 C を使って
今日は、数値解の公式の最後ということで、外挿法について紹介する。まず、 そのための準備として、密接に関係した数値積分における外挿の考え方を説明 し、それから常微分方程式の数値解法としての補外法についてその考え方を説 明する。
陰的ルンゲ・クッタとガウス・ルジャンドル多項式による数値積分の関係にみ るように、数値積分と常微分方程式の数値解法には密接な関係がある。理論的 には、これは結局リプシッツ条件のもとで、常微分方程式の数値解は数値積分 で近似できるということから来る。
線形多段階法も、多項式近似した上で数値積分する方法というふうに理解でき る。このような方法で非常に高い次数を達成しようとすると、計算量、メモリ の必要量がどんどん増えてしまって現実的ではなくなる。また、あとで述べる ように安定性や収束性の問題もおきてきて、非常に高次の方法というのはかな らずしも実用的ではない。
では、もう少しうまい方法はないかというのが問題である。
例えば、数値積分において、簡単な台形公式を使った場合を考えてみる。これ で刻み幅をいろいろ変えれば、誤差は大雑把にいって刻み幅 h の2乗に比例 するはずである。
つまり、例えばある刻み幅  と、別の刻み幅
と、別の刻み幅 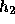 で計算した答の誤差は、
それぞれ、ある(共通の)定数 C を使って
で計算した答の誤差は、
それぞれ、ある(共通の)定数 C を使って

と書けるような気がする。これをさらに言い換えると、積分の近似値  が、真の値 S を使って
が、真の値 S を使って

さて、この式から、「Sを求める」ことが出来る。つまり、

としてやると、「真の値」が求まってしまう。
図にするとこんな感じかな:

要するに、 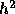 に対して誤差が一次式で書けると信じて、
に対して誤差が一次式で書けると信じて、  での積分の値を求めてやるわけである。
での積分の値を求めてやるわけである。
もちろん、これで本当の真の値が求まるわけではない。というのは、いうまで
もなく上の誤差が  という形で書けるという仮定が厳密には正しくない
からである。これは誤差の主要項であるに過ぎないので、この項を消せば次の
項が出てくる。具体的に次の項を考えてみると、
という形で書けるという仮定が厳密には正しくない
からである。これは誤差の主要項であるに過ぎないので、この項を消せば次の
項が出てくる。具体的に次の項を考えてみると、

と書けるとすれば、これから求めた「真の値」は

となって、結局 4 次にしかなっていないということがわかる。
なお、ここで 2 次の項の次が 3次ではなくて4次になるとしたが、これは台形 公式でも中点公式でもなりたつ特別な性質である。
さて、こうなると、次は  の項も消せないかという欲が出てくるであろ
う。実はそういうことも出来るわけで、そのためには
の項も消せないかという欲が出てくるであろ
う。実はそういうことも出来るわけで、そのためには 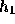 と
と 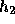 の2個
ではなく、さらにもう一つ別の刻み幅で積分してやればいい。そうすると、
の2個
ではなく、さらにもう一つ別の刻み幅で積分してやればいい。そうすると、

と近似して、 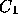 と
と 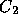 の両方を決めた上で S の高精度の推定値を
作ることが出来る。これは、結局 S(h)を
の両方を決めた上で S の高精度の推定値を
作ることが出来る。これは、結局 S(h)を 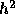 の関数として2次多項式近似
していることになる。
の関数として2次多項式近似
していることになる。
ここでやるのは、結局前回やった線形多段階法の場合と同様に、多項式補 間を作るということである。が、線形多段階法の場合とは違って、補間多項式 をもう一度積分するとかそういう必要はない。この時は、特別な計算法(ネヴィ ユのアルゴリズム)として知られる方法を使うことが出来る。
まず、一般的な場合についてネヴィユのアルゴリズムを示しておく。標本点
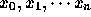 (ただし、 これらは降順または昇順にならんでいる
必要がある) での補間したい関数 f の値を
(ただし、 これらは降順または昇順にならんでいる
必要がある) での補間したい関数 f の値を 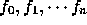 とす
る時、
とす
る時、 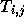 を以下のように定義する
を以下のように定義する

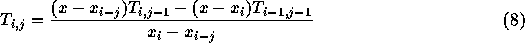
すると、一般に 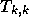 というのが、点
というのが、点 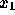 から
から 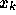 までを使った
k次補間多項式の x での値ということになる。特に、
までを使った
k次補間多項式の x での値ということになる。特に、 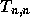 は全部
の点をつかった、もっとも精度が高いことが期待される近似値になる。
は全部
の点をつかった、もっとも精度が高いことが期待される近似値になる。
特に、 x= 0 のところでの値を求めるなら、上の式で x=0 とすればいい から、

という形になる。
結局、表に示すように、左と左上の値から次のを計算できることになる。
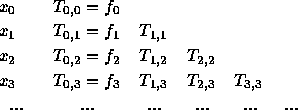
このやりかたで作った補間値が、 n 次まで正しいということは前回と同様 に証明できる。
この方法を使えば、任意の標本点数をつかっていくらでも高次の補間多項式を つくり、いくらでも高精度の近似値をえることができるということになる。こ のような、パラメータ h のいくつかの値で近似値を求め、その補間多項式 から h=0 での値を推測する方法のことを一般にリチャードソンの補外とい う。
なお、数値積分の話として考えると、積分 Sが

というように奇数次もあるような展開をもつならば、補間多項式は n 次に
しかならないが、台形公式のように偶数次しか持たない場合には 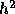 の多
項式として近似値を作ることができる。この時は次数が 2n次になることに
注意して欲しい。
の多
項式として近似値を作ることができる。この時は次数が 2n次になることに
注意して欲しい。
数値積分の場合にもっとも普通に使われるのは、台形公式とリチャードソン補 外の組合わせであり、これにはロンバーグ積分法という特別な名前がついてい る。ロンバーグ法の場合、h を半分にしていく。これは、台形公式では h を半分にした時に、元の h で計算した値はそのまま使えるので、計算量が 得になるからである。結局、普通の台形公式と同じ計算量ではるかに高い計算 精度が達成できることになる。
リチャードソン補外の考えを常微分方程式に適用しようというのがグラッグ法 である。以下のことに注意したい:
これらの問題のために、常微分方程式に対して補外法が使えるということが初 めて示されたのは 1965 年と比較的最近のことである。(線形多段階法やルン ゲ・クッタ法は前世紀から使われている)
陽的な公式で、誤差に奇数次の項がないものを構成できるかというと、これは 実は可能であるということが知られている。もっとも普通に使われるのは、陽 的中点公式と呼ばれる以下の公式である。

これは、前回述べた線形多段階法の一つである。これと、前進オイラー法によ る出発公式

を組み合わせたものは(ステップ数が偶数なら))、 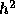 による漸近展開
をもつことが知られている。従って、この組合せを使うと、リチャードソン補
外によって超高精度の積分公式を作れる。これを通常グラッグ法と呼ぶ。
による漸近展開
をもつことが知られている。従って、この組合せを使うと、リチャードソン補
外によって超高精度の積分公式を作れる。これを通常グラッグ法と呼ぶ。
補外法はまだ比較的新しい方法であり、理論的に良くわかっていないことも多々 ある。ここでは、そのいくつかの問題点について簡単に触れる。
次週以降の話題の先取りになるが、陽的中点公式は安定ではないということが 知られている。ここで、安定ではないとは、安定な線形常微分方程式に適用し た時に、数値解が0にいかないということである。
このことが問題かどうかははっきりしていないが、理論的にはそういう問題を 押えるはずである方法というものが知られている。
これまで、補間にはいつでも多項式を使ってきたが、これはもちろんもとの関 数がよい性質(近くに特異点がないこと)を持っていることを必要とする。こ れに対し、有理関数補間をすれば、近くに特異点があってもうまくいく(かも しれない)。というわけで、有理関数で近似すればいいことがあるのではない かという話になる。
有理関数となると一意には決まらないが、通常は分子と分母が等しい次数にな るように作る。補外法にこれをつかったものを Bulirsch-Stoer 法と呼び、ラ イブラリなどではこれが実装されたものが多い。が、グラッグ法に比べて圧倒 的にいいかというと、そうでもないようである。
ここで時間刻みというと、 2 つの意味がある。つまり、初期値問題を解く時 に、通常は比較的小さな区間(これを Hとする)に全体を分けて、この H に対して補外法を使う。これは、Hを無制限に大きくとるといろいろ微妙な 問題が起きるからである。
この H を決めたとしても、さらに、そのなかで h (の列)をどうとるか という問題がある。
通常は、  のとり方を適当に決める(例えば、
のとり方を適当に決める(例えば、 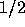 にしていく、ある
いは大体
にしていく、ある
いは大体 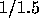 程度にしていく等)。で、誤差を見ながら H のほうを変
える。誤差推定には、例えば、最終的な補外の値と、一つ点が少ないものとの
差を使うのが実用的である。
程度にしていく等)。で、誤差を見ながら H のほうを変
える。誤差推定には、例えば、最終的な補外の値と、一つ点が少ないものとの
差を使うのが実用的である。