 から
から 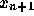 にいくのに前に計算
した情報とかなにかを使うわけではないので、刻み幅は任意にとることができ
る。問題は、どうやって刻み幅を決めるかである。
にいくのに前に計算
した情報とかなにかを使うわけではないので、刻み幅は任意にとることができ
る。問題は、どうやって刻み幅を決めるかである。
さて、高次の公式を使うにしても、実際に問題を解こうという上ではいろいろ 考えないといけないことがある。もっとも重要なことは、刻み幅 h をどう やって決めるかということである。
前にやった大域誤差解析では、ある範囲で導関数(高次の公式なら一般に高次 の導関数)が最大値を持てば、その最大値と刻み幅の関数で数値解の誤差が押 えられるという話をした。が、実際問題としては、解いていくにつれて導関数 の値が大きく変わるといったことは普通に起きる。このために、刻み幅が一定 のままで計算していくというのは非常に無駄なことが多い。
無駄を減らすためには、局所誤差が小さい(解が滑らかな)ところは刻みを大 きく、逆に解が急にかわるところでは刻みを小さくしてやればよい。このよう な方法を可変刻み (variable step) 、あるいは適応刻み (adaptive step) と いう。
例えば Runge-Kutta 法の場合、  から
から 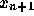 にいくのに前に計算
した情報とかなにかを使うわけではないので、刻み幅は任意にとることができ
る。問題は、どうやって刻み幅を決めるかである。
にいくのに前に計算
した情報とかなにかを使うわけではないので、刻み幅は任意にとることができ
る。問題は、どうやって刻み幅を決めるかである。
これにはいろいろな考え方があるが、通常使われるのは、局所離散化誤差を推 定して、それがある値以下になるようにするという方法である。
このための一つの考え方は、以下のようなものである。
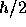 ずつ 2回に分けて積分する。
ずつ 2回に分けて積分する。
誤差の推定値が求まったら、普通は次のステップを調節する。局所離散化誤差 の次数がわかっているから、それに応じてステップサイズを調整すればよい。 次数プログラムによっては、現在のステップでの誤差が予定した値よりも大き ければステップを小さくして計算し直すようになっているものもある。
実装(プログラムを作ること)が容易であることもあって、この方法はわり と広く使われている。が、かなり無駄が多い方法であるというのも確かである。 というのは、単に誤差の推定のためだけに、 50% の無駄な計算をしているか らである。
もうちょっとうまい方法はないかということで、以下のようなことを考えた人 がいる。
一般に、 RK型の公式では、最終的な値は

の形になっている。ここで、 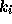 は全部そのまま使って、
は全部そのまま使って、 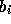 を別の
を別の
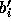 に置き換えた
に置き換えた

で、局所離散化誤差が元の公式よりも大きいが、むやみと大きくはない(例え ば、一次次数が低い)ものがあれば、元の公式との差を誤差の推定に使うこと ができる。
この形の公式のことを埋め込み型 embedded 公式という。最初に提案した人の 名前をとって Runge-Kutta-Fehlberg 公式ということも多い。これもいろいろ 提案されているが、上の Dormand-Prince 公式はすべて埋め込み型であり、こ れが最近はもっとも広く使われている。精度が高いものが必要な時は、 8次の公式が使われる。これらは
http://www.unige.ch/math/folks/hairer/software.htmlから入手できる (Fotran と C がある)。