さて、初期値問題である。直観的には、初期値問題であれば、初期値があれば その少し後の値が決まり、その少しあとの値が決まればまたそのあとも、、、 ということで決まっていく（数値解---計算機で求める解---は実際にそんなふ うにする）わけで、そういう方針で構成的な解の存在証明をすることも不可能 ではない。が、普通の教科書（常微分方程式論の）にのっているのはピカール の方法というものなので、一応それにそって説明する。
常微分方程式の初期値問題
の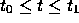 
での解を考える。今、 関数f が領域
で連続であり、最大値、最小値をもつと
しよう。絶対値が M でおさえられ、 
という関係がなりた
つとする。さらに、上の範囲の任意の t, xと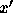 
についてリプシッツ条件
を満たすものとする。
このとき、上の常微分方程式の初期値問題の解は存在し、しかもただひとつで あるというのが。解の存在と一意性についてのコーシー・リプシッツの定理で ある。
以下、証明である。証明のためには、逐次近似といわれる方法を使う。具体的 には以下の関数列を考える。
まず、この関数列が以下の性質をもつということを示す。
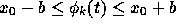を満たす
これらは帰納法で示せる。面倒なので省略。次に、この関数列が一様収束する ことを示そう。このためには、級数
（これは定義により 
と同じもの）の一様収束が示せればよい。
である。ここでリプシッツ条件から
となる。今、 k=1の場合について考えると、
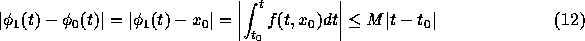
したがって、
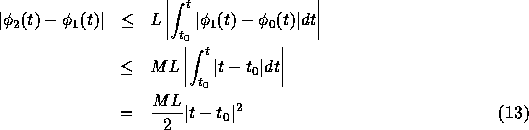
あとは同様にして
がいえる。従って、右辺の和が一様収束すれば左辺も一様収束する。ところが、 右辺の和は指数関数のテイラー展開になっているので一様収束する。つまり、 極限が存在する。
この級数の極限は、結局もとの方程式の解になっている。 なお、一意性についての証明は面倒なので省略する。
さて、ここまででは、リプシッツ条件を満たす狭い範囲でしか解が出来ていな いが、一般にはその先に延ばしていくことが出来る。これを解の延長という。
ここで求まって（というか、あることが示された）解は、可積分でなくても存 在するということをもう一度注意しておく。前に示した3体問題の解は、そう いう意味で存在しているわけである。
