陰的ルンゲ・クッタとガウス・ルジャンドル多項式による数値積分の関係にみ るように、数値積分と常微分方程式の数値解法には密接な関係がある。理論的 には、これは結局リプシッツ条件のもとで、常微分方程式の数値解は数値積分 で近似できるということから来る。
線形多段階法も、多項式近似した上で数値積分する方法というふうに理解でき る。このような方法で非常に高い次数を達成しようとすると、計算量、メモリ の必要量がどんどん増えてしまって現実的ではなくなる。また、あとで述べる ように安定性や収束性の問題もおきてきて、非常に高次の方法というのはかな らずしも実用的ではない。
では、もう少しうまい方法はないかというのが問題である。
例えば、数値積分において、簡単な台形公式を使った場合を考えてみる。これ で刻み幅をいろいろ変えれば、誤差は大雑把にいって刻み幅 h の2乗に比例 するはずである。
つまり、例えばある刻み幅 
と、別の刻み幅 
で計算した答の誤差は、
それぞれ、ある（共通の）定数 C を使って
と書けるような気がする。これをさらに言い換えると、積分の近似値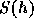 
が、真の値 S を使って
さて、この式から、「Sを求める」ことが出来る。つまり、
としてやると、「真の値」が求まってしまう。
図にするとこんな感じかな：
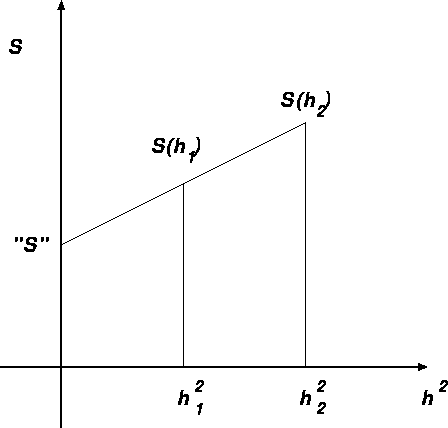
要するに、 
に対して誤差が一次式で書けると信じて、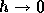 
での積分の値を求めてやるわけである。
もちろん、これで本当の真の値が求まるわけではない。というのは、いうまで
もなく上の誤差が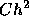 
という形で書けるという仮定が厳密には正しくない
からである。これは誤差の主要項であるに過ぎないので、この項を消せば次の
項が出てくる。具体的に次の項を考えてみると、
と書けるとすれば、これから求めた「真の値」は
となって、結局 4 次にしかなっていないということがわかる。
なお、ここで 2 次の項の次が 3次ではなくて4次になるとしたが、これは台形 公式でも中点公式でもなりたつ特別な性質である。
さて、こうなると、次は 
の項も消せないかという欲が出てくるであろ
う。実はそういうことも出来るわけで、そのためには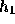 
と 
の2個
ではなく、さらにもう一つ別の刻み幅で積分してやればいい。そうすると、
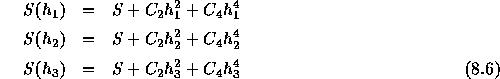
と近似して、 
と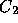 
の両方を決めた上で S の高精度の推定値を
作ることが出来る。これは、結局 S(h)を 
の関数として2次多項式近似
していることになる。