
ガウス型公式について述べる前に、まずそれと非常に関係の深い数値積分公式 について説明しておく。
数値積分とは、一変数であれば

と、微分方程式ではなく単に関数として与えられたものに対して、ある固定区
間 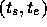 での定積分を数値的に求めることである。一般に、解析的に
積分ができないようなものを計算しないといけないことはよくあるので、そう
いうものが必要になることは多い。
での定積分を数値的に求めることである。一般に、解析的に
積分ができないようなものを計算しないといけないことはよくあるので、そう
いうものが必要になることは多い。
数値積分法として、すでに皆さんが知っているであろうものは、たとえば
例えば台形公式は、等間隔に区間を分けたとして、ある部分区間での積分を

と、両端を結んだ台形の面積で近似するということに相当する。これに対して、 もっとましな方法というのを理論的に考えられないであろうか?
一つの方法は、区間の中の点をいくつかとって、それらを通る補間多項式を作 り、それを積分することである。中の点を等間隔にとったものをニュートン・ コーツ型の公式という。
さて、一般に補間するための点をp個とった時、 p-1次の多項式を持って くればそのすべての点を通るように出来る。ニュートン・コーツ型の公式はそ のような最小次数多項式を使うものである。例えばもとの関数が実際にp-1 次以下の多項式ならば、厳密に正しいものが求まる。
この補間の原理を説明しておく。例えば補間に使う点が 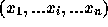 とあ
るとすれば、以下のような多項式を考える
とあ
るとすれば、以下のような多項式を考える
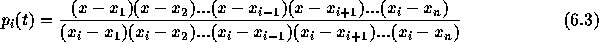
この多項式は、 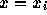 で 1、それ以外のすべての
で 1、それ以外のすべての 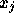 で0になる。従って、
補間多項式は
で0になる。従って、
補間多項式は

とすればいい。
数値積分に使うには、あらかじめ 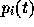 の積分を求めておいて、それと
の積分を求めておいて、それと
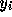 を掛けて和をとるだけである。
等間隔でなく点をとることで精度をあげることはできないかというのが、ここ
での問題である。
を掛けて和をとるだけである。
等間隔でなく点をとることで精度をあげることはできないかというのが、ここ
での問題である。
ここで、一般的に、不等間隔に点をとってなんとかするという観点から考える こともできるが、なかなか難しいので答のほうから考えていく。
答は、「ガウス・ルジャンドルの多項式の零点を点にとると、次数を最大にで
きる」というものである。ガウス・ルジャンドルの多項式は、有限区間で帰納
的に定義できる直交関数系である。つまり、最初の項を定数として、k番目
の項は k次多項式であって、それまでの項すべてと直交するようにとるので
ある。つまり、関数基底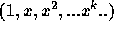 にグラム・シュミットの直
交化を適用したものがガウス・ルジャンドルの多項式である。
にグラム・シュミットの直
交化を適用したものがガウス・ルジャンドルの多項式である。