ここは前回の残りである。 前回は、ジーンズ不安定の不安定領域の振る舞いは流体と恒星系で定性的には 同じだが、安定領域では流体は音波モードになるのに対して恒星系では普通の 波はなく、完備なモードは van Kampen モードという超関数で書くようなもの だという話をした。
さて、モードがあって、世の中はその重ね合わせであるというのなら、それで
話はおしまいではないかとおもうのが人情だが、普通はそういう話にはなって
いない。というのは、 Landau Damping という難しいものがあるということに
なっているからである。これはどういう原理ででてくるかというと、要するに
複素数の ![]() があると信じて、そういう解を求めると、ちゃんとそうい
うものが見つかるというものである。つまり、摂動の速度方向の分布
があると信じて、そういう解を求めると、ちゃんとそうい
うものが見つかるというものである。つまり、摂動の速度方向の分布 ![]() を
うまくとってやると指数関数的に減衰するモードがでてくる。ただし、注意し
て欲しいのは、これは、
を
うまくとってやると指数関数的に減衰するモードがでてくる。ただし、注意し
て欲しいのは、これは、 ![]() に制限をつけないと出てこないということであ
る。不連続な
に制限をつけないと出てこないということであ
る。不連続な ![]() を仮定すれば、時間のベキでしか減衰しないような解を構
成することも出来る。ただし、そういった解はモードの形、つまり位置、時刻
の指数関数の形に単純に書けるとは限らない。
を仮定すれば、時間のベキでしか減衰しないような解を構
成することも出来る。ただし、そういった解はモードの形、つまり位置、時刻
の指数関数の形に単純に書けるとは限らない。
逆にいえば、解が指数関数の形に書けると仮定すれば、ジーンズ波長より短け ればそれは指数関数的に減衰するわけである。
今、簡単のために重力がない一次元系を考える。この時 van Kampen mode は
単なる ![]() 関数なので、初期の波数が
関数なので、初期の波数が ![]() であるような摂動は
であるような摂動は
| (1) |
しかし、注意して欲しいのは、これは最初に安定性解析の時に仮定した
![]() という形とは違うということである。これは、
振動数
という形とは違うということである。これは、
振動数 ![]() が
が ![]() そのものであり、速度空間のなかでの位置に依存する
ためである。
そのものであり、速度空間のなかでの位置に依存する
ためである。
このことをいいかえると、上のような「自然な」解があるにもかかわらず、 モード解析をするとvan Kampen mode のような singular なものが出てくるの は、モード解析の仮定として位相速度が粒子の速度に寄らないようなものを考 えたからであるともいえる。
さて、上の「自然な」解はどのように振舞うかをちょっと見てみよう。
密度は、
 |
(2) |
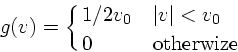 |
(3) |
このような減衰が起きるのは、初期条件が非常に特別なものであるためである ということに注意してほしい。つまり、速度ごとに波の位相速度が違うのに、 初期条件としてその空間位相がすべてそろったものを考えたわけである。そう すると、時間がたてば位相はずれていくので速度方向に積分して見た波の振幅 は小さくなってくことになる。これは、速度方向の「波数」に時間が生で入っ てくるためである。
なお、 ![]() に適当な形を仮定すれば、もっと速く減衰するものも作れる。
に適当な形を仮定すれば、もっと速く減衰するものも作れる。
もちろん、無衝突ボルツマン方程式にしたがった進化は可逆過程である(エン トロピーを生成しない)ので、原理的には逆に振幅が大きくなるような初期条 件も存在していないといけない。実際、減衰していく解で、どこかで時間反転 すればそういう解が作れるわけである。
なお、今日の話で要領を得ないと思った人は、、、この辺は基本的で大事な問 題であるわりにはあまり良いテキストも論文もないので、なかなか難しい。