


Next: 4 Jeans 不安定
Up: 理論天体物理学特論I
Previous: 2 恒星系でのジーンズ不安定とランダウ減衰
何度も出てきたがもう一回式を書いておく。
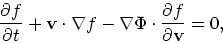 |
(15) |
ここで 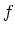 は6次元位相空間での分布関数である。
は6次元位相空間での分布関数である。 は重力ポテンシャ
ルであり、以下のポアソン方程式の解として与えられる。
は重力ポテンシャ
ルであり、以下のポアソン方程式の解として与えられる。
 |
(16) |
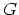 は重力定数であり、
は重力定数であり、  は空間での質量密度
は空間での質量密度
 |
(17) |
である。
これを流体の時と同様に線形化して、その振舞いを調べる。分布関数を 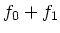 、ポテンシャルを
、ポテンシャルを
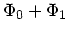 とし、添字0がつくほうは定常解で
あるとして式を整理すれば
とし、添字0がつくほうは定常解で
あるとして式を整理すれば
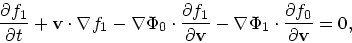 |
(18) |
 |
(19) |
ということになる。これが線形化された無衝突ボルツマン方程式である。
Jun Makino
2003/11/16