


Next: 4 ビリアル定理の応用
Up: 理論天体物理学特論I
Previous: 2 Jeans Equations
前節では、Collisionless Boltzman 方程式の速度空間でのモーメントを考え
て Jeans 方程式を導いた。ここではさらに空間全体のモーメントをとる。
式6において、密度 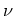 を質量密度
を質量密度 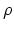 で置
き換え、さらに
で置
き換え、さらに  を掛けて空間全体で積分する。
を掛けて空間全体で積分する。
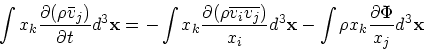 |
(13) |
右辺の最初の項は、例によって発散定理を使って書き直せる。
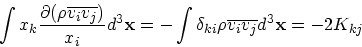 |
(14) |
これは、運動エネルギテンソル 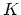 の定義を与える。ついでに第
二項はポテンシャルエネルギーテンソル
の定義を与える。ついでに第
二項はポテンシャルエネルギーテンソル 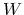 と呼ばれるものであ
る。
と呼ばれるものであ
る。
さらに、
 の定義を使って、
の定義を使って、
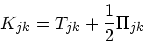 |
(15) |
但し
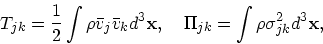 |
(16) |
さらに、 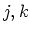 についての式と
についての式と  についての式を足してやると
についての式を足してやると
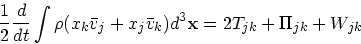 |
(17) |
さらに、慣性モーメントテンソル
 |
(18) |
を導入して、連続の式とか発散定理とかを使うと
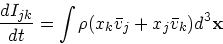 |
(19) |
で、結局
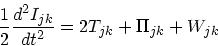 |
(20) |
これをテンサービリアル定理という。
さて、今定常状態 ( の時間微分が0)を考え、さらに上の式のトレースを
とってみると、
の時間微分が0)を考え、さらに上の式のトレースを
とってみると、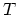 ,
, 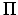 の定義からこれらの寄与は全運動エネルギー
の定義からこれらの寄与は全運動エネルギー の
2倍になる。
の
2倍になる。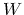 の方は、
の方は、 の定義を使えば
の定義を使えば
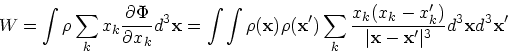 |
(21) |
ここで 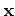 と
と 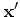 を入れ換えた積分を書き、両方を足すと
を入れ換えた積分を書き、両方を足すと
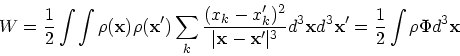 |
(22) |
というわけで、 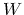 は系の全ポテンシャルエネルギーである。結局、
は系の全ポテンシャルエネルギーである。結局、
 |
(23) |
が成り立つ。これを、スカラービリアル定理、または単にビリアル定理という。
今、系の全エネルギーを Eとすれば、 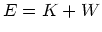 であるから、
であるから、
 |
(24) |
ということになる。つまり、定常状態にある自己重力恒星系では、必ず全エネルギーは
ポテンシャルエネルギーのちょうど半分であり、絶対値が運動エネルギーに等
しい。これは球対称とかそういう仮定なしに常に正しい。



Next: 4 ビリアル定理の応用
Up: 理論天体物理学特論I
Previous: 2 Jeans Equations
Jun Makino
2003/11/9
![]() を質量密度
を質量密度 ![]() で置
き換え、さらに
で置
き換え、さらに ![]() を掛けて空間全体で積分する。
を掛けて空間全体で積分する。
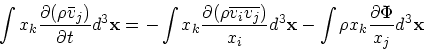
![]() の定義を使って、
の定義を使って、
![]() の時間微分が0)を考え、さらに上の式のトレースを
とってみると、
の時間微分が0)を考え、さらに上の式のトレースを
とってみると、![]() ,
, ![]() の定義からこれらの寄与は全運動エネルギー
の定義からこれらの寄与は全運動エネルギー![]() の
2倍になる。
の
2倍になる。![]() の方は、
の方は、![]() の定義を使えば
の定義を使えば
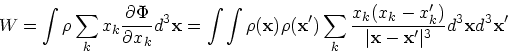
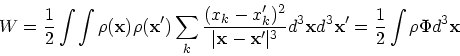
![]() であるから、
であるから、