 に対応し、少しでもエネルギーが増えるような移動はしな
いということに対応する。したがって、計算を始めたところの近くに局所的な
極小値があれば、そこに落ち込んで計算が止まってしまうからである。
に対応し、少しでもエネルギーが増えるような移動はしな
いということに対応する。したがって、計算を始めたところの近くに局所的な
極小値があれば、そこに落ち込んで計算が止まってしまうからである。
さて、メトロポリス法はいいとして、それが最適化とどう関係するかという話 に戻る。メトロポリス法では、とにかくある温度でのアンサンブル平均を実行 できた。しかし、最適化によって我々がやりたいのは、ある関数の最小化であっ て別に平均でもなんでもない。
ここで、温度 ![]() の極限を考えると、熱力学的にはもちろん温度
の極限を考えると、熱力学的にはもちろん温度 ![]() の極限
はポテンシャルエネルギーの極小値に対応する。が、温度
の極限
はポテンシャルエネルギーの極小値に対応する。が、温度 ![]() で機械的にメ
トロポリス法をやってもうまくいくとは限らない。というのは、温度
で機械的にメ
トロポリス法をやってもうまくいくとは限らない。というのは、温度 ![]() は
は
 に対応し、少しでもエネルギーが増えるような移動はしな
いということに対応する。したがって、計算を始めたところの近くに局所的な
極小値があれば、そこに落ち込んで計算が止まってしまうからである。
に対応し、少しでもエネルギーが増えるような移動はしな
いということに対応する。したがって、計算を始めたところの近くに局所的な
極小値があれば、そこに落ち込んで計算が止まってしまうからである。
局所的な極小値に落ち込まないようにするには、最初は高い温度にしておいて、 ある程度位相空間全体を動けるようにしてメトロポリス法を適用し、それから 温度を下げてはまたメトロポリス法で動かすというのを繰り返すという方法が 考えられる。これが SA 法である。
実際上は、
といったことを考えないといけない。この辺は理論がないわけではないが、そ
れは例えば収束性を保証するためには温度は
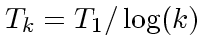 というふ
うに繰り返し数
というふ
うに繰り返し数 ![]() の対数でしか温度を下げられないというようなものなの
であまり役に立たない。実際には、
の対数でしか温度を下げられないというようなものなの
であまり役に立たない。実際には、 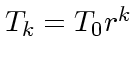 という風に指数関数的
に温度を下げても意外にうまくいってしまう。そういうわけで、実際に問題を
持ってきた時に上のようなパラメータ(総称してアニーリング・スケジュール
ということが多い)をどう決めるかは、いろいろ実験してみる必要がある。
という風に指数関数的
に温度を下げても意外にうまくいってしまう。そういうわけで、実際に問題を
持ってきた時に上のようなパラメータ(総称してアニーリング・スケジュール
ということが多い)をどう決めるかは、いろいろ実験してみる必要がある。