6 練習

1. 一次元調和振動子

   
   

   $$\frac{d^2 x}{dt^2} = -kx$$ (18)

   
   

   について、初期条件
   

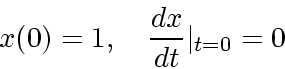   $$x(0) = 1, \quad \frac{dx}{dt}\vert _{t=0} = 0$$ (19)

   
   
   からの、 $t=2\pi$ までの数値解を、古典的ルンゲ・クッタ公式を使って求め よ。刻み幅をいろいろ変えて、精度が刻みにどのように依存するか、また、ど こまで高い精度が実現可能か調べ、なぜそうなるかを考察せよ。

   なお、牧野が書いたプログラムが

   http://grape.astron.s.u-tokyo.ac.jp/~makino/pcphysics/programs/index.html
   

   の hermonic5a.C にあるので、今回はこれをコピーしてコンパイル・実行する だけでも一応いいことにする。但し、これは古い C++ の規格にそって書かれ ているので色々変更が必要である。

2. 刻み幅が等しい場合について、以下の公式を導け
   • 4次の陽的アダムス公式
   • 4次の陰的アダムス公式
   • 4次の陽的シュテルマー公式

   但し、シュテルマー公式とは、2階の微分方程式用の公式である。時間の2階微 分に、偏微分方程式の時に使ったのと同じ3点を使う中心差分を使う。

3. 上で導いた4次の陽的・陰的アダムス公式を使って、1と同じ単振動の方 程式について同様な解析を行なえ。出発公式にはルンゲ・クッタを使うか、あ るいは厳密解をつかってもよい。

4. 陰的線形多段階法について、直接代入法が収束する速さが何で決まるか を考察せよ。