1 放物型方程式

物理・天文で出てくる偏微分方程式は大抵は 2 階である。で、普通は空間3次 元と時間1次元の4次元空間で定義されるわけだが、この講義ではいくつかの特 殊な場合を除いて空間1次元時間1次元の2次元で考える。 これは、そうしておかないとプログラムを書くのも、また計算機のほうも大変 になるからである。

放物型方程式ってのは何か？というのは皆さん知っているはずなので（だよね？） 厳密な定義は省くが、要するに以下の形に書ける（移流）拡散方程式のことで ある。

$$\frac{\partial u}{\partial t} = -K \frac{\partial u}{\partial x} + D \frac{\partial^2 u}{\partial x^2}$$ (1)

ここで $x$, $t$ はそれぞれ空間、時間を表す変数であり、 $u$ は方程式が 記述する量である。拡散方程式として見ればなにかの濃度ということになるし、 熱伝導の方程式としてみれば温度なりエンタルピーなりということになる。 $K$ は一次の係数で、これは普通の拡散方程式や熱伝導方程式では 0 である。 これが 0 でないのはどういう場合かというのは後でちょっと考える。 $D$ が 普通の拡散係数ということになる。今は $D$ が空間・時間に依存しない場合 を考える。

依存しない場合はもちろん変数分離で解けるので、数値計算することに意味が あるのは$D$ が空間・時間に依存する場合だが、まあ、とりあえずは答がわか る場合を計算してみることにしよう。

放物型方程式の場合には、初期条件と境界条件を与えないと解が定まらない。 以下では、

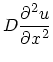$$\frac{\partial u}{\partial t} = D\frac{\partial^2 u}{\partial x^2}$$ (2)

$$0<x<1,\quad 0<t,\quad u(0,t) = u(1,t)=0,\quad u(x,0)=u_0(x)$$

という固定境界の場合を考える。