| (22) |
の数値解を、
![]() の時に適当な陰的公式と陽的公式
(後退オイラーと前進オイラーでもOK)で求めてみよ。
の時に適当な陰的公式と陽的公式
(後退オイラーと前進オイラーでもOK)で求めてみよ。
- ルジャンドル多項式の 0 点をとるということから公式を導け。
- 実際に線形系に適用して、4次精度であることと A-安定であることを確かめよ。
- 2変数以上の場合に適用出来るプログラムを作り、適当な非線形方程式
を解いてみよ。例えば van der Pol 方程式
で極度に非線形性の強い場合につ いて、4次の古典的ルンゲクッタと解の精度、信頼性等を比較してみよ。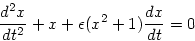
(23)