2 ルンゲ・クッタ（復習）

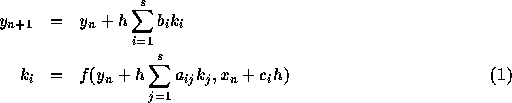
計算天文学 I では、ルンゲ・クッタ(RK) 法とそのバリエーションを扱った。 ルンゲクッタ法とは、非常に一般的には以下のような形に書ける方法である。

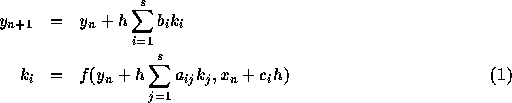
自然数 s を段数（number of stages）という。 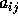, , 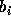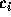はパラメータであるが、a と c は普通

となるようにとる。これは、一般にそうでないような公式は不可能ではないが あまりいいことがない（精度がよくならない）からである。

と、こう、式に書いてしまうとすぐにはわからないが、例えば s=2の場合に 書き下してみると

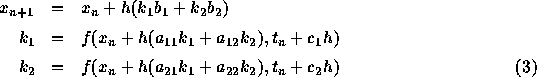
と、まあ、こんな感じになる。こちらを良く見ればすぐにわかるように、

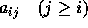1. がすべて0ならば、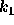から順に計算していくこと ができる。つまり、「陽的」公式になっている。

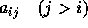2. が0のときは、各 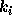についての式に 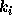だ けが入ってくる。これを半陰的 (semi-implicit) 公式という。この場合には、 まず 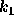についての方程式をといて、次に 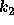についてのを解いて、、、 と順番に計算出来る。

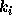3. 上のような制約が全くない時は、「陰的」公式ということになる。この ときは、すべての に対する（一般には非線形な）方程式を一度に解く 必要がある。

今日はとりあえず陽的な公式だけを考える。 形式的には、もっとも簡単な前進オイラー法もルンゲ・クッタ公式の一つとい うことになるが、まあ、普通もっとも簡単なRK法というと、2次の公式

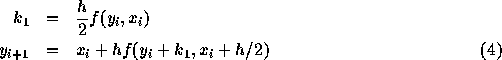
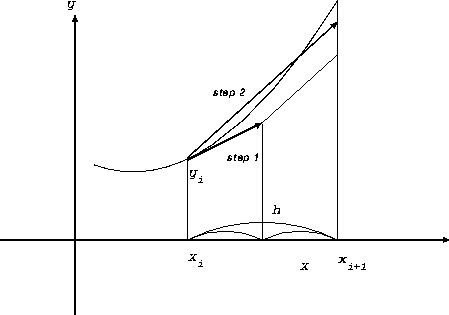
である。 この方法がどのように働くかについては、図的な説明というものが可能である。元の点からまずオイラー 法と同様に接線を引く。が、これを次の時刻まで延ばすのではなく、ステップ の半分のところで止める。で、ここでもう一回微分方程式の右辺を評価する。 ここでの導関数の値を使って、もとのところ 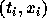から直線を引くわ けである。

普通は、RK法というといわゆる古典的 RK 公式

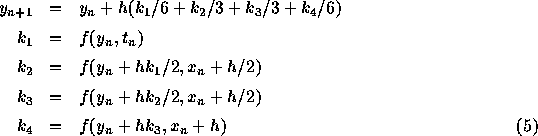
のことをさす。これは、いろいろ良い性質をもつ。例えば

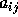1. が i-j=1 以外すべて0なので、右辺の計算が楽である。
2. 次数が4次であり、4段陽的公式で到達可能な最高次数を達成している
3. 係数が簡単な有理数なので、プログラムしやすい。また丸め誤差を小さ くできる。

4次よりも高精度な公式というのも非常によく研究されていて無数にいろんな ものが知られている。ただし、4次よりも高い次数では、次数よりも必要な段 数が大きくなる。この2つの関係が一般にどうなるかは未解決の問題である。 というようなこともあるので、よほど変わったことをしたいというのでない限り、専門 家が作った公式を使うのが無難である。

Dormand と Prince は、最近、段数／次数のさまざまな組合せについて、 離散化誤差を非常に小さくした公式を求めた。これらは、

http://www.unige.ch/math/folks/hairer/software.html

普通の（というのがどういう意味かは今のところ明らかではないが）常微分方 程式を手軽に解くにはこれらのRK公式を使えば十分である。

実用的には、こちらが欲しい計算精度をどうやって達成するかという問題があ る。この問題を解決するためには、誤差を推定しながら積分の刻み幅を自動的 に調節する必要がある。これについては次回にちょっと触れる。