6 レポート課題

1は必須。後はオプション。 プログラムが必要なものはプログラムを提出 すること。

1. TSP について、 参考プログラム

   http://grape.astron.s.u-tokyo.ac.jp/~makino/
           kougi/keisan_tenmongakuII/programs/index.html
   

   にある anneal.C を動かしてみて、単位正方形内にランダムに 100 個 程度の点をばらまいた時にどんな答がでるか見てみよ。また、アニーリングス ケジュールをいろいろ変えてみて、答がどのように変わるか調べよ。

2. 規則的に点を並べた場合には、TSP の厳密解が全数探索をしなくても求まる。 100点程度の場合にそのような厳密解がある場合を作ってみて、 SA で厳密解 に到達できるかどうか調べよ。

3. 参考プログラムではコストがユークリッド距離であるとしている。これ をマンハッタン距離(|x|+|y|)にして、答の変化を見てみよ

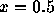4. のところに川があって、川を渡るのには 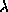のコストが余計に掛かるとして答の変化を見てみよ。もっともらしいか？また、 どのようにしてもっともらしいと判断したか？

5. 「単位正方形の中に n 個の円を重ならないように詰め込めるような 円の最大半径はいくつか」という問題を、「円の詰め込み問題」という。いく つかの n については厳密解が知られているが、一般の n について解かれ ているわけではない。これを SA で解いてみて、どれくらいもっともらしい答 がでるか調べよ。目的関数として、n 個の点間の距離と壁への距 離の最小値をとればよい。知られている厳密解のいくつかは以下にまとめられ ているので、比べてみること。

   http://www.cg.inf.ethz.ch/~peikert/personal/CirclePackings/