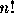 個の組合せを調べあげないと答がわからないようなもので
ある。この他にも、ナップザック問題とか最大充足問題とかいろんなものがあ
るが、 SA を使うという観点からすればどれも同じようなものである。
個の組合せを調べあげないと答がわからないようなもので
ある。この他にも、ナップザック問題とか最大充足問題とかいろんなものがあ
るが、 SA を使うという観点からすればどれも同じようなものである。
さて、もともとのメトロポリス法では、原理として考えていたのは多粒子系の 熱平衡とかそういうもので、あんまり組合わせ論的最適化という感じはしない。
組合わせ論的最適化というと、代表的なのは前回にあげた巡回セールスマン問
題(TSP)のような、 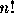 個の組合せを調べあげないと答がわからないようなもので
ある。この他にも、ナップザック問題とか最大充足問題とかいろんなものがあ
るが、 SA を使うという観点からすればどれも同じようなものである。
個の組合せを調べあげないと答がわからないようなもので
ある。この他にも、ナップザック問題とか最大充足問題とかいろんなものがあ
るが、 SA を使うという観点からすればどれも同じようなものである。
つまり、 SA という観点からすれば、
の2つを与えることができれば、あとはアニーリング・スケジュールを決めれ ば答がでる。さらに、前に述べた議論から、近くの解を発生する方法は、対称 性さえ満たしていれば適当でいい。収束の速さとかを考えると適当にするより いろいろ考えた方がいいのは当然だが、それは収束の速さに影響するだけだし その影響もあまり大きくないのが SA のいいところである。これは、条件が悪 いと実際上収束しなくなる最急降下法なんかとはだいぶ違う。
TSP は、以下のようにかける。
n個の点 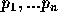 に対して、点間の移動コスト
に対して、点間の移動コスト 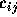 が与えら
れているとする。 n 個の点をすべて通ってもとに戻るような巡回路でコス
トの合計が最小になるようなものを見い出せ。
が与えら
れているとする。 n 個の点をすべて通ってもとに戻るような巡回路でコス
トの合計が最小になるようなものを見い出せ。
巡回路自体は、 n 個の点(の番号)の並び  で与えられる。
この並びは 1 から n までを並べ変えたもの、つまり、ここで
で与えられる。
この並びは 1 から n までを並べ変えたもの、つまり、ここで 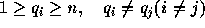 ということになる。
ということになる。
目的関数は、

(但し、 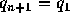 とする)であるので簡単に計算できる。近くの解
の発生のさせ方だが、もっとも簡単なのは
とする)であるので簡単に計算できる。近くの解
の発生のさせ方だが、もっとも簡単なのは 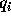 と
と 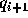 を入れ換えて
みるというものである。もっと大きくつなぎ変えたければ、適当に2箇所を選
んでそこで切ってひっくり返してつなぐというのも考えられる。こちらのほう
が、局所的な最適解に落ちる可能性が少ないという意味では安全である。
を入れ換えて
みるというものである。もっと大きくつなぎ変えたければ、適当に2箇所を選
んでそこで切ってひっくり返してつなぐというのも考えられる。こちらのほう
が、局所的な最適解に落ちる可能性が少ないという意味では安全である。
定義域が連続的な関数とは違って、動かす量を調整することで採用確率を調整 するのは難しいというか、組合わせ論的最適化の場合にはそういうのを考えて もしょうがない。
実際にプログラムを作る時には、定義式にしたがって目的関数を計算するので
はなく、つなぎ変えたことによる変化だけを計算すればいい。これによって一
回のモンテカルロ反復に対する計算量を 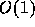 にすることができる。
にすることができる。
例えば、温度の変え方を指数型で 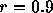 とし、一温度での反復は 100n
とか、採用されたのが 10n とか適当に決めて、大抵の場合にちゃんとした
答がでるようである。
とし、一温度での反復は 100n
とか、採用されたのが 10n とか適当に決めて、大抵の場合にちゃんとした
答がでるようである。
原理的には、近似解候補を与えた時に目的関数を計算する関数(手続き)と、
今の近似解からランダムに新しい近似解を作る手続きの2つがあればプログラ
ムは作れる。が、多くの場合に、「新しい近似解と今の近似解との差」を計算
するほうが計算量が減る。 TSP の場合であれば、これは 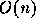 と
と 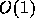 で非常に大きい。また、古典粒子系のモンテカルロのように目的関数が全粒子間のポテン
シャルエネルギーの和であれば、全部計算すれば
で非常に大きい。また、古典粒子系のモンテカルロのように目的関数が全粒子間のポテン
シャルエネルギーの和であれば、全部計算すれば 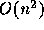 だが動かしたこと
による変化は
だが動かしたこと
による変化は 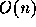 である。このように、変化分を高速に計算する方法を工
夫することが極めて重要になる。
である。このように、変化分を高速に計算する方法を工
夫することが極めて重要になる。
SA は、まあとにかく答がでるのが利点とはいえ、「ゆっくり冷やさないとい けない」という条件がつくので計算量は多い。また、メトロポリス法では配置 を作っては乱数と比べるというのの繰り返しなので、普通にやったんでは並列 化して沢山計算機を使って速くするのも難しい。
最近、さまざまな並列化手法が提案されている。特に注目されているのは温度 並列 SA (TPSA) というもので、計算機毎に違う温度でモンテカルロをやり、 時々違う温度のもの同士を交換するという方法である。温度がもっとも低いも ののところに最終的な結果が求まる。これは「レプリカ交換法」とかいろんな 名前がついているが、基本的な発想はみんな同じである。