RK 法は、「一段階」法である。これはどういう意味かというと、微分方程式
の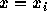 
での近似解 
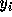があったとして、次の xの値 
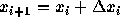での近似解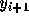 
を求めるのに、
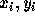と
微分方程式そのものだけで十分であるということである。中間のややこしい値
を計算する必要はあるが、それは RK 法のほうが勝手にやることで、使う方が
入力を与える必要はない。
これに対して、一段階ではない方法、つまり多段階法というのは、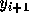 
を計算するのに、 
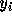以外の情報、例えば 
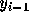や、そこで計算した
導関数の値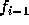 
、さらにもっと昔の情報を使うやりかたのことである。
これは、プログラムとしてはもちろんRK法に比べれば面倒になる。昔の値をとっ
ておかないといけないし、また、一番最初に計算を始める時にどうするかとい
う問題もあるからである。
さらに、「一段階でない」というだけなので、可能な計算法にあまりに多様な 可能性がある。例えば、以下のような方法が考えられる。
これは、陽的中点公式といわれるもので、式としては偏微分方程式の解法の時 に空間微分の1次の項に使った中心差分と同じ形になっている。従って、理屈 としては2次の精度をもった公式になっている。
この方法は、しかし、立派な名前までついているのにもかかわらず、実は使え ない公式である。
どのような問題があるのかを示すために、以下の線形方程式
に陽的中点公式を適用したらなにが起きるかを考えてみる。刻みは固定の
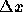とすると、離散化したものは
になる。これは線形差分方程式なので、前にもやったように固有値を調べれば
いい。今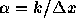 
として整理すると、固有方程式は
となって、これは実解を2つ持つ。それらを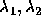 
とすれ
ば、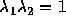 
なので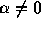 
ならどちらかは必
ず絶対値が 1 より大きい。
ちょっと式を見ればわかるように、絶対値が 1 より大きい固有値は
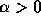、つまり k>0 なら負である。したがって、必ず振動的に発散す
ることになる。
なお、上のような、安定な線形微分方程式について振舞いを調べるというのが、 常微分方程式の安定性解析の基本になる。非線形な方程式では違うとかいろん なことがあるかもしれないわけだが、まあ、少なくとも線形安定でないと話に ならないし、それ以上のことは一般論としていうのは難しいからである。
さて、中点公式はともかくとして、使える線形多段階法はじゃあどんなものか というわけだが、これも無限にいろんな作り方がある。そのへんの詳しい話は そういう本に譲ることにして、ここではもっとも広く使われているアダムス法 について説明する。
原理は、いくつかのステップでの導関数（微分方程 式の右辺） fの値を憶えておいて、それを通る補間多項式を作り、それを積 分して解を求めようというものである。
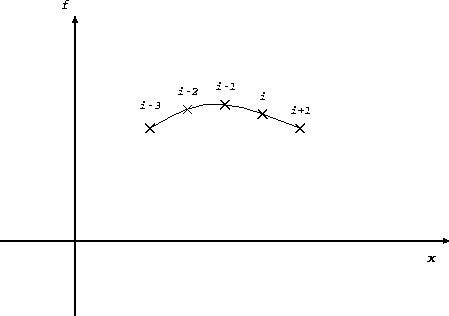
上の図に概念を示す。ここでは、ラグランジュ補間 （ニュートン補間）をして多項式を作る。で、その作った多項式を積分する。 例えば、点 i から i+1まで積分するのに、点 i-p から iまでの関数 値を使うとすれば、p次の多項式で
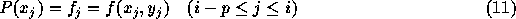
を満たすものを作る。で、i+1での解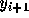 
は
で与えられる。 刻み hが定数であるとすれば、pを決めれば上の式を
の形に書き直せる。
簡単な例として、 p = 1の場合を考えてみよう。この時、補間多項式は一次 であって
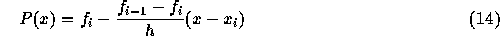
となって、これを積分すれば、結局
となる。
一般に、アダムス法では任意段数の公式が構成でき、その次数は段数に等しい ことがわかっている。これは、ルンゲ・クッタなどに比べればはるかによい性 質をもっているということでもある。
アダムス法はいくらでも高次の公式が作れ、計算量もあまり多くないというこ とがわかっているが、必ずしも広く使われているというわけでもない。その理 由はいろいろあるが、一つは、
「どうやって計算を始めるべきかよくわからない」
ということである。つまり、初期値問題としてはもちろん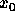 
における
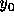しか知らないのに、多段階法ではその前の時刻での解が必要になるわけ
である。これに対する対応策はいくつかあるが、時間刻み一定の場合には、基
本的にはルンゲ・クッタなどの別な方法で解を求めておくというやりかたが普
通である。
というわけで結局プログラムを書く手間が2倍以上になるというのが、多段階 法の実用上の問題である。
さて、前に述べた公式では、補間多項式を陽的に求めた。すなわち、時刻 i
とそれより以前の値だけを使っていた。これに対し、陰的な補間多項式、つま
り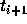 
での関数の値を使った公式というものも考えられる。
刻み hが定数であるとすれば、pを決めれば前と同様に
の形に書けることになる。また手をぬいて p=1の場合を考えれば、これは単 に台形公式
となる。
陰的公式の場合、例によってどうやって代数方程式を解くかが問題になる。通 常の方法は、
なお、このやり方を、予測子・修正子法と呼ぶ。線形多段階法はほとんどこの 形で使われるため、線形多段階法のことをさして予測子・修正子法と呼ぶ人も いる。