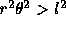7 力の計算

さて、このように木構造ができてしまうと、実際の力の計算は非常に簡単にな る。以下が力を計算する関数である。

pt minus 1 pt

void bhnode::accumulate_force_from_tree(vector & ipos, real eps2, real theta2,
                                        vector & acc,
                                        real & phi)
{
    vector dx = pos - ipos;
    real r2 = dx*dx;
    if ((r2*theta2 > l*l) || (nparticle == 1)){
        accumulate_force_from_point(dx, r2, eps2, acc, phi, mass);
    }else{
        for(int i=0;i<8;i++){
            if (child[i] != NULL){
                child[i]->accumulate_force_from_tree(ipos,eps2,theta2, acc, phi);
            }
        }
    }
}

これはメンバ関数になっていて、あるノードから引数で渡ってくる場所への力 （加速度）とポテンシャルを計算する（渡ってきた変数に足し込む）。距離の 2乗を計算し、それが 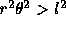を満たしていれば実際に加速度を 計算する。2乗のままで比べるのは、単に平方根計算をしないですませるためである。 また、粒子数が1であればやはり同様に加速度を計算する。そうでなければ、 子ノードを順番にみて重力を計算する。ここでも再帰をつかう。

質点からの力、ポテンシャルの計算は以下のようになる。

pt minus 1 pt

void accumulate_force_from_point(vector dx, real r2, real eps2, 
                                 vector & acc,
                                 real & phi,
                                 real jmass)
{
    double r2inv = 1/(r2+eps2);
    double rinv  = sqrt(r2inv);
    double r3inv = r2inv*rinv;
    phi -= jmass*rinv;
    acc += jmass*r3inv*dx;
}

ベクトル型というのを作っておいたので、記述が簡潔になっていることがわか る。