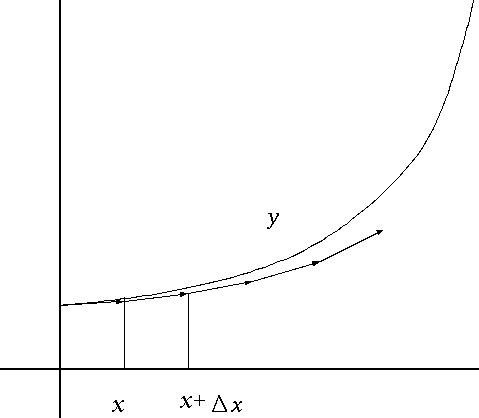
この、線形の方程式の場合にはもちろん解析的に解けるので、数値解を計算したりする必要はない。しかし、非線形で解析解がない問題というのは無数にあり、そのときにこのような数値的な近似は強力な手段となる。
時間の関係があるので偏微分方程式は扱わない。
なお、これは無記名ですので、成績評価に影響することはありません。また、講義に関する要望、意見などがあったら、自由にマークカードの裏に書いて下さい。
program ode1(input, output);
var x, xend, dx, y, k : real;
begin
write('Enter k, y0, xend, dx:');
readln(k, y, xend, dx);
x := 0;
while x <= xend do begin
y := y + dx*k*y;
x := x + dx;
writeln('x, y = ', x:20:10,' ', y:20:10);
end;
end.
上の例は、一階線形常微分方程式の初期値問題

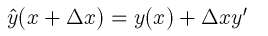
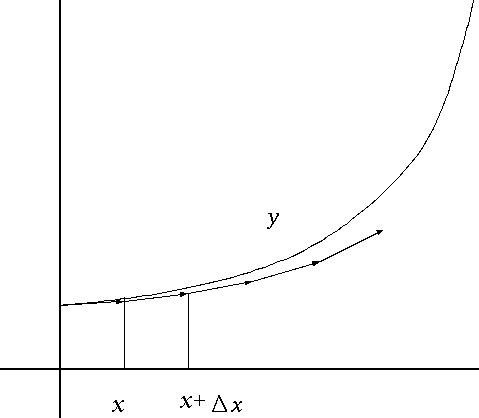
この、線形の方程式の場合にはもちろん解析的に解けるので、数値解を計算したりする必要はない。しかし、非線形で解析解がない問題というのは無数にあり、そのときにこのような数値的な近似は強力な手段となる。
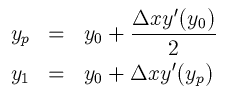
program ode_system(input, output);
const nvar = 2;
type vector = array[1..nvar] of real;
var i : integer;
y : vector;
x : real;
xinit, xend, dx : real;
procedure calculate_dy(x: real; y : vector; var dy : vector);
begin
dy[1] := y[2];
dy[2] := -y[1];
end;
procedure integrate(var y : vector; var x : real; dx : real);
var yp,dy : vector;
i : integer;
begin
calculate_dy(x,y,dy);
for i:=1 to nvar do yp[i] := y[i]+0.5*dx*dy[i];
calculate_dy(x,yp,dy);
for i:=1 to nvar do y[i] := y[i]+dx*dy[i];
x := x + dx;
end;
begin
write('Enter xend, dx: ');
readln(xinit, xend, dx);
y[1]:=0;
y[2]:=1;
x := 0;
while x < xend do begin
integrate(y, x, dx);
write(x:16:7);
for i:= 1 to nvar do write(' ',y[i]:15);
write(y[1]-sin(x), y[2]-cos(x));
writeln;
end;
end.
このプログラムは、(手続き calculate_dy の中身さえ書き換えれば)
どのような連立常微分方程式でも解くことができる(はずである)。
今までに使ったことのない Pascal の言語機能としては
const nvar = 2; type vector = array[1..nvar];の
プログラムでやっていることは、手続き、配列を使っていることの他は上でやっ
た1変数常微分方程式とあまり違わない。
台形公式は、計算量が増えるという欠点はあるが、重要な特長がいくつかあり、
この方法を発展させた様々な方法が広く用いられている。
なお、常微分方程式の数値解法については、問題の性質に応じたさまざまな方
法が研究され、実用化されている。興味がある人は、
牧野が教養学部広域科学科でしている講義とか、そのなかで紹介している
参考文献をみてみるのもいいかもしれない。
台形公式
procedure integrate(var y : vector;
var x : real;
dx : real);
var y1,dy0,dy1 : vector;
i,k : integer;
begin
calculate_dy(x,y,dy0);
for i:=1 to nvar do y1[i] := y[i]+dx*dy0[i];
for k:=1 to 3 do begin
calculate_dy(x,y1,dy1);
for i:=1 to nvar do y1[i] := y[i]+0.5*dx*(dy0[i] + dy1[i]);
end;
for i:=1 to nvar do y[i] := y1[i];
x := x + dx;
end;
台形公式は、ルンゲ・クッタ公式と同様に高い精度が得られる。この方式の特徴は
y1 = y + 0.5*dx*(dy0 + dy1)
としているところで、 dy1 が実は y1 の関数になっているところである。こ
のために、ここでは前回やった「直接代入法」で、 y1 についての方程式を解
いている。ただし、 答が正しく求まったかどうかの判定はしないで、最初の
値(オイラー法でもとめた)から数回(この例では3回)繰り返して打ちきっ
ている。グラフィック
begin
write('Enter xend, dx: ');
readln(xend, dx);
y[1]:=0;
y[2]:=1;
x := 0;
initgraph(gdriver, gmode, '');
moveto(400+round(200*y[1]),400-round(200*y[2]));
while x < xend do begin
integrate(y, x, dx);
lineto(400+round(200*y[1]),400-round(200*y[2]));
end;
readln;
end.
メインプログラムを上のように書き換えると、数値積分した答をグラフィック
表示することができる。(練習
独立変数を横軸、一変数高階微分方程式
一般に、高階微分方程式 f(x,y,y',y'',y''' ,...) = 0 の数値解は、最高次の次数を
nとして以下のように計算できる:

例:強制振動
例えば強制振動の方程式
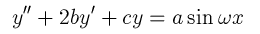
は、以下のように
(省略)
a, b, c,omega : real;
procedure calculate_dy(x : real;y : vector; var dy : vector);
begin
dy[1] := y[2];
dy[2] := -2*b*y[2] -c*y[1] + a* sin(omega*x);
end;
(省略)
begin
write('Enter xinit, xend, dx: ');
readln(xinit, xend, dx);
write('Enter a, b, c, omega ');
readln(a, b,c, omega);
y[1]:=1;
y[2]:=0;
x := xinit;
initgraph(gdriver, gmode, '');
moveto(400+round(200*y[1]),400-round(200*y[2]));
while x < xend do begin
integrate(y, x, dx);
lineto(400+round(200*y[1]),400-round(200*y[2]));
end;
readln;
end.
練習
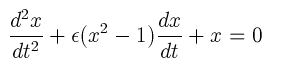
をプログラムしてみよう。これは非線形振動(自励振動)のもっとも簡単なモ
デルの一つである。
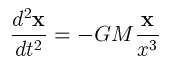
をプログラムしてみよう。例えば y[1] を x, y[2] を v_x,
y[3] を y, y[4] を v_y とおき、 calculate_dy を書き
直す。また、 nvar=4 とする。

をプログラムして、数値解を求めてみよう。また、定常状態はどこか?