講義第11回：Pascal プログラミング --- 再帰

再帰

もっとも簡単な例

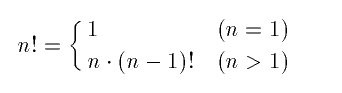
program recursion_sample(input, output);
var n : real;

    function factrial(n :real): real;
    begin
        if n=1.0 then begin
            factrial := 1.0;
        end else begin
            factrial := n*factrial(n-1);
        end;
    end;
begin
    write('Enter n : ');
    readln(n);
    writeln('N = ', n:5, ' N! = ', factrial(n):20);
end.

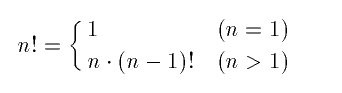
Pascal のようなプログラミング言語では、この定義に従って素直にプログ ラムを書くことができる。上の例では、まさに、 n が 1 なら 1 を返 し、それ以外では n*factrial(n-1)を返すというのが、 factrial(n)の中身になっている。 例えば factrial(5) を計算させるとすると、実際の計算は、以下のよ うな手順で進む。

factrial(5)
→5*factrial(4)
→5*(4*factrial(3))
→5*(4*(3*factrial(2)))
→5*(4*(3*(2*factrial(1))))
→5*(4*(3*(2*1)))
→5*(4*(3*2))
→5*(4*6)
→5*24
→120

練習

1. 階乗を計算する関数を、再帰を使わない形に書き直してみよ。
2. ある程度大きな数の階乗は正しく計算できない。計算できるのはい くつまでか。またそれより大きな数を入れた時にでる答えはどういう意味があ るか。
3. フィボナッチ数列$F(n) = F(n-1) + F(n-2), F(0)=0, F(1)=1を再 帰、再帰でないものの両方を使って書け。なお、変数には real または double を使うこと。
4. 上のフィボナッチ数列について、n を大きくしていった時に計算の手間が どのように増えるかを、再帰の場合とそうでない場合のそれぞれについ て考察せよ。

お絵書き

program tree_display(input, output);
#include <xgraph.h>
var gdriver, gmode : integer;
    x,y,vx,vy      : real;
    i,j            : integer;
    procedure tree(n, x, y: integer; angle, length : real);
    var x1, y1 : integer;
    begin
        if n > 0 then begin
            setcolor( n mod 7 + 1);
            x1 := round(x + length*cos(angle));
            y1 := round(y - length*sin(angle));
            line(x,y,x1,y1);
            tree(n-1,x1,y1,angle + 0.25, length*0.7);
            tree(n-1,x1,y1,angle - 0.25, length*0.7);
        end;
    end;
begin
    initgraph(gdriver, gmode, '');
    cleardevice;
    clrscr;
    tree(10, getmaxx div 2, getmaxy, pi/2, getmaxy  div 4);
    readln;
    closegraph;
end.

再帰を使うことで、角度、長さを変えて自分自身を呼び出すという形で簡潔に アルゴリズムが表現できている。

練習

1. この木では、枝が2本ずつ出ているが、もっとたくさん出すにはどうすればい いだろうか？
2. この木は枝分かれが完全に規則的で不自然である。自然にするにはどうすれ ばいいだろうか？
   （ヒント：random(x) --- x は実数 --- という関数を呼ぶと、0 から x まで の範囲の乱数 --- デタラメな数 --- を返す。これを使って枝分かれの長さ、 角度を変えて見よう)
3. 以下に示すようなフラクタル図形も、うえのプログラムと同じよう な考え方で作ることができる。どのようにすればいいかを考えて、 プログラムを作ってみよ。
   
   

ソート（２）

配列のところ（前回）でやったソーティングについて考えてみる。

上の方法では、人間がやるとしたらとてもばかばかしくてできないような、手 際の悪い方法をつかっている。このために、手間がデータの数の2乗に比例し て増える。これを、もう少しなんとかできないものだろうかというのがここで の課題である。

例えばトランプのカードを人が揃えるとすれば、一つの方法は、まずハート、 スペードといった種類ごとに分け、それからその中を揃えることである。こう すれば、枚数が減って扱いやすい。

もう一つの考え方は、まず揃ってない山を2つに分け、それぞれを揃える。そ れからその2つを合体させるというものである。合体させるのは、両方の山を みて順番が先なものをとっていけばいい。

どちらの方法でも、カードの山をいくつかに分けることで、手間を減らしてい ることがわかる。ここで、よく考えてみると、例えば下の方法では、初めに2 つに分けた山のそれぞれを揃えるのに、さらにそれらを2つに分けるという方 法が使えることが分かる。上の方法でもおなじようなことができる。

この、同じ方法を繰り返し使うというのが、「再帰」の考え方である。具体例 を見てみよう。

program mergesort(input, output);
var n   : integer;
    data: array[1..100] of real;
    wa  : array[1..100] of real;
    i,j : integer;
    infile:text;
    procedure merge(if1, ie1, if2, ie2:integer);
    var i, j, k : integer;
    begin
        i := if1;
        j := if1;
        k := if2;
        while (j <= ie1) or ( k <= ie2) do begin
            if (j > ie1) or ((k <= ie2) and (data[k] < data[j])) then begin
               wa[i] := data[k];
               k := k + 1;
            end else begin
               wa[i] := data[j];
               j := j + 1;
            end;
            i := i + 1;
        end;
        for i := if1 to ie2 do data[i] := wa[i];
    end;
    procedure msort(ifirst, iend:integer);
    var i : integer;
    begin
        i := (ifirst + iend) div 2;
        if ifirst < i then msort(ifirst, i);
        if i+1 < iend then msort(i+1, iend);
        merge(ifirst, i, i+1, iend);
    end;
procedure print(n:integer);
    var i : integer;
    begin
        for i:= 1 to n do begin
            write(' ', data[i]:9:2);
            if i mod 8 = 0 then writeln;
        end;
        if n mod 8 <> 0 then writeln;
    end;
begin
    n := 0;
    while not eof(input) do begin
        n := n +1;
         readln(input, data[n]);
    end;
    writeln('Input data'); print(n);
    msort(1,n);
    writeln('Sorted data');print(n);
    readln;
end.

1. まず、データを前半分と後ろ半分にわけ、それぞれソートしておく。

2. その2つを、それぞれ先頭からみて小さい方をとって並べていく。

1. のところを行なうのが、手続き msort の前半部である。これは、 前半分と後ろ半分について、それぞれ msort 自身を呼ぶ。

2. のところは、手続き merge で行なわれる。ここでは、 dataの if1 から ie1 までと、 if2 か ら ie2 までに入っている２つの部分列を、１つの列にまとめる。 この時、いったん wa という配列に書いておいて、終ったところで 書き戻す。

merge の動く様子

列a 1 3 4 8 9 列b 2 4 6 7 8 合併列 （空）
列a 3 4 8 9   列b 2 4 6 7 8 合併列 1
列a 3 4 8 9   列b 4 6 7 8   合併列 1 2
列a 4 8 9     列b 4 6 7 8   合併列 1 2 3

再帰という形に書くことで、高度な処理を単純な形に表現することがで きる。これについては次週にもう少し詳しく学ぶことにする。

練習

1. 教科書のクイックソートのプログラムを実行してみて、うまく動くこ とを確認してみよ。また、なぜこれでうまくいくかを考えよ。

2. データの数を非常に大きくした時、実行時間がどうなるかを単純ソート プログラムと再帰を使うものの両方について測定せよ。配列宣言の数字を大き くするのを忘れないこと。また理論上どうなるはずか考えてみよ。

time simple_sort < sample.dat

0.040u 0.080s 0:00.56 21.4% 0+135k 2+0io 21pf+0w

レポート

• プログラム
• 実行結果
• 考察

理科II 3,5,6,7 組： cc76813
理科II 9,10 組： cc76826
他クラス： cc76826
	    

次回予告