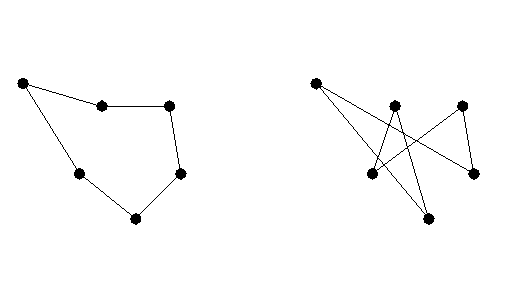
上に、最短距離の例と、そうでない例を示す。 もちろん、都市のすべての順列について道のりを調べて、もっとも短いものを とれば正しい答が求まる。しかし、これはには都市の数の階乗くらいの手間が 掛かるので、10個くらいから先は、速い計算機をつかってももう現実的とはい い難い。
しかし、もちろん、計算機の中ではこの逆三角関数を何らかの方法で計算して 求めているわけである。求め方は様々であるが、ここでは野蛮な、その代わり に適用範囲の広い方法を考える。
原理は以下のようなものである。正方形の中に一様に分布するような乱数を発 生させる。で、正方形の中に円を書いておいて、発生させた乱数の中でその中 に落ちたものの数を数える。これと発生させた乱数の数を比べれば、これは発 生させた乱数の数を無限大に持っていった極限で、正方形と円の面積の比にな る。したがって、有限回の試行でも、πの近似値が求められるはずである。 以下にプログラムを書いてみる。
program capculate_pi(input,output);
var n, ndisp : integer;
var x,y, p, pi : real;
var i,count : integer;
function drand48 : double; external;
begin
write('enter nmax:');
readln(n);
ndisp := 2;
count := 0;
pi := arctan(1.0)*4.0;
for i :=1 to n do begin
x := drand48;
y := drand48;
if (x *x + y*y) < 1.0 then count := count + 1;
if i = ndisp then begin
p := (count *4.0)/i;
writeln('i, pi, err = ', i, p, p-pi);
ndisp := ndisp * 2;
end;
end;
end.
これは、試行回数が2倍になる度にπの近似値を出力するよ
うになっている。もちろん、これは、πを計算するもっとも能率のいい方法というわけではない。 現在、πの値は数十億桁まで計算されている(もっとも先まで求めたのは、東 大大型計算機センターの金田先生である)が、こういった計算には、繰り返し 計算するとπに収束するような特殊な数列を使っている。
また、一般に、ある関数 f(x) があって、その定積分を数値的に求めるという 場合でも、上の方法よりずっと能率のいい方法(台形公式、シンプソン公式な ど)がある。
しかし、上の方法には、メリットがないわけではない。例えば、非常に複雑な 図形の体積を求めるといったことを考えてみる。上の方法では、「座標を与え て、その図形のなかにあるかどうかを判定する」関数さえ作れば、あとは時間 さえ書ければいくらでも正確な体積が計算できる。しかし、曲面に囲まれた体 積を例えばシンプソンの公式で求めるのは、それほど簡単な話ではない。
これにたいし、上の方法では多次元でもなんでも単純なプログラムで計算する ことができる。上のような方法のことを一般にモンテカルロ法という。
なお、
function drand48 : double; external;は、この計算機システムで準備されている drand48 という関数を使うという 宣言である。 drand48 がどういうものかは man drand48 で見ることができる。
ここで考えるのは、「巡回セールスマン問題」と呼ばれる問題である。これは、 要するに、セールスマンがいくつかの都市を回るのに、最短距離で回るにはど うすればいいかという問題である。

上に、最短距離の例と、そうでない例を示す。
もちろん、都市のすべての順列について道のりを調べて、もっとも短いものを
とれば正しい答が求まる。しかし、これはには都市の数の階乗くらいの手間が
掛かるので、10個くらいから先は、速い計算機をつかってももう現実的とはい
い難い。
そこで、乱数を使うわけだが、まず、「乱数を使って順番を決めて、短いのが できたらそれを答として採用する」という方法が考えられる。これは、残念な がら、あまりうまくいかない(興味がある人は実際にやってみること)。
これよりずっとましなのは、まず適当な順番からはじめて、ランダムに順番を 入れ換えてみて、前よりも短くなったらそれにするというのを繰り返すという 方法である。しかし、これでも、非常に良い答えには必ずしもいかない。
ここで、しかし、順番を入れ換えた後、道のりが伸びてしまったとしても一定 の確率でそっちに置き換えることにし、その代わり置き換える確率を段々減ら していくことにすると、非常に良い答えに到達できるということが知られてい る。
このような方法を、simulated annealing (模擬焼きなまし)という。焼きな ましとは、物を加熱しておいて、ゆっくり冷やしていくことである。
これは、なんだかいい加減な方法に見えるかも知れないが、熱力学 (統計力学)と関係付けることができ、ちゃんとした理論体系がある。
ある物体を、有限温度からはじめて「十分にゆっくり」冷やしていくと、絶対 零度になった時にその系のとりうるエネルギーの最小状態になるということが 知られている。これに対し、十分ゆっくりでないと、具合の良くない状態のま ま固まってしまって、エネルギー最小状態までいかない。
巡回セールスマン問題のような、非常に変数の数の多い関数の最大値/最小値 をもとめる問題は、この関数が物理系をあらわしている(もっともらしくいえ ば、系のハミルトニアンになっている)と考えると、理論的には上の「焼きな まし」によって厳密な答を求めることができる。
実際には、厳密な答を求めるためには非常にゆっくり冷やさないといけないが、 まあある程度急速に冷やしてもそこそこの答えは求まるということが知られて いる。
というわけで、プログラムを示す。
program travelling_salesman(input,output);
#include <xgraph.h>
function drand48: real; external;
const ncmax = 500;
type coordinate = array[1..2] of real;
type index_type = array[1..ncmax] of integer;
var cities : array[1..ncmax] of coordinate;
index : index_type;
function distance(x1,x2 : coordinate ): real;
var dist2 : real;
begin
dist2 := sqr(x1[1]-x2[1]) +sqr(x1[2]-x2[2]);
distance := sqrt(dist2);
end;
function length(ncities : integer;ind:index_type ) : real;
var sum : real;
i : integer;
begin
sum:= 0;
for i:=1 to ncities - 1 do
sum := sum + distance(cities[ind[i]],cities[ind[i+1]]);
length := sum + distance(cities[ind[ncities]],cities[ind[1]]);
end;
procedure generate_cities(ncities: integer);
var i : integer;
begin
for i:= 1 to ncities do begin
cities[i][1] := drand48;
cities[i][2] := drand48;
end;
end;
procedure display_cities(ncities: integer);
var i : integer;
begin
cleardevice;
moveto( round(cities[index[ncities]][1]*800),
round(800-cities[index[ncities]][2]*800));
for i:=1 to ncities do begin
lineto( round(cities[index[i]][1]*800),
round(800-cities[index[i]][2]*800));
end;
end;
procedure change_and_test(t: real; ncities:integer);
var newindex : index_type;
i,j,k : integer;
oldsum, newsum,x : real;
accept : boolean;
begin
oldsum := length(ncities, index);
repeat
i := round(drand48*ncities + 0.5);
j := round(drand48*ncities + 0.5);
until i < j;
newindex := index;
for k:=i to j do newindex[k] := index[j-k+i];
newsum := length(ncities, newindex);
accept := false;
if newsum < oldsum then begin
accept := true;
end else begin
x := drand48;
if x < exp(-(newsum - oldsum)/t) then accept := true;
end;
if accept then begin
index := newindex;
end;
end;
var ncities,i : integer;
gmode, gdriver : integer;
t0, dt, tend, t : real;
niter : integer;
begin
write('enter ncities:');
readln(ncities);
initgraph(gdriver, gmode, '');
for i:=1 to ncities do index[i] := i;
generate_cities(ncities);
display_cities(ncities);
writeln('enter t0, dt, tend, niter:');
readln(t0, dt, tend, niter);
t := t0;
while t > tend do begin
for i := 1 to niter do change_and_test(t,ncities);
display_cities(ncities);
writeln('t, length=', t, length(ncities, index));
t := t * dt;
end;
readln;
end.
cities と index は、それぞれ都市の位置座標とそれらを回る順番をあらわ す。メインプログラムでは、まず都市の数を入力し、乱数で座標を発生させる。 (実際の問題に使うのならば、ここで入力ファイルから読み込む)
次に、 index はまず 1,2,.... という順にしておき、画面にどんな風になっ ているかを表示する。 (display_cities)
次に、繰り返しのパラメータを読み込む。上に述べた理由で、「温度」という 概念が入ってくるので、パラメータは、最初の温度、温度の下げ方、最後の温 度、ある温度で順番を変えてみる回数の4個である。
以下、実際に順番を変えてみて、それを採用するかどうかを判定するのが change_and_test である。
順番の変え方は、まず都市を2個ランダムに選んで、その間の順番をひっくり 返す。選んだところで切ってつなぎかえていることになる。
4 3 1 2 7 6 5 8
^ ^
4 3 6 7 2 1 5 8
上に、都市の数が8だったとして、3, 6 が選ばれた時にどのように並び代わる
かというのを示す。この、並び変えた順番は newindex にしまっておき、これでぐるっと回った道 のりを計算する。これは、単に隣合わせの都市間の距離を計算し、足していく だけである。
新しい道のりと古い道のりで、新しいのが短くなっていれば accept という変
数(ブーリアン、つまり論理値をとる)を真にしておく。そうでなければ、ま
ず0 と1の間の一様乱数を発生させ、これと、
温度 t が大きければ、newsum と oldsum の差が大きくても確率が小さくなら ない。これにたいし温度 t が小さいと、newsum と oldsum の差が大きいと確 率が急速に小さくなる。
accept が真になったら、 index に newindex をコピーする。
あとはこれを繰り返し、所定の回数になったら t を小さくしてまた繰り返し、 所定の温度になるまで続けるだけである。
このような trial-and-error 的な方法は、最近になって様々な問題に広く適 用され、研究が進んでいる。生命の進化も、このような、ランダムな遺伝子の コピー間違いと生存競争(確率的なものも入る)で理解できると考えられてい る。実際に人工生命の研究では、上のような方法で人工生命を「進化」させる。
これは出さなくても構わないが、試験の出来が心配な人は出しておいた方がい いかもしれない。