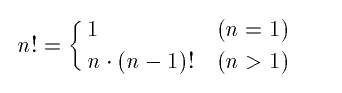
program recursion_sample(input, output);
var n : real;
function factrial(n :real): real;
begin
if n=1.0 then begin
factrial := 1.0;
end else begin
factrial := n*factrial(n-1);
end;
end;
begin
write('Enter n : ');
readln(n);
writeln('N = ', n:5, ' N! = ', factrial(n):20);
end.
上の例
は、階乗を計算するプログラムである。階乗は、下のように定義される:
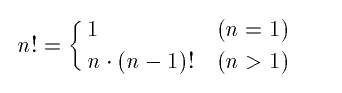
Pascal のようなプログラミング言語では、この定義に従って素直にプログ
ラムを書くことができる。上の例では、まさに、
再帰を使うことで、角度、長さを変えて自分自身を呼び出すという形で簡潔に
アルゴリズムが表現できている。
これは、以下のようなプログラムで実現できる。
これに対し、直接代入法では、ほとんど何も考えなくてもプログラムが
作れる。もちろん、答が求まるための条件がつくが、様々な実用上の問
題で結構うまく求めることができる。
factrial(5)
→5*factrial(4)
→5*(4*factrial(3))
→5*(4*(3*factrial(2)))
→5*(4*(3*(2*factrial(1))))
→5*(4*(3*(2*1)))
→5*(4*(3*2))
→5*(4*6)
→5*24
→120
練習
お絵書き
再帰を使って複雑な図形を書いてみよう。
program tree_display(input, output);
#include <xgraph.h>
var gdriver, gmode : integer;
x,y,vx,vy : real;
i,j : integer;
procedure tree(n, x, y: integer; angle, length : real);
var x1, y1 : integer;
begin
if n > 0 then begin
setcolor( n mod 7 + 1);
x1 := round(x + length*cos(angle));
y1 := round(y - length*sin(angle));
line(x,y,x1,y1);
tree(n-1,x1,y1,angle + 0.25, length*0.7);
tree(n-1,x1,y1,angle - 0.25, length*0.7);
end;
end;
begin
initgraph(gdriver, gmode, '');
cleardevice;
clrscr;
tree(10, getmaxx div 2, getmaxy, pi/2, getmaxy div 4);
readln;
closegraph;
end.
これは、樹形図を書くプログラムである。原理は、指定した長さと角度で一本
線を引き、その先から角度をつけて2本線を引き、それぞれの端からまた角度
をつけて、、、というのを繰り返すだけである。練習
(ヒント:random(x) --- x は実数 --- という関数を呼ぶと、0 から x まで
の範囲の乱数 --- デタラメな数 --- を返す。これを使って枝分かれの長さ、
角度を変えて見よう)

代数方程式
2週前に、2分法で方程式の数値解を求める方法について学んだ。今回は、
2つの違った方法について学び、その間の優劣について考える。
ニュートン法 (Newton-Raphson method)
二分法では、繰り返し一回毎に区間が半分、つまり近似解の精度が2倍になる。
従って、例えば10桁の精度が欲しければ、 10/log 2 〜 33 回計算を
繰り返す必要がある。多くの実用的な問題では、この程度の繰り返し回数は問
題にならないが、場合によってはもっと早く正確な答が欲しい時もある。その
ような時に有用なのがニュートン法である。
program newton_raphson(input, output);
var x, f, df: real;
begin
x := 1.0;
repeat
f := cos(x) - x;
df:= -sin(x) - 1.0;
x := x - f/df;
writeln('x=', x:20:16, ', cos(x)-x=', f);
until abs(f) < 1e-10;
end.
ニュートン法では、近似解のところで関数の接線をひき、それと軸との
交点を新しい近似解にする。 y=f(x)の x=x0での接線の方程式は
y=f(x_0)+f'(x0)(x-x0)$なので、x軸との交点は x = x0 -f(x0)/f'(x0)
になるわけである。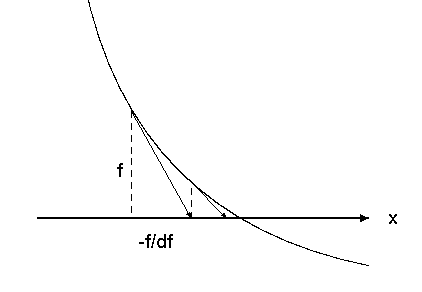
実行例
x= 0.7503638678402439, cos(x)-x=-4.59697694131860e-01
x= 0.7391128909113617, cos(x)-x=-1.89230738221174e-02
x= 0.7390851333852840, cos(x)-x=-4.64558989907715e-05
x= 0.7390851332151607, cos(x)-x=-2.84720580445708e-10
x= 0.7390851332151607, cos(x)-x= 0.00000000000000e+00
練習
直接代入法
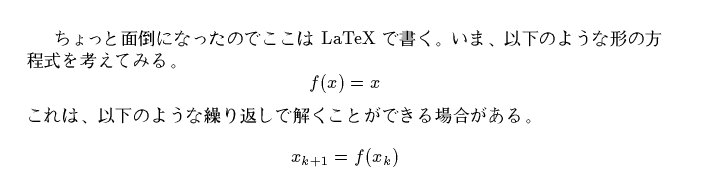
program direct_iteration(input, output);
var x, xold: real;
begin
x := 1.0;
repeat
xold := x;
x := cos(x) ;
writeln('x=', xold:20:16, ', x-cos(x)=',xold-x:20:16 );
until abs(x-xold) < 1e-10;
end.
練習
3つの方法の優劣について簡単にまとめておく。
「プログラムが簡単である」というのは意外に重要な性質である。これ
までは1変数の方程式を考えていたが、多変数の方程式を解く場合
を考えてみよう。2分法はどうすれば多変数に拡張できるか良くわからな
い。ニュートン法は、原理としては簡単に多変数に拡張できる。
しかし、連立一次方程式を解くこと自体それほど簡単ではないし、また、
すべての偏導関数を計算するプログラムを作るのも結構厄介である。次回予告
次回は、シミュレーション(時間発展する方程式の数値解を求める)の
手法について学ぶ。