./note010.html

ToC

10. HPL 書き直し (2009/9/2 書きかけ)

別のところに書いたような事情で、 HPL を書き直してます。とりあえず MPI とか並列化は後回しで、どういうメモリレイアウトやチューニングをするか、を1ノードの短いプログラムで調べています。

普通に Top500 で使われている HPL は、行列のデータ格納の順序が Column Major (列優先)というもので、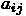のが変わるものが連続アドレスに入ります。これは、ピボット探索ではメモリフットプリントが最小になるし、また昔からある普通の縦ブロックガウスでキャッシュ(昔ならディスクでない主記憶自体))を有効に使うという話であれば、これを逆転させて Row Major (行優先)にする、というのは全くありえない話です。

が、行列乗算にアクセラレータを使い、またそのためのブロック化に Gustavson の再帰的ブロッキングとかを使うと話が変わってきます。まず、行列乗算の効率を上げるために right-looking にするので、ここに関しては縦長の行列と横長の行の積となり、行優先でも列優先でも同じです。再帰的パネル分解では縦長の行列と小さな正方行列の積(結果は縦長)となるので、これは列優先のほうが若干得ですが、行列サイズが極端に小さい(幅がキャッシュラインサイズ以下になる)場合でなければ大きな性能差はでないでしょう。

right-looking の場合には、右側に残っている部分正方行列全体に対して、部分ピボットの結果でてくる行交換を行う必要があります。この部分は列優先では非常に不利で、どうやってもキャッシュラインの殆どが無駄になります。

さて、では、ピボット探索と行交換の両方を高速にするのは不可能か、というと、縦方向に再帰分解をしているわけなので、適当なサイズのところで転置すればよいはずです。転置のための余計なメモリアクセスが発生するわけですが、

転置後の列優先行列はキャッシュに入る

転置前に行列の幅はキャッシュラインサイズ以上

というのを同時に満足できれば、メインメモリからは行列半分を読み出して半分を格納、となります。また、転置はその領域を更新する行列乗算の直後に起こるので、行列乗算ルーチンが結果をキャッシュに残していれば(これは、 moventpd を使わない、ということでもありますが)、高い性能が期待できます。ということで、まだ GRAPE-DR を使っていないしシングルコアのコードですが、転置を行うものを書いてみました。これは、8列になったところで転置します。また、最大のブロックサイズは 64 です。N=2K で、 Athlon 64 X2 4050e でのプロファイルの結果が以下です。実際の実行時間は 1.8秒だったので、下の時間速度はあまり正確ではありませんが、相対値には意味があるかな？という程度です。

 Each sample counts as 0.01 seconds.
   %   cumulative   self              self     total           
  time   seconds   seconds    calls  ms/call  ms/call  name    
  86.41      1.27     1.27                             dgemm_kernel
   2.72      1.31     0.04      256     0.16     0.16  transpose_coltorow
   2.04      1.34     0.03                             dgemm_otcopy
   1.36      1.36     0.02     8192     0.00     0.00  swaprows
   1.36      1.38     0.02        1    20.00    20.00  copymats
   0.68      1.39     0.01     4096     0.00     0.00  vvmulandsub
   0.68      1.40     0.01     1024     0.01     0.01  column_decomposition
   0.68      1.41     0.01      256     0.04     0.04  solve_triangle
   0.68      1.42     0.01      256     0.04     0.04  transpose_rowtocol
   0.68      1.43     0.01      193     0.05     0.05  matmul_for_small_nk
   0.68      1.44     0.01        1    10.00    10.00  backward_sub
   0.68      1.45     0.01                             dgemm_beta
   0.68      1.46     0.01                             dgemm_nn
   0.68      1.47     0.01                             dgemm_oncopy

copymats は初期の行列をコピーする関数で、ソルバの時間にははいりません。 dgemm 以外で無視できない時間を占めるのは

 transpose_coltorow   列優先から行優先に戻す
 swaprows             行交換
 vvmulandsub          ベクトル同士の外積 
 column_decomposition 再帰の最後のパネル分解
 solve_triangle       3角行列の求解
 transpose_rowtocol   行優先から列優先に転置
 matmul_for_small_nk  行優先の状態での縦長な行列と小さな行列の乗算

といった辺りです。参考のために、 single core での STREAM の実行結果は

 Function      Rate (MB/s)   RMS time     Min time     Max time
 Copy:        4096.5704       0.0500       0.0500       0.0504
 Scale:       2506.7073       0.0818       0.0817       0.0829
 Add:         3410.3011       0.0901       0.0901       0.0901
 Triad:       3247.1131       0.0946       0.0946       0.0947

というところです。これは、moventpd イントリンシックを使ったもので、 Triad では

        for (j=0; j<N/2; j++)
            //      a[j] = b[j]+scalar*c[j];
            __builtin_ia32_movntpd((double*)&av[j], bv[j]+ss*cv[j]);

というようなコードです。Scale が極端に遅いですが、まあ 3-4GB/s がメモリの実力です。

まず、一番上の行列転置 transpose_coltorow ですが、行列全体は 32MBで、そのうち半分が転置に関係するので 16MB、これを 0.04 sec でなんとかしているので速度は 400MB/s で、話にならないほど遅いので明らかに工夫が必要です。swaprows は交換のためにには 2回読んで書く必要があり、それでも半分の時間でおわっているのでまあよいような気がします。

上のテストで転置に使ったのは

 void transpose_coltorow(int n, double a[][RDIM],int m, double at[][n],
                        int istart)
 {
     int i,j;
     for(i=istart;i<n;i++)
        for(j=0;j<m;j++)
            a[i][j] = at[j][i];
 }

という全くなんの芸もないコードです。こんなのでは駄目に決まっているので、色々改良してみます。まずはブロック化です。一旦、 m x m の正方行列に転置しながらコピーして、それを連続アクセスでコピー、としてみます。

 void transpose_coltorow(int n, double a[][RDIM],int m, double at[][n],
                        int istart)
 {
     int i,j,k;
     double atmp[m][m];
     for(i=istart;i<n;i+=m){
        for(j=0;j<m;j++){
            for(k=0;k<m;k++){
                atmp[k][j]  =at[j][i+k];
            }
        }
        for(k=0;k<m;k++){
            for(j=0;j<m;j++){
                a[i+k][j] = atmp[k][j];
            }
        }
     }
 }

これの結果は

  0.65      1.52     0.01      256     0.04     0.04  transpose_coltorow

というところで、測定精度があまりありませんが遅くなってはいません。後半のコピーで、 moventpd を使ってみると

            v2df * atp = (v2df*) atmp[k];
            for(j=0;j<m;j+=2)
                __builtin_ia32_movntpd(a[i+k]+j, atp[j/2]);

という感じです。これは速いか、というと、

  0.00      1.51     0.00      256     0.00     0.00  transpose_coltorow

となって確かに速いのですが、全体の実行時間は必ずしも短くはなりません。これは、moventpd では代入した結果がキャッシュに残らないのですが、実際には代入した結果はそのあとすぐに使うので、どうせまたキャッシュにはいってくるからです。これは行列優先から列優先への転置でも同じで、movntpd を使うとこの関数自体は速くなったように見えるのですが、プログラム全体としてはあまり変化しません。 rdtsc 命令を使って実行時間を直接測定して見ると、実は movntpd 命令を使わないほうが 30% 程度短く、転送速度(上り下り合計) では 2.7GB/s 程度でていました。 (0.09words/clk 程度)

部分的にはキャッシュ内の移動ですんでいるはず、と思うとまだ遅いので、内側のループを 4 重にアンロールしてみます。

 void transpose_coltorow(int n, double a[][RDIM],int m, double at[][n],
                        int istart)
 {
     int i,j,k;
     double atmp[m][m];
     for(i=istart;i<n;i+=m){
        for(j=0;j<m;j++){
            double * atj = at[j]+i;
            for(k=0;k<m;k+=4){
                atmp[k][j]  =atj[k];
                atmp[k+1][j]  =atj[k+1];
                atmp[k+2][j]  =atj[k+2];
                atmp[k+3][j]  =atj[k+3];
            }
        }
        for(k=0;k<m;k++){
            double * aik = a[i+k];
            for(j=0;j<m;j+=4){
                aik[j] = atmp[k][j];
                aik[j+1] = atmp[k][j+1];
                aik[j+2] = atmp[k][j+2];
                aik[j+3] = atmp[k][j+3];
            }
        }
     }
 }

これで 0.115words/clk 程度まで。アンロール、と考えてみると、この関数は呼ぶ時の m の値はいつも同じなので、最内側は展開するべきでしょう。そうすると、

 void transpose_coltorow8(int n, double a[][RDIM], double at[][n],
                        int istart)
 {
     int i,j,k;
     const int m=8;
     double atmp[m][m];
     for(i=istart;i<n;i+=m){
        for(j=0;j<m;j++){
            double * atj = at[j]+i;
            atmp[0][j]  =atj[0];
            atmp[1][j]  =atj[1];
            atmp[2][j]  =atj[2];
            atmp[3][j]  =atj[3];
            atmp[4][j]  =atj[4];
            atmp[5][j]  =atj[5];
            atmp[6][j]  =atj[6];
            atmp[7][j]  =atj[7];
        }
        for(k=0;k<m;k++){
            v2df * atp = (v2df*) atmp[k];
            v2df * ap = (v2df*) a[i+k];
            *(ap)=*(atp);
            *(ap+1)=*(atp+1);
            *(ap+2)=*(atp+2);
            *(ap+3)=*(atp+3);
        }
     }
 }

とより簡潔で高速なコードになり、0.13word/clk、4.4GB/s となってまあよいかも、というところです。キャッシュにはいっているはずの割には遅いのが気になります。

次は行交換です。

 void swaprows(int n, double a[n][RDIM], int row1, int row2,
              int cstart, int cend)
 {
     /* WARNING: works only for row1 % 4 = 0 and RDIM >= n+4*/
     
     int j;
     if (row1 != row2){
        int jmax = (cend+1-cstart)/2;
        v2df *a1, *a2, tmp, tmp1;
        a1 = (v2df*)(a[row1]+cstart);
        a2 = (v2df*)(a[row2]+cstart);
        for(j=0;j<jmax;j+=2){
            tmp = a1[j];
            tmp1 = a1[j+1];
            a1[j]=a2[j];
            a1[j+1]=a2[j+1];
            a2[j]=tmp;
            a2[j+1]=tmp1;
            __builtin_prefetch(a1+j+16,1,0);
            __builtin_prefetch(a2+j+16,1,0);
        }
     }
 }

2重にアンロールし、 SSE を使い、プリフェッチもいれています。プリフェッチをいれると、大体 0.07words/clock、2語の上り下りの合計としては 4.7GB/s となって、まあよいところです。プリフェッチなしだと 0.55words/clock 程度ですが、それなりにプリフェッチの効果はあります。

swaprows の後で正規化をする scalerow もみておきます。

 void scalerow( int n, double a[n][RDIM], double scale,
                int row, int cstart, int cend)
 {
     int j;
     for(j=cstart;j<cend;j++) a[row][j]*= scale;
 }

こんなのですね。

いじった後は

 void scalerow( int n, double a[n][RDIM], double scale,
               int row, int cstart, int cend)
 {
     int j;
     int jmax = (cend+1-cstart)/2;
     v2df *a1 = (v2df*)(a[row]+cstart);
     v2df ss = (v2df){scale,scale};
     for(j=0;j<jmax;j+=2){
        __builtin_prefetch(a1+j+16,1,0);
        a1[j] *= ss;
        a1[j+1]*= ss;
     }
 }

こんな感じで、 0.16words/cycle、5.4GB/s です。これは、いじる前は 0.08words/cycle 程度だったので、SSE2 とプリフェッチの利用に非常に大きな効果があります。

但し、scale と swap を一体化すれば余計な主記憶アクセスを減らせるので、そっちも検討するべきですね。

GRAPE-DR のようなアクセラレータを使うシステムでは、Linpack Benchmark では行列乗算を速くするだけでは十分ではなく、主記憶全体をなめることになる、つまり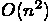のあらゆる操作について、主記憶の理論バンド幅に可能な限り近い速度がでる形にコードを書き直す必要があります。

ここまでで、行列乗算や3角行列の求解、つまり BLAS3 の用語でいうと DGEMM と DTRSM 以外についてはかなり高速なコードになっています。 DTRSM については DGEMM に変換し、変換できないところも再帰的に DGEMM を取り出すアクセラレータ専用のアルゴリズムを使うとして、 DGEMM 自体はどうか、というのが以下の表です。シングルコアの K8 アーキテクチャなので2演算/クロックが最大で、 K=64 だと十分な性能になっていますが K=8 ではかなり低いことがわかります。

    M     N   K             ops/clock
    2040    8   8           0.42988 
    2032   16  16           0.815346
    2024    8   8           0.435265
    2016   32  32           1.20451
    2008    8   8           0.428314
    2000   16  16           0.822711
    1992    8   8           0.434964
    1984 1985  64           1.70924

メモリバンド幅としてはどういうことになるかというと、 N=K=8 では 2 語読み出して1語格納するのに対して 16 演算ですから、 0.08語、1.35GB/s となって、同じようなアクセスである STREAM ADD の 4 割程度しかでていません。これはかなり大きな問題です。というのは、再帰的ブロッキングでは、各ブロックサイズでメモリアクセスは基本的には行列全体(細かいことをいうと 1/4)になり、階層のレベル数、つまり最大ブロックサイズの対数回全体をなめるからです。もちろん、ここで K が大きいところではアクセラレータを使うので、そっちのチューニングが問題ですが、 K が小さいところで主記憶のバンド幅がでていない、ということは、そこに大きなオーバーヘッドがある、ということになります。

今回 GotoBLAS 1.26 を使っていますが、中身をいじるのはやりたくないのでこのような小さい行列の時だけ書き下してみます。今までの例の中で同じようなアクセスパターンなのは行列転置ですが、この場合には単純に、転置しながら正方行列に書いて、それを連続アクセスでコピー、というのでよい性能がでました。従って、同じようなアプローチを考えてみます。

 void matmul_for_nk8(int n1, double a[][n1],
                         int n2, double b[][n2],
                         int n3, double c[][n3],
                         int m,
                         int n)
 {
     int i,j,k;
     const int kk = 8;
     const int kh = kk/2;
     int nh = n/2;
     v2df bcopy[nh][kk];
     v2df acopy2[kk][kk];
     for(k=0;k<kk;k++)
        for(j=0;j<nh;j++)
                bcopy[j][k] = *((v2df*)(b[k]+j+j));
     for(i=0;i<m;i+=kk){
        for(k=0;k<kk;k++){
            __builtin_prefetch(a+i+k+16,0,0);
            __builtin_prefetch(c+i+k+16,1,0);
        }
        for (j=0;j<n;j++){
            double * ap = (double*)( a[i+j]);
            for (k=0;k<kk;k++){
                acopy2[j][k]=(v2df){ap[k],ap[k]};
            }
        }
        for(k=0;k<kk;k++){
            v2df * cp = (v2df*) (c[i+k]);
            v2df * ap = acopy2[k];
            for(j=0;j<nh;j++){
                v2df * bp = bcopy[j];
                cp[j] -= ap[0]*bp[0] + ap[1]*bp[1]
                    + ap[2]*bp[2]    + ap[3]*bp[3]
                    + ap[4]*bp[4]    + ap[5]*bp[5]
                    + ap[6]*bp[6]    + ap[7]*bp[7];
            }
        }
     }
 }

これ、 N=K=8 でないと動かない代物ですが、

    M     N   K             ops/clock
    2040    8   8           0.727034
    2008    8   8           0.730609
    1992    8   8           0.782853

で、元々の BLAS に比べると 1.7 倍ほど速くなり、メモリバンド幅の7割程度は有効利用できていることがわかります。このコードでは、 b は転置しながらローカルにコピーします。a は、 SSE2 の2要素ベクトルに同じものがはいる形でふくらませたローカルコピーを作ります。これは、 SSE2 命令が無能でスカラとベクタの掛け算ができないことに対応するためです。 a は大きな行列で、b は小さいので、bを膨らませて a はそのまま、ですめば無駄が少ないのですが、行列の格納のしかたがそれはできないような順番になっています。

で、 a, c についてはプリフェッチをかけています。今回高速になっているのは主にこの効果ですね。実際の演算では、aの2要素(同じものがはいっている) とbの2要素をいっぺんに積算して、 c の2要素を求める、という形になっています。

a を膨らまさないで、SSE の2要素に同じ行のデータが入るようにして DOTD 命令で加算するほうが無駄が少なくて速いような気がしますが、 gcc 4.1.2 のイントリンシックには dotd はなさそうなので今回はそっちは使っていません。

ここは、さらにいじましい高速化を考えると、どうせ次に転置するんだから転置してから乗算するべきです。そうすると、もっと容易に高速化ができます。

転置したあとの行列乗算も、幅が狭いだけに性能が重要です。この場合、基本的にキャッシュに載っているはずなので、命令スケジューリングによるはずです。 GotoBLAS の性能は、 n=k=2、 4 で 0.4、 0.7 ops/clock となっていて、キャッシュだと思うとどうにも遅い、という感じです。メモリバンド幅としては3語で 4、 8 演算ですから、5GB/s 程度です。L2 でももっとでるはずなので、工夫の余地があります。

N=2048 の行列で、計算時間が大体 1.75 秒ですが、そのうち n=k=2 の行列の計算時間が 5ms 程度です。これは小さいように見えるのですが、大きな行列乗算が相対的に 100倍程度速くなると、行列サイズを10倍程度大きくしても無視できないわけです。

というわけで、ここまでで、

転置状態での細い行列乗算
3角行列の処理
swap/scale の一体化

以外は大体済んだ、ということになります。

Ci7 の機械を組んだので、そっちで実験(A64 と比較)をしています。

 Athlon, N=2K
 swaprows time=3.2801e+07
 scalerow time=1.42839e+07
 trans rtoc8 time=3.25526e+07
 trans ctor8 time=1.63445e+07
 Ci7 920 (3GHz), N=2K
 swaprows time=9.78e+06
 scalerow time=3.29607e+06
 trans rtoc8 time=1.42135e+07
 trans ctor8 time=6.05478e+06
 Ci7 920 (3GHz), N=8K
 swaprows time=1.79584e+08
 scalerow time=5.39146e+07
 trans rtoc8 time=2.53306e+08
 trans ctor8 time=1.1879e+08
 trans dgemm time=2.07928e+08
 trans nonrec cdec time=1.77051e+08

メモリアクセスの総量はそれぞれ 64MB, 32 MB, 32 MB, 32MB なので、速度は

             A64 2.1GHz   Ci7 3GHz  Ci7 (N=8K)

 swaprows      4.1            19.6    18.1
 scalerow      4.7            29.1    37.9
 trans rtoc8   2.07           6.7     8.1
 trans ctor8   4.1            15.9    17.2

です。32K の場合、このへんで2秒くらいはまだかかる計算になります。主記憶リミットであるので並列化には殆ど意味がないかな、という気もしますが、まあ、 OMP でやってみると:

  N=8K, Ci7
  trans rtoc8 time=1.74734e+08
  N=4k
  trans rtoc8 time=4.94381e+07
  N=2k
  trans rtoc8 time=1.77795e+07

意外に効果があります。N=2k では若干遅くなりますが、 8K では 1.5 倍近く速くなります。スレッドで書いたらもうちょっといいかもしれません。こういうものの並列化の場合、起動オーバーヘッドとメモリバンド幅の極限性能、キャッシュ効率の3つの要因があるので性能予測が困難ですが、今キャッシュのことは無視すると、N が無限に大きい時の性能は 8k の時から10-15% 程度の向上で、 11GB/s 程度と推測できます。 col2row については、

  N=8K trans ctor8 time=8.79587e+07
  N=4k trans ctor8 time=3.00645e+07

で、これもそれなりに効果があることがわかります。特に N がもっと大きいところを考えるので Open MP の起動オーバーヘッドは十分小さくなり、結構よくなることが期待できます。まあ、この場合、OpenMP の並列化ループは1000回くらいしか呼ばれていなくて、実行が 10マイクロ秒程度ですから OpenMP の起動オーバーヘッドはその程度あるわけです。ベクトル化に比べるとはるかにオーバーヘッドが大きく、利用が難しいもの、ということがわかります。

Ci7 (というか、Core 2 以降？)は、デフォルトでは勝手にに L2 に2ライン (128バイト)もってくる、というオプションがあるんだそうで、これは確かに Bios で有効になってたので、 1ライン単位での転置が遅いのはこれが原因と思われます。

とはいえ、このオプションを BIOS で切ると

 Nswap=0 cpsec =  46.3909 wsec=14.1913
 swaprows time=1.80358e+08
 scalerow time=5.39611e+07
 trans rtoc8 time=1.93491e+08
 trans ctor8 time=1.01146e+08
 trans dgemm time=2.42105e+08
 trans nonrec cdec time=1.65904e+08
 trans vvmul time=5.65689e+07
 trans findp time=1.06555e+08
 
 Nswap=0 cpsec =  46.4709 wsec=13.9176
 swaprows time=1.81601e+08
 scalerow time=5.47325e+07
 trans rtoc8 time=1.86051e+08
 trans ctor8 time=8.86901e+07
 trans dgemm time=2.48892e+08
 trans nonrec cdec time=1.66319e+08
 trans vvmul time=5.68656e+07
 trans findp time=1.06808e+08

ON にすると

 Nswap=0 cpsec =  46.4349 wsec=46.4116
 swaprows time=1.79092e+08
 scalerow time=5.39498e+07
 trans rtoc8 time=1.90267e+08
 trans ctor8 time=1.01477e+08
 trans dgemm time=2.3238e+08
 trans nonrec cdec time=1.66845e+08
 trans vvmul time=5.69506e+07
 trans findp time=1.07196e+08

Nswap=0 cpsec = 46.7269 wsec=13.9467 swaprows time=1.80993e+08 scalerow time=5.44132e+07 trans rtoc8 time=1.88233e+08 trans ctor8 time=9.26843e+07 trans dgemm time=2.40648e+08 trans nonrec cdec time=1.65907e+08 trans vvmul time=5.64983e+07 trans findp time=1.06597e+08

全然変わらない。これは、プリフェッチが十分効いてない、ということだと思われ、、、というか、コードをちゃんとみたら、あ、プリフェッチの入れかたが間違ってました、、、まあ、でも、直しても普通は変わらないと、、、Core i7 のメモリレイテンシは 200サイクル程度らしいので、20GB/s = 7B/cycle とすれば大雑把には 200語程度先読みをしていないといけないことになります。。

以下は細かい作業記録なのであんまり読んでも役に立たないです。

 Nswap=0 cpsec =  46.4469 wsec=14.2066
 swaprows time=1.82082e+08
 scalerow time=5.46414e+07
 trans rtoc8 time=1.89987e+08
 trans ctor8 time=9.16793e+07
 trans dgemm time=2.45399e+08
 trans nonrec cdec time=1.68357e+08
 trans vvmul time=5.64953e+07
 trans findp time=1.08689e+08
 solve tri u time=9.15278e+07
 solve tri   time=1.05368e+09
 matmul nk8  time=2.3478e+08
 matmul snk  time=3.00549e+08

nk8 は、256 MB アクセスのはず。snk も同じ。

16で転置すると

 Nswap=0 cpsec =  46.5109 wsec=13.6755
 swaprows time=1.80648e+08
 scalerow time=5.29178e+07
 trans rtoc8 time=0
 trans ctor8 time=9.17586e+07
 trans dgemm time=3.54391e+08
 trans nonrec cdec time=1.66416e+08
 trans vvmul time=5.67401e+07
 trans findp time=1.07049e+08
 solve tri u time=9.06005e+07
 solve tri   time=9.15348e+08
 matmul nk8  time=0
 matmul snk  time=2.97462e+08

転置のメモリアクセス: 512MB。これを 0.028 秒だと、16GB/s で結構速い。

matmul snk は 256MB を 0.1 秒で遅い。演算速度は 8k x 8k /4 * 32 =0.54e9 くらいなので、 5Gflops

 OMP_NUM_THREADS=2, snk を OMP で。 
  
 Emax=  4.007e-10
 Nswap=0 cpsec =  46.0989 wsec=23.3147
 swaprows time=1.80596e+08
 scalerow time=5.2993e+07
 trans rtoc8 time=0
 trans ctor8 time=8.32039e+07
 trans dgemm time=1.84467e+19
 trans nonrec cdec time=1.66061e+08
 trans vvmul time=5.74618e+07
 trans findp time=1.06753e+08
 solve tri u time=9.12501e+07
 solve tri   time=1.06944e+09
 matmul nk8  time=0
 matmul snk  time=1.55114e+08

なんだか素晴らしい効果がある。

m=8 で転置に戻すと

 Emax=  8.745e-10
 Nswap=0 cpsec =  46.1349 wsec=23.2356
 swaprows time=1.79216e+08
 scalerow time=5.33178e+07
 trans rtoc8 time=1.6885e+08
 trans ctor8 time=8.19126e+07
 trans dgemm time=1.95553e+08
 trans nonrec cdec time=1.66091e+08
 trans vvmul time=5.65165e+07
 trans findp time=1.06811e+08
 solve tri u time=1.84467e+19
 solve tri   time=1.07682e+09
 matmul nk8  time=1.27066e+08
 matmul snk  time=1.52946e+08

Nthreads=1, N=16384

 Emax=  1.076e-06
 Nswap=0 cpsec =  417.914 wsec=160.704
 swaprows time=7.40931e+08 ops/cycle=0.181147
 scalerow time=3.47836e+08 ops/cycle=0.385864
 trans rtoc8 time=1.84467e+19 ops/cycle=7.27596e-12
 trans ctor8 time=1.84467e+19 ops/cycle=7.27596e-12
 trans mmul  time=1.35821e+09 ops/cycle=1.48229
 trans nonrec cdec time=1.84467e+19 ops/cycle=7.27596e-12
 trans vvmul time=2.23035e+08 ops/cycle=0.60178
 trans findp time=1.84467e+19 ops/cycle=7.27596e-12
 solve tri u time=1.81516e+08 ops/cycle=9.02621e-05
 solve tri   time=1.84467e+19 ops/cycle=8.88178e-16
 matmul nk8  time=0 ops/cycle=inf
 matmul snk  time=1.19488e+09 ops/cycle=1.79724
 trans mmul8 time=7.07553e+08 ops/cycle=1.51754
 trans mmul4 time=4.08479e+08 ops/cycle=1.31432
 
 Nt=4
 Nswap=0 cpsec =  420.382 wsec=118.056
 swaprows time=1.84467e+19 ops/cycle=7.27596e-12
 scalerow time=3.48263e+08 ops/cycle=0.385392
 trans rtoc8 time=6.80027e+08 ops/cycle=0.197371
 trans ctor8 time=3.0702e+08 ops/cycle=0.437162
 trans mmul  time=1.37626e+09 ops/cycle=1.46285
 trans nonrec cdec time=6.41575e+08 ops/cycle=0.2092
 trans vvmul time=2.21756e+08 ops/cycle=0.605251
 trans findp time=4.15484e+08 ops/cycle=0.323039
 solve tri u time=1.81714e+08 ops/cycle=9.01635e-05
 solve tri   time=5.17148e+09 ops/cycle=3.16814e-06
 matmul nk8  time=0 ops/cycle=inf
 matmul snk  time=6.14184e+08 ops/cycle=3.49649
 trans mmul8 time=7.25474e+08 ops/cycle=1.48006
 trans mmul4 time=4.0895e+08 ops/cycle=1.3128

Nt=2, N=16384, NB=2048 相当いじったあと

 Emax=  1.471e-07
 Nswap=0 cpsec =  440.624 wsec=222.468
 swaprows time=8.39751e+08 ops/cycle=0.15983
 scalerow time=4.17531e+08 ops/cycle=0.321456
 trans rtoc8 time=1.02016e+09 ops/cycle=0.131565
 trans ctor8 time=5.5054e+08 ops/cycle=0.243793
 trans mmul  time=1.35954e+09 ops/cycle=1.48085
 trans nonrec cdec time=6.41812e+08 ops/cycle=0.209123
 trans vvmul time=2.22362e+08 ops/cycle=0.603601
 trans findp time=4.15344e+08 ops/cycle=0.323148
 solve tri u time=1.41841e+10 ops/cycle=1.1551e-06
 solve tri   time=8.92199e+10 ops/cycle=1.83636e-07
 matmul nk8  time=0 ops/cycle=inf
 matmul snk  time=1.19747e+09 ops/cycle=1.79335
 trans mmul8 time=7.08126e+08 ops/cycle=1.51631
 trans mmul4 time=4.09517e+08 ops/cycle=1.31099
 DGEMM       time=4.85794e+11 ops/cycle=6.03555

再帰的な DTRSM は実装した。

GotoBLAS 2 1.01 に変更

 Enter n, seed, nb:N=20480 Seed=1 NB=512
 read/set mat end
 copy mat end
 Emax=  3.087e-07
 Nswap=0 cpsec =  585.725 wsec=146.726
 swaprows time=1.1845e+09 ops/cycle=0.17705
 scalerow time=6.05163e+08 ops/cycle=0.346543
 trans rtoc8 time=1.3443e+09 ops/cycle=0.156003
 trans ctor8 time=8.0741e+08 ops/cycle=0.259738
 trans mmul  time=2.41859e+09 ops/cycle=1.30065
 trans nonrec cdec time=1.02126e+09 ops/cycle=0.205349
 trans vvmul time=3.63753e+08 ops/cycle=0.576532
 trans findp time=6.51132e+08 ops/cycle=0.322078
 solve tri u time=7.77699e+08 ops/cycle=2.63341e-05
 solve tri   time=1.6045e+10 ops/cycle=1.27641e-06
 matmul nk8  time=0 ops/cycle=inf
 matmul snk  time=1.94126e+09 ops/cycle=1.72849
 trans mmul8 time=0 ops/cycle=inf
 trans mmul4 time=6.3223e+08 ops/cycle=1.32683
 DGEMM       time=3.67084e+11 ops/cycle=15.6003

Enter n, seed, nb:N=16384 Seed=1 NB=2048

 read/set mat end
 copy mat end
 Emax=  3.090e-08
 Nswap=0 cpsec =  329.265 wsec=82.7602
 swaprows time=8.37005e+08 ops/cycle=0.160355
 scalerow time=4.17547e+08 ops/cycle=0.321443
 trans rtoc8 time=7.71399e+08 ops/cycle=0.173993
 trans ctor8 time=5.27207e+08 ops/cycle=0.254582
 trans mmul  time=1.59757e+09 ops/cycle=1.2602
 trans nonrec cdec time=6.5203e+08 ops/cycle=0.205846
 trans vvmul time=2.29239e+08 ops/cycle=0.585492
 trans findp time=4.16039e+08 ops/cycle=0.322609
 solve tri u time=5.49025e+09 ops/cycle=2.9842e-06
 solve tri   time=3.42907e+10 ops/cycle=4.77797e-07
 matmul nk8  time=0 ops/cycle=inf
 matmul snk  time=1.23869e+09 ops/cycle=1.73368
 trans mmul8 time=0 ops/cycle=inf
 trans mmul4 time=4.10097e+08 ops/cycle=1.30913
 DGEMM       time=1.76038e+11 ops/cycle=16.6556

swaprows and scalerow OMP化

 <cfcafs03:/home/makino/src/linsol>
 Enter n, seed, nb:N=16384 Seed=1 NB=128
 read/set mat end
 copy mat end
 Emax=  4.767e-09
 Nswap=0 cpsec =  306.351 wsec=76.7172
 swaprows time=8.07664e+08 ops/cycle=0.16618
 scalerow time=3.58689e+08 ops/cycle=0.37419
 trans rtoc8 time=7.92825e+08 ops/cycle=0.16929
 trans ctor8 time=5.24754e+08 ops/cycle=0.255773
 trans mmul  time=1.59751e+09 ops/cycle=1.26025
 trans nonrec cdec time=6.50838e+08 ops/cycle=0.206223
 trans vvmul time=2.30045e+08 ops/cycle=0.583441
 trans findp time=4.15841e+08 ops/cycle=0.322762
 solve tri u time=1.21474e+08 ops/cycle=0.000134877
 solve tri   time=3.71787e+09 ops/cycle=4.40683e-06
 matmul nk8  time=0 ops/cycle=inf
 matmul snk  time=1.25042e+09 ops/cycle=1.71741
 trans mmul8 time=0 ops/cycle=inf
 trans mmul4 time=4.09244e+08 ops/cycle=1.31186
 DGEMM       time=1.95923e+11 ops/cycle=14.9652

Core i7 に最適化された GotoBLAS は結構速いので、色々普通にやってあまり問題ない。

 Enter n, seed, nb:N=20480 Seed=1 NB=2048
 read/set mat end
 copy mat end
 Emax=  6.227e-08
 Nswap=0 cpsec =  623.027 wsec=156.475
 swaprows time=1.34135e+09 ops/cycle=0.156346
 scalerow time=6.46645e+08 ops/cycle=0.324313
 trans rtoc8 time=1.26259e+09 ops/cycle=0.1661
 trans ctor8 time=7.75399e+08 ops/cycle=0.270461
 trans mmul  time=2.43097e+09 ops/cycle=1.29402
 trans nonrec cdec time=9.99599e+08 ops/cycle=0.209799
 trans vvmul time=3.49642e+08 ops/cycle=0.5998
 trans findp time=6.44818e+08 ops/cycle=0.325232
 solve tri u time=6.86921e+09 ops/cycle=2.98142e-06
 solve tri   time=5.42023e+10 ops/cycle=3.77844e-07
 matmul nk8  time=0 ops/cycle=inf
 matmul snk  time=2.04036e+09 ops/cycle=1.64453
 trans mmul8 time=0 ops/cycle=inf
 trans mmul4 time=6.36945e+08 ops/cycle=1.31701
 DGEMM       time=3.48804e+11 ops/cycle=16.4179

20k の時:

 swap 0.5sec
 scale 0.24sec
 trans (r->c) 0.47sec
 trans (c->r) 0.29sec
 large DGEMM  131.2 sec

DGEMM の時間の測定のしかたが間違っていたので修正。 cblas_dgemm を全部合計にする。

 Enter n, seed, nb:N=16384 Seed=1 NB=256
 read/set mat end
 copy mat end
 Emax=  3.875e-09
 Nswap=0 cpsec =  300.335 wsec=75.2046
 swaprows time=8.10285e+08 ops/cycle=0.165643
 scalerow time=3.71966e+08 ops/cycle=0.360833
 trans rtoc8 time=7.6822e+08 ops/cycle=0.174713
 trans ctor8 time=5.02146e+08 ops/cycle=0.267288
 trans mmul  time=1.56957e+09 ops/cycle=1.28269
 trans nonrec cdec time=6.43971e+08 ops/cycle=0.208422
 trans vvmul time=2.26705e+08 ops/cycle=0.592036
 trans findp time=4.13498e+08 ops/cycle=0.324591
 solve tri u time=2.58505e+08 ops/cycle=6.33798e-05
 solve tri   time=5.89804e+09 ops/cycle=2.77787e-06
 matmul nk8  time=0 ops/cycle=inf
 matmul snk  time=1.24804e+09 ops/cycle=1.72069
 trans mmul8 time=0 ops/cycle=inf
 trans mmul4 time=4.10276e+08 ops/cycle=1.30856
 DGEMM       time=1.89628e+11 ops/cycle=15.462

DGEMM の分が71.2 秒なのでそれ以外が4秒

 swap 0.3sec
 scale 0.15sec
 trans (r->c) 0.3sec
 trans (c->r) 0.2sec
 mmul in trans 0.6sec
 nb=2          0.3sec
 small mmul r  0.5sec

 
 Enter n, seed, nb:N=20480 Seed=1 NB=256
 read/set mat end
 copy mat end
 Emax=  1.686e-07
 Nswap=0 cpsec =  582.388 wsec=145.805
 swaprows time=1.25323e+09 ops/cycle=0.167339
 scalerow time=5.8671e+08 ops/cycle=0.357443
 trans rtoc8 time=1.2708e+09 ops/cycle=0.165026
 trans ctor8 time=7.75856e+08 ops/cycle=0.270302
 trans mmul  time=2.42934e+09 ops/cycle=1.29489
 trans nonrec cdec time=1.00069e+09 ops/cycle=0.20957
 trans vvmul time=3.49502e+08 ops/cycle=0.60004
 trans findp time=6.44612e+08 ops/cycle=0.325335
 solve tri u time=3.28611e+08 ops/cycle=6.23229e-05
 solve tri   time=9.28552e+09 ops/cycle=2.20559e-06
 matmul nk8  time=0 ops/cycle=inf
 matmul snk  time=2.02897e+09 ops/cycle=1.65377
 trans mmul8 time=0 ops/cycle=inf
 trans mmul4 time=6.36088e+08 ops/cycle=1.31878
 DGEMM       time=3.71893e+11 ops/cycle=15.3986

TIMETEST を外しても合計時間は殆ど (0.1秒も)変わらない。

まだ間違っていたのでもう一度修正。

 Enter n, seed, nb:N=16384 Seed=1 NB=256
 read/set mat end
 copy mat end
 Emax=  3.875e-09
 Nswap=0 cpsec =  300.427 wsec=75.2283
 swaprows time=8.10422e+08 ops/cycle=0.165615
 scalerow time=3.75172e+08 ops/cycle=0.35775
 trans rtoc8 time=7.66713e+08 ops/cycle=0.175056
 trans ctor8 time=5.03349e+08 ops/cycle=0.266649
 trans mmul  time=1.57006e+09 ops/cycle=1.28229
 trans nonrec cdec time=6.97766e+08 ops/cycle=0.192354
 trans vvmul time=2.26423e+08 ops/cycle=0.592773
 trans findp time=4.67333e+08 ops/cycle=0.287199
 solve tri u time=2.66089e+08 ops/cycle=6.15733e-05
 solve tri   time=5.89679e+09 ops/cycle=2.77846e-06
 matmul nk8  time=0 ops/cycle=inf
 matmul snk  time=1.24246e+09 ops/cycle=1.72842
 trans mmul8 time=0 ops/cycle=inf
 trans mmul4 time=4.10345e+08 ops/cycle=1.30834
 DGEMM       time=1.93737e+11 ops/cycle=15.1341

DGEMM 72.6 sec.

残りは 2.5 sec なので、説明はできている。

 Enter n, seed, nb:N=32768 Seed=1 NB=2048
 a, awork offset size= 7f223c800000 7f243d000000 200800000 200800000 200800000
 size of size_t and off_t long= 8 8 8
 read/set mat end
 copy mat end
 Emax=  4.229e-07
 Nswap=0 cpsec =  2441.84 wsec=612.648
 swaprows time=3.30799e+09 ops/cycle=0.162295
 scalerow time=1.60583e+09 ops/cycle=0.334325
 trans rtoc8 time=4.15807e+09 ops/cycle=0.129115
 trans ctor8 time=2.23611e+09 ops/cycle=0.240091
 trans mmul  time=6.2654e+09 ops/cycle=1.28532
 trans nonrec cdec time=2.62081e+09 ops/cycle=0.204849
 trans vvmul time=9.41764e+08 ops/cycle=0.57007
 trans findp time=1.66965e+09 ops/cycle=0.321548
 solve tri u time=1.10225e+10 ops/cycle=2.97282e-06
 solve tri   time=1.42092e+11 ops/cycle=2.30611e-07
 matmul nk8  time=0 ops/cycle=inf
 matmul snk  time=5.46641e+09 ops/cycle=1.5714
 trans mmul8 time=0 ops/cycle=inf
 trans mmul4 time=1.62096e+09 ops/cycle=1.32482
 DGEMM       time=1.60535e+12 ops/cycle=14.6113

DGEMM 603.4 sec 残り 9 sec

34 K なら 10秒ちょっと。

34K の時のパネル分解の計算量。 N, K で考える。行列要素数は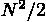で、要素当りの計算量は基本的に内積演算の平均の長さが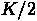なので、

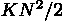
42.56Gflops で 29 秒。

 Enter n, seed, nb:N=34816 Seed=1 NB=2048
 a, awork offset size= 7fb84f200000 7fba91a00000 242800000 242800000 242800000
 size of size_t and off_t long= 8 8 8
 read/set mat end
 copy mat end
 Emax=  5.044e-07
 Nswap=0 cpsec =  2912.46 wsec=730.613
 swaprows time=3.72683e+09 ops/cycle=0.162625
 scalerow time=1.96941e+09 ops/cycle=0.307745
 trans rtoc8 time=4.34275e+09 ops/cycle=0.139561
 trans ctor8 time=2.38512e+09 ops/cycle=0.254108
 trans mmul  time=6.94446e+09 ops/cycle=1.30912
 trans nonrec cdec time=2.903e+09 ops/cycle=0.208776
 trans vvmul time=1.02328e+09 ops/cycle=0.592288
 trans findp time=1.86832e+09 ops/cycle=0.324396
 solve tri u time=1.16829e+10 ops/cycle=2.98007e-06
 solve tri   time=1.60738e+11 ops/cycle=2.16601e-07
 matmul nk8  time=0 ops/cycle=inf
 matmul snk  time=6.39244e+09 ops/cycle=1.51698
 trans mmul8 time=0 ops/cycle=inf
 trans mmul4 time=1.82715e+09 ops/cycle=1.32683
 DGEMM       time=1.91709e+12 ops/cycle=14.6758

どれだけ短くできるか、を考える。

   計算量の半分: K=1024  600Gflops 14倍
   計算量の 1/4 : K=512  300       7
   計算量の 1/8 : K=256  150       3.5
   計算量の 1/16 : K=128 75        1.75

 合計は: 0.21 
 
 Enter n, seed, nb:N=34816 Seed=1 NB=2048
 a, awork offset size= 7fae21c00000 7fb064400000 242800000 242800000 242800000
 size of size_t and off_t long= 8 8 8
 read/set mat end
 copy mat end
 Emax=  5.044e-07
 Nswap=0 cpsec =  2910.57 wsec=730.139
 swaprows time=3.72784e+09 ops/cycle=0.162581
 scalerow time=1.79725e+09 ops/cycle=0.337224
 trans rtoc8 time=4.34249e+09 ops/cycle=0.139569
 trans ctor8 time=2.40224e+09 ops/cycle=0.252296
 trans mmul  time=5.83755e+09 ops/cycle=1.55736
 trans nonrec cdec time=2.9062e+09 ops/cycle=0.208546
 trans vvmul time=1.02325e+09 ops/cycle=0.592304
 trans findp time=1.86805e+09 ops/cycle=0.324444
 solve tri u time=1.16613e+10 ops/cycle=2.9856e-06
 solve tri   time=1.6063e+11 ops/cycle=2.16747e-07
 matmul nk8  time=0 ops/cycle=inf
 matmul snk  time=6.36856e+09 ops/cycle=1.52267
 trans mmul8 time=0 ops/cycle=inf
 trans mmul4 time=1.82159e+09 ops/cycle=1.33087
 DGEMM       time=1.91704e+12 ops/cycle=14.6762

NB=256 では

 Enter n, seed, nb:N=34816 Seed=1 NB=256
 a, awork offset size= 7fad35600000 7faf77e00000 242800000 242800000 242800000
 size of size_t and off_t long= 8 8 8
 read/set mat end
 copy mat end
 Emax=  9.244e-08
 Nswap=0 cpsec =  2797.93 wsec=700.362
 swaprows time=3.57559e+09 ops/cycle=0.169504
 scalerow time=1.71234e+09 ops/cycle=0.353947
 trans rtoc8 time=4.35866e+09 ops/cycle=0.139051
 trans ctor8 time=2.40053e+09 ops/cycle=0.252476
 trans mmul  time=5.83701e+09 ops/cycle=1.5575
 trans nonrec cdec time=2.90349e+09 ops/cycle=0.208741
 trans vvmul time=1.02339e+09 ops/cycle=0.592227
 trans findp time=1.8687e+09 ops/cycle=0.324331
 solve tri u time=5.74246e+08 ops/cycle=6.06291e-05
 solve tri   time=2.66881e+10 ops/cycle=1.30455e-06
 matmul nk8  time=0 ops/cycle=inf
 matmul snk  time=6.3678e+09 ops/cycle=1.52286
 trans mmul8 time=0 ops/cycle=inf
 trans mmul4 time=1.8209e+09 ops/cycle=1.33138
 DGEMM       time=1.83881e+12 ops/cycle=15.3006
 
 swaprows time=3.57559e+09 ops/cycle=0.169504
 scalerow time=1.71234e+09 ops/cycle=0.353947
 trans rtoc8 time=4.35866e+09 ops/cycle=0.139051
 trans ctor8 time=2.40053e+09 ops/cycle=0.252476
 trans mmul  time=5.83701e+09 ops/cycle=1.5575
 trans nonrec cdec time=2.90349e+09 ops/cycle=0.208741
 trans vvmul time=1.02339e+09 ops/cycle=0.592227
 trans findp time=1.8687e+09 ops/cycle=0.324331
 matmul snk  time=6.3678e+09 ops/cycle=1.52286
 trans mmul4 time=1.8209e+09 ops/cycle=1.33138

このへんの細かいところを全部もうちょっとつめたい、というのが残ったチューニングになる。

行列データ: 9.7GB (not GiB)。交換は read+write 18GB, scale 9.7GB、 trans rtoc, ctor それぞれ 9.7GB

trans mmul: K=16 の下。演算数としては、要素当り16演算なので、9.7G 演算、時間2秒なので 4Gflops 程度しかでていない。メモリアクセスは、 K= 2, 4, 8 で3回、それぞれ行の下半分を半分読んで半分書く。なので、 15GB。2秒なので、 7.5GB/s。ここはもうちょっと速くならないか、という気がする。そもそも、データサイズとして 34k の場合でも16行、4MB なので、 L3 キャッシュに全部はいっているんだと思うんだが、、、

あと、見た目でできそうなチューニング箇所は以下の通り。

現状の転置方式は、行列消去が進んでも n x 16 の配列にコピーする、という形、つまり、上のほうに空きがある形にコピーするようになっている。これはコードが簡単だが、明らかに効率は悪い。配列のディメンションを変えて、 (n-i) x 16 の領域を連続アクセスできるようにすればいくらかは速くなるはず。

あと、転置前の nx16 の行列乗算がちょっとありえないほど遅い。 32k で、転置とこの乗算で合わせて4秒程度かかっていて、時間の大半である。ここでは、実は乗算の結果を一旦メモリにストアしてから転置しているが、これは本当は無駄なので、乗算した結果を転置しながら直接ストアすればここのメモリアクセスを 60% にできるだけでなく、不連続ストアを減らすこともできる。

が、それ以前にここまでを GotoBLASにすると、

 Enter n, seed, nb:N=8192 Seed=1 NB=128
 read/set mat end
 copy mat end
 Emax=  6.833e-10
 Nswap=0 cpsec =  39.4825 wsec=9.88793 37.0658 Gflops
 swaprows time=2.04298e+08 ops/cycle=0.164242
 scalerow time=7.06527e+07 ops/cycle=0.474921
 trans rtoc8 time=1.43615e+08 ops/cycle=0.233642
 trans ctor8 time=1.37003e+08 ops/cycle=0.244917
 trans mmul  time=2.94734e+08 ops/cycle=1.7077
 trans nonrec cdec time=1.69648e+08 ops/cycle=0.197789
 trans vvmul time=5.64071e+07 ops/cycle=0.594862
 trans findp time=1.13391e+08 ops/cycle=0.295919
 solve tri u time=5.94506e+07 ops/cycle=0.000137795
 solve tri   time=9.13853e+08 ops/cycle=9.39969
 matmul nk8  time=0 ops/cycle=inf
 matmul snk  time=54240 ops/cycle=9898.06
 trans mmul8 time=0 ops/cycle=inf
 trans mmul4 time=8.26731e+07 ops/cycle=1.62348
 trans mmul2 time=4.56105e+07 ops/cycle=1.47135
 DGEMM       time=2.50872e+10 ops/cycle=14.9516

変更前:

 N=8192 Seed=1 NB=128
 Emax=  1.902e-09
 Nswap=0 cpsec =  39.7945 wsec=9.97176 36.7542 Gflops
 swaprows time=2.03733e+08 ops/cycle=0.164698
 scalerow time=7.06972e+07 ops/cycle=0.474622
 trans rtoc8 time=1.4062e+08 ops/cycle=0.238617
 trans ctor8 time=1.36213e+08 ops/cycle=0.246337
 trans mmul  time=2.95006e+08 ops/cycle=1.70612
 trans nonrec cdec time=1.6697e+08 ops/cycle=0.20096
 trans vvmul time=5.64536e+07 ops/cycle=0.594372
 trans findp time=1.10669e+08 ops/cycle=0.303197
 solve tri u time=5.95494e+07 ops/cycle=0.000137566
 solve tri   time=9.09796e+08 ops/cycle=9.44161
 matmul nk8  time=0 ops/cycle=inf
 matmul snk  time=3.05898e+08 ops/cycle=1.75506
 trans mmul8 time=0 ops/cycle=inf
 trans mmul4 time=8.29545e+07 ops/cycle=1.61797
 trans mmul2 time=4.55855e+07 ops/cycle=1.47215
 DGEMM       time=2.50133e+10 ops/cycle=14.9958

元々は nx16 に3.05898e+08 サイクル。DGEMM の差はずっと小さいので、これはこっちを使えばOKと思われる。

 DGEMM       time=2.50872e+10 ops/cycle=14.9516
 DGEMM       time=2.50133e+10 ops/cycle=14.9958

 HPL の速度は

 ============================================================================
 T/V                N    NB     P     Q               Time             Gflops
 ----------------------------------------------------------------------------
 WR00L2C2        4096   128     1     1               1.36          3.362e+01
 WR00L2C4        4096   128     1     1               1.35          3.401e+01
 WR00L2C2        8192   128     1     1              10.18          3.601e+01
 WR00L2C4        8192   128     1     1              10.10          3.631e+01
 ============================================================================

なので、 N=8192 の場合に、計算量が 1.5% 程度増加している(dtrsm の処理のため)が時間は 2% 程度減少していることがわかる。

ToC