5. プログラムを楽に書く。(2009/6/13)
プログラムをどういうふうに書くのが楽か、というのは、ある程度楽に書いて
いる人にとってはそうでない人にわかるように説明するのは非常に難しいこと
である。というのは、「楽でない書き方」は極めて不自然かつ奇妙なものに
見えるので、思い付くことも真似をすることも難しいからである。
これは、例えば
Cプログラミング診断室 といった、そのような実例を集めて、何が問題かを解説している本
を読んで見るのが、楽な書き方がどんなものか既にわかっている人にも、そう
でなく、この本にあるような書き方をしている人にも有益であると思う。
ネット上ではこの本については評価が分裂している。悪い評価は、
SMBH
IMBH
普通の星
というところである。
で、重力を計算するのに本当に質点でやると、粒子がたまたま近づいた時に計
算が発散する。それを防ぐために、重力ポテンシャルエネルギーを
のどちらかであろう。以下、某君が書いていたプログラムを例に、同じような
ことを考えてみる。もう5年くらい前なので時効であろう。今はもうこんなプ
ログラムは書かない立派な研究者になっているし。
#include <stdio.h>
#include <math.h>
#include "bh.h"
/* ----------------------------------- */
void get_force_host(int ni, int nj,
double *m, double (*x1)[3], double (*v1)[3],
double (*xi)[3], double (*vi)[3],
double (*ai)[3], double (*ji)[3],
double *eps2i, int *indexi, double *pi)
{
int ii, j, k, idi;
double rinv, r2, r2inv, r3inv, r5inv;
double xdotv, xdotvr5inv,r3invdx;
double r3invdvetc;
double dx[3], dv[3];
for(ii=0;ii<ni;ii++){
for (k = 0; k < 3; k++) {
ai[ii][k] = 0.0;
ji[ii][k] = 0.0;
}
pi[ii] = 0.0;
}
// ALL <== FS
for(ii=0;ii<ni;ii++){
idi = indexi[ii];
for(j=0;j<nj;j++){
if(idi!=j){
r2 = eps2i[ii];
xdotv = 0.0;
for (k = 0; k < 3; k++) {
dx[k] = x1[j][k] - xi[ii][k] ;
dv[k] = v1[j][k] - vi[ii][k] ;
r2 += dx[k] * dx[k];
xdotv += dx[k] * dv[k];
}
r2inv = 1.0 / r2 ;
rinv = sqrt(r2inv);
r3inv = rinv * r2inv;
r5inv = r3inv * r2inv;
xdotvr5inv = 3.0 * xdotv * r5inv;
for (k = 0; k < 3; k++) {
r3invdx = r3inv * dx[k];
r3invdvetc = r3inv * dv[k] - xdotvr5inv * dx[k];
if(r3invdx == 0.0) fprintf(stderr,"idi=%d ii=%d j=%d ",idi,ii,j);
if(r3invdvetc == 0.0) fprintf(stderr,"idi=%d ii=%d j=%d ",idi,ii,j);
ai[ii][k] += m[j] * r3invdx;
ji[ii][k] += m[j] * r3invdvetc;
}
pi[ii] -= m[j] * rinv;
}
}
}
}
void get_force_from_bh(int ni, int nj,
double *m,
double (*x1)[3], double (*v1)[3],
double (*xi)[3], double (*vi)[3],
double (*ai)[3], double (*ji)[3],
double *eps2, int *indexi,double *pi,
int BHnum, int *BHi, double eps_bb2)
{
int ii, j, k,idi;
double rinv, r2, r2inv, r3inv, r5inv;
double xdotv, xdotvr5inv,r3invdx;
double r3invdvetc;
double dx[3], dv[3];
for(ii=0;ii<ni;ii++){
idi = indexi[ii];
// --- ALL <== BH ---
for (j = nj; j < (nj+BHnum) ; j++) {
if(idi!=j){
if(idi < nj ) r2 = eps2[j];
if(idi >= nj ) r2 = eps_bb2;
xdotv = 0.0;
for (k = 0; k < 3; k++) {
dx[k] = x1[j][k] - xi[ii][k] ;
dv[k] = v1[j][k] - vi[ii][k] ;
r2 += dx[k] * dx[k];
xdotv += dx[k] * dv[k];
}
r2inv = 1.0 / r2 ;
rinv = sqrt(r2inv);
r3inv = rinv * r2inv;
r5inv = r3inv * r2inv;
xdotvr5inv = 3.0 * xdotv * r5inv;
for (k = 0; k < 3; k++) {
r3invdx = r3inv * dx[k];
r3invdvetc = r3inv * dv[k] - xdotvr5inv * dx[k];
if(r3invdx == 0.0) fprintf(stderr,"idi=%d ii=%d j=%d ",idi,ii,j);
if(r3invdvetc == 0.0) fprintf(stderr,"idi=%d ii=%d j=%d ",idi,ii,j);
ai[ii][k] += m[j] * r3invdx;
ji[ii][k] += m[j] * r3invdvetc;
}
pi[ii] -= m[j] * rinv;
}
}
}
}
/* ---------------------------------------------- */
/* --------------------------------------------- */
void get_force_initial(int n, double *eps2, double *m,
double (*x0)[3], double (*v0)[3],
double (*a0)[3], double (*j0)[3], double *p,
int BHnum, int *BHi, double eps_bb2)
{
int i, j, k, b;
double rinv, r2, r2inv, r3inv, r5inv;
double xdotvr5inv,r3invdx, r3invdvetc;
double xdotv, dx[3], dv[3];
for (i = 0; i < n; i++) {
for (k = 0; k < 3; k++) {
a0[i][k] = 0.0;
j0[i][k] = 0.0;
}
p[i] = 0.0;
}
/* --- FS <== FS --- */
for (i = 0; i < (n -BHnum); i++) {
for (j = i+1; j < (n-BHnum); j++) {
r2 = eps2[i];
xdotv = 0.0;
for (k = 0; k < 3; k++) {
dx[k] = x0[j][k] - x0[i][k] ;
dv[k] = v0[j][k] - v0[i][k] ;
r2 += dx[k] * dx[k];
xdotv += dx[k] * dv[k];
}
r2inv = 1.0 / r2 ;
rinv = sqrt(r2inv);
r3inv = rinv * r2inv;
r5inv = r3inv * r2inv;
xdotvr5inv = 3.0 * xdotv * r5inv;
for (k = 0; k < 3; k++) {
r3invdx = r3inv * dx[k];
r3invdvetc = r3inv * dv[k] - xdotvr5inv * dx[k];
a0[i][k] += m[j] * r3invdx;
a0[j][k] -= m[i] * r3invdx;
j0[i][k] += m[j] * r3invdvetc;
j0[j][k] += - m[i] * r3invdvetc;
}
p[i] -= m[j] * rinv;
p[j] -= m[i] * rinv;
}
}
/* --- FS <==> BH --- */
for (b = 0; b < BHnum ; b++) {
j = BHi[b];
for (i = 0; i < (n-BHnum) ; i++) {
r2 = eps2[j];
xdotv = 0.0;
for (k = 0; k < 3; k++) {
dx[k] = x0[j][k] - x0[i][k] ;
dv[k] = v0[j][k] - v0[i][k] ;
r2 += dx[k] * dx[k];
xdotv += dx[k] * dv[k];
}
r2inv = 1.0 / r2 ;
rinv = sqrt(r2inv);
r3inv = rinv * r2inv;
r5inv = r3inv * r2inv;
xdotvr5inv = 3.0 * xdotv * r5inv;
for (k = 0; k < 3; k++) {
r3invdx = r3inv * dx[k];
r3invdvetc = r3inv * dv[k] - xdotvr5inv * dx[k];
a0[i][k] += m[j] * r3invdx;
a0[j][k] -= m[i] * r3invdx;
j0[i][k] += m[j] * r3invdvetc;
j0[j][k] += - m[i] * r3invdvetc;
}
p[i] -= m[j] * rinv;
p[j] -= m[i] * rinv;
}
}
/* --- B1 <=> B2 --- */
if(BHnum !=0 ){
for (i = n-BHnum ; i < n; i++) {
for (j = i+1; j < n; j++) {
r2 = eps_bb2;
xdotv = 0.0;
for (k = 0; k < 3; k++) {
dx[k] = x0[j][k] - x0[i][k] ;
dv[k] = v0[j][k] - v0[i][k] ;
r2 += dx[k] * dx[k];
xdotv += dx[k] * dv[k];
}
r2inv = 1.0 / r2 ;
rinv = sqrt(r2inv);
r3inv = rinv * r2inv;
r5inv = r3inv * r2inv;
xdotvr5inv = 3.0 * xdotv * r5inv;
for (k = 0; k < 3; k++) {
r3invdx = r3inv * dx[k];
r3invdvetc = r3inv * dv[k] - xdotvr5inv * dx[k];
a0[i][k] += m[j] * r3invdx;
a0[j][k] -= m[i] * r3invdx;
j0[i][k] += m[j] * r3invdvetc;
j0[j][k] += - m[i] * r3invdvetc;
}
p[i] -= m[j] * rinv;
p[j] -= m[i] * rinv;
}
}
}
}
これは、直接重力計算(全ての粒子からの力を本当に計算する) のN体プログラ
ムで、粒子に非常に重いブラックホール(といっても相対論的効果を考えるわ
けではなくて単に重いニュートン力学、ニュートン重力の質点)と、それ以外
の普通の粒子(星)がある場合を扱おうというものである。で、物理モデルとして
は非常に重い銀河中心にあるブラックホール(SMBH, supermassive black
hole)、もうちょっと軽い「中間質量ブ
ラックホール」(IMBH, intermediate-mass black hole)、それから普通の星、
というものを扱いたいものである。 それぞれの質量は
 太陽質量
太陽質量
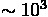 太陽質量
太陽質量
 太陽質量
太陽質量

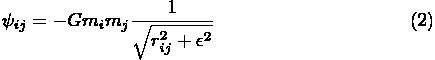
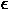 にどの程度の大きさを取るべきかはここでは議論しないが、
ブラックホールの影響を考える場合には、これらについてはこれらの回りの星
の軌道が大きく変わってしまうような値にしてはいけない。
ちなみに、 この
にどの程度の大きさを取るべきかはここでは議論しないが、
ブラックホールの影響を考える場合には、これらについてはこれらの回りの星
の軌道が大きく変わってしまうような値にしてはいけない。
ちなみに、 この  のことを通常ソフトニング長という。面
倒なので単にソフトニングということも多い。
のことを通常ソフトニング長という。面
倒なので単にソフトニングということも多い。