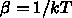9. 最適化(1)
この章と次では最適化の話をする。
これは天文学の観測・理論のあらゆる場面で必要になる
とても重要な技術である。
現代の天文学の観測においては、例えばなにかを観測してデータをとったとし
て、それから実際に天文学的に意味があることをいうまでにはいろいろなステッ
プがはいるのが普通である。多くの場合に、これはいろいろな自由パラメータ
があるモデルを持ってきて、そのモデルのパラメータを観測データを「もっと
もうまく説明する」ように決めるということである。例えば銀河内のガスの速
度から質量分布を推測するとか、銀河団ガスからのX線放射から質量を推定す
るといった場合には、結局そういうことをやっているわけである。もっともう
まく説明するとは、具体的にはなんらかの形で誤差を表現して、
それを最小化するということである。
これは、形式的には例えばこういうふうな話になる:
「ある領域
つまり、最適化というのは要するにこういう話である。
とはいえ、実際にどうやって上の問題の答を求めるかというのは、もちろん領
域
これに対して、同じような多次元空間内の最適化でも、もとの関数がどんなも
のか良くわからないとか、計算が面倒であるとかいうと、急に話がややこしく
なる。
例えば、図 13 は連星重力レンズと推定されたものの観測結果と、それのモデルである。
横軸は時間、縦軸は明るさである。連星レンズの特徴は、単一星の場合と違っ
てピークが2つできることと、そのピークが単一星のばあいよりもずっと明る
いことである。
連星レンズの場合、パラメータの数は非常に多い。連星自体の軌道要素が 6
個、その他に質量比、周期、光源の速度、それぞれの我々からの距離というこ
とで10個以上ある。なお、このうちいくつかは縮退しているので、本当のパラ
メータは9個である。で、どのパラメータを変えるとなにがどう変わるかとい
うのは簡単にはわからない。こういう時に、どうやってレンズのライトカーブ
の観測から、物理的な意味を引き出せるのだろうか?
というわけで、世の中には多様な最適化手法がある。これらを簡単にまとめる
のが今日の話ということになる。
ここでは、本来分類されるべきものは手法ではなく、問題の分類があってそれ
に対応して手法があるのかもしれないが、まあ、実際には、問題の定義自体が、
「こういう方法で解ける」というのをかっこよくいっただけというところもあ
る。とりあえず、ここで考える分類は以下のようなものということにしておく。
適当にやるよりも、真面目にやったほうがいいに決まってるのではないかと思
うかも知れないが、必ずしもそういう問題ばかりではない。例えば、ある種の
問題では、まともにやって正しい答を求めるのに必要な手間が、問題の大きさ
の多項式よりも速く増大する。
この一例が巡回セールスマン問題というものである。これは、名前の由来は、
「あるセールスマンが一日に沢山のお客を回る時に、どの順番で回るのがもっと
も効率的か?」ということであるが、例えば電話線やネットワークの線をどう
引くのか効率的かといった問題にも応用される、実用上はいろんなところで出
てくる問題である。
素朴な解法は、全部の順序を調べてもっとも短いのを捜すというものだが、こ
れは手間が回る場所の数
ところが、このような問題に対して「シミュレーテッドアニーリング」や「遺
伝的アルゴリズム」といった、確率的な方法を使うと、それが本当にもっとも
良い解であるという保証はないが、まあまあそんなには悪くない解が
まあ、この辺の詳しい話は来週にして、決定論的方法のほうの分類だが、連続
関数というのは定義域が
この講義では、離散的な場合の決定論的方法はやらない。これは、問題によっ
てあまりに沢山いろんな方法があるので、何をやるべきか良くわからないから
である。
ここで述べる手法は、とりえあえず定義域があまり変な形をしていなくて(と
いうのをちゃんと定義することはできるが、やると話が長くなるので省略)、
関数はその定義域のなかで連続で極小値を1つだけ持つという場合のためのも
のである。
この場合、目的関数
微分を数値的にやればいいのではとも考えられるが、これも丸め誤差等の影響
があって難しい場合が多い。
もっとも、微分を数値的にやるのではなく、数式的にやる、つまり、もとの関
数の数式から数式処理プログラムに生成させたり、あるいはプログラム自体を
「微分」する、つまり、目的関数を計算するプログラムから微分を計算するプ
ログラムを自動生成するといった研究もかなり進んではいる。実際に問題を解
こうという時には、こういった手法が使えないかどうかも考えてはみるべきで
あろう。
というわけで、以下はニュートン法とかではない方法。まず1変数、それから
多変数にいく。
まあ、1変数ならニュートン法でいいのではないかとも思うわけだが、多変数
の場合のための準備ということで一応説明しておく。実際には、多変数の問題
を解く時に形式的には1変数の問題の繰り返しになって、そこでは簡単には2階
微分が計算できなくてニュートン法というわけにはいかないので、それ以外の
方法がいるわけである。
良く本に載っているのは、黄金分割法というものである。これは、以下のよう
な方法である。区間
一度ですむのはいいが、収束は遅い。一度反復した時に区間の幅が 0.62倍
にしかならないからである。これはつまり一次収束で、反復毎に定数分の1に
なるものである。
もうちょっと賢い方法としては、疑似ニュートン法的なものがある。要するに
3点あれば2次関数で近似できるので、その極値を求めようというものである。
最適化問題ではない非線形方程式では Secant 法と呼ばれているものの拡張で
ある。 Secant 法程速くはないが、 一次よりも速い収束をすることが知られ
ている。
多変数の場合にも、黄金分割にあたるような直接探索法というのはあることは
あるが、あんまり使えないので省く。大抵の本で最初に出ているのは最急降下
法というものである。とりあえず、関数
最急降下法のよいところは、いつかは収束することであり、よくないところは
収束が必ずしも速くないことである。これは、2変数で目的関数が2次形式の場
合についていろいろ実験したり考えてみたりすればわかるが、結局直交する2
方向の繰り返しに陥ってしまうからである。この事情は多変数の場合でも同じ
で、結局2方向になっていくということが証明されている。
というわけで、速く答を出そうとするなら、やはり疑似ニュートン法的なもの
を考えたくなる。1変数の時のように簡単に2次形式の近似式が構成できるわけ
ではないが、その辺をなんとかうまくやろうというわけでいろんな方法が提案
されている。
多分良くつかわれているのは DFP(Davidon-Fletcher-Powell)法や
BFGS(Broyden-Fletcher-Goldfarb-Shanno)法で、どちらも考案者の名前である。
時々 Variable Metric method(可変計量法) と呼ばれることもある。
以下、基本的な考え方を説明する。
目的関数が、以下の2次形式
ニュートン法では、
目的関数が上の2次形式なら、これはもちろん
そういうわけで、考え方としては、ヘッシアンなり
ここで、ちょっと定義を続ける。まず、共役という概念を定義する。2つのベ
クトル
さらに、互いに共役な
これは、
ここでの実際的な問題は、互いに共役な
このように
まあ、自分でプログラムを書くならこれをつかうので OK であろう。ライブラ
リとかだと BFGS のほうが少しよいようである。
さて、さっき共役な
共役な
というベクトル列を考える。ここで
である。
なお、疑似ニュートン法、CG法のどちらの場合でも、方向は決まるが1次元問
題を繰り返し毎に解く必要はある。これは黄金分割なり疑似ニュートン法なり
を使うことになる。多次元の反復では勾配を求めないといけないので少なくと
も
CG 法は現在最適化よりも大規模な線型方程式を解くのに広く使われている。
今、
何故こんなややこしいことをするのかと思うかもしれない。理由はちゃんとあっ
て、一つはこの方法は反復法であるにもかかわらず原理的には有限回で収束す
ること、つまり、ガウスザイデルや SOR とは違って、(計算精度が無限に高い
なら)収束が保証されていることである。もう一つはいろいろ工夫することで
収束を非常に速くできることが多いということである。
収束を速くするための工夫は色々な「前処理」と言われるもので、それだけを扱った本
がいっぱいあるのでここではこれ以上は扱わない。
大抵の問題では、目的関数の定義域が実数全体ということはない。例えば、銀
河の回転曲線から質量分布を求めようというときには、質量はどこでも正でな
ければならない。
このような制約にはいろんな場合があるが、制約が等式の場合はラグランジュ
の未定乗数法が使えるのでこれは省略する。不等式の場合は話が難しくなる。
問題によっては厳密にできる場合もあるが、ここではペナルティ法というもの
を紹介しておく。これは、
この方法では、制約条件のところに解があるとそれに境界の外側から近付く。
このために外点法と呼ばれる。内点法というのもあって、これは
プログラムが必要なものはプログラムを提出すること。
1変数関数
上の関数について、3点を使う疑似ニュートン法のプログラムを作り、
収束が一次より速いことを確認せよ。
2変数の2次形式
9.1. 概要
 上で定義された実数値関数
上で定義された実数値関数  がある。その最小値とそれ
を与える
がある。その最小値とそれ
を与える 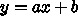 を求めよ」
を求めよ」
 がどんなものかと関数
がどんなものかと関数  がどんなものかによる。例えば、観測デー
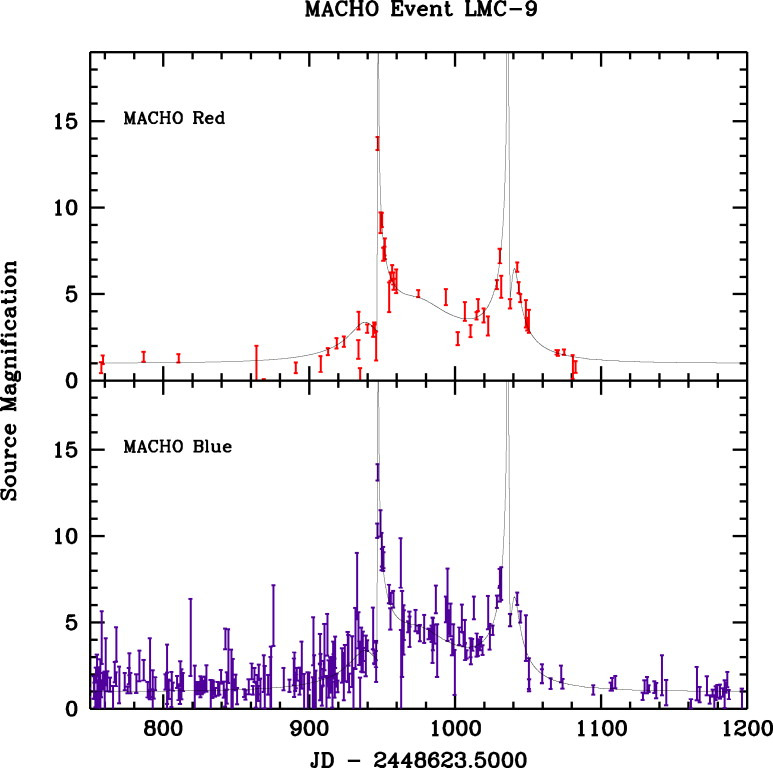
タを線形回帰して直線近似するなら、
がどんなものかによる。例えば、観測デー
タを線形回帰して直線近似するなら、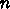 は直線
は直線 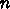 の係数
の係数 の
集合ということになろう。
の
集合ということになろう。 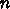 は2乗残差である。これは2次形式の最小化に
なり、微分すれば連立一次方程式が出てきて解ける。パラメータの数が多くて
も、2次形式なら話は同じである。
は2乗残差である。これは2次形式の最小化に
なり、微分すれば連立一次方程式が出てきて解ける。パラメータの数が多くて
も、2次形式なら話は同じである。
9.2. 最適化手法の分類
決定論的方法とは、文字通り問題とやり方を決めればあとは機械的に計算が進
んで、いつでも同じ答がでるものである。これに対して、確率的方法とは、良
さそうな答を捜す時に乱数等を使ってある意味「適当」にやるものである。
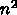 の階乗で増えるので
の階乗で増えるので  が 10を超える当たりか
ら実際的ではなくなる。が、例えば
が 10を超える当たりか
ら実際的ではなくなる。が、例えば といった、
といった、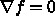 の冪乗の手間で正し
い解が見つかるような方法は知られていない。
の冪乗の手間で正し
い解が見つかるような方法は知られていない。
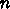 程度の手間で求まる。
程度の手間で求まる。
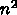 次元ユークリッド空間の連続な部分集合で、最適
化したい目的関数も連続な実数値関数であるようなものである。そうでないも
のというのは要するにそれ以外の全部である。上の巡回セールスマン問題は後
者の一例である。
次元ユークリッド空間の連続な部分集合で、最適
化したい目的関数も連続な実数値関数であるようなものである。そうでないも
のというのは要するにそれ以外の全部である。上の巡回セールスマン問題は後
者の一例である。
9.3. 連続関数の最適化
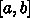 が2階微分を持てば、原理的には話は極めて簡単になっ
て、
が2階微分を持てば、原理的には話は極めて簡単になっ
て、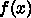 という方程式をニュートン法で解けばいい。が、多くの場
合にこれはあんまりうまくいかない。というのは、変数の数
という方程式をニュートン法で解けばいい。が、多くの場
合にこれはあんまりうまくいかない。というのは、変数の数  が多くなる
と計算しないといけない2階微分の数は
が多くなる
と計算しないといけない2階微分の数は 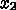 に比例して増えるわけで、計算
量が増えるだけでなく書かないといけないプログラムの量が増えるという問題
があるからである。
に比例して増えるわけで、計算
量が増えるだけでなく書かないといけないプログラムの量が増えるという問題
があるからである。
9.3.1. 1変数の場合
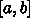 のなかに関数
のなかに関数 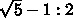 の最小値があることはわかっ
ているとする。
の最小値があることはわかっ
ているとする。
なお、一般には別に黄金分割でなくても、区間内に適当に2点とってその大き
い方を新しい区間の端にするというので構わない。黄金分割のミソは上の説明
の「細かいこと」、つまり、分割点の一方を使い回せるので反復一度について
関数計算が1度ですむということである。
 ,
, 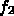 を、
を、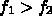 をそれぞれ
をそれぞれ  およびその逆に
内分する点とする。
およびその逆に
内分する点とする。
 ,
, 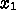 を計算する。
を計算する。
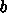 なら最小値は
なら最小値は  にあるので、
にあるので、 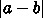 を
を 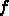 で置
き換え、1に戻る。細かいことをいえば <$x_2$> が 次の <$x_1$> になるので、使
い回せる。
で置
き換え、1に戻る。細かいことをいえば <$x_2$> が 次の <$x_1$> になるので、使
い回せる。
 を
を 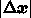 で置き換え、同様に 1に戻る。
で置き換え、同様に 1に戻る。
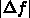 が十分小さくなるまで繰り返す。
が十分小さくなるまで繰り返す。
9.3.2. 多変数の場合
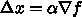 が
が 次元ユークリッド空間全体で定
義されているとする。この方法の原理は、「ちょっと動いた時にもっとも関数
値が減る方向に動く」というのを繰り返すことである。もっとも減る方向は、
次元ユークリッド空間全体で定
義されているとする。この方法の原理は、「ちょっと動いた時にもっとも関数
値が減る方向に動く」というのを繰り返すことである。もっとも減る方向は、

 が一定の時に
が一定の時に を最大にすればよく、もちろん
を最大にすればよく、もちろん 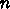 、つまり一階
導関数自体が方向ということになる。 これで、あとは前節で述べた適当な方
法を使ってその方向での1次元最適化を適当にやり、あとはまたそこで新しく
勾配を求めて同じことを繰り返す。
、つまり一階
導関数自体が方向ということになる。 これで、あとは前節で述べた適当な方
法を使ってその方向での1次元最適化を適当にやり、あとはまたそこで新しく
勾配を求めて同じことを繰り返す。

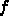 は
は  次元実ベクトル、
次元実ベクトル、 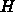 は
は  次元正方行列で、
対称にとって良いので正定値である。
次元正方行列で、
対称にとって良いので正定値である。
 を2次形式で近似してそれの極値を求める。形式的に
は、近似値
を2次形式で近似してそれの極値を求める。形式的に
は、近似値 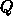 の回りでのテイラー展開
の回りでのテイラー展開

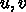 はヘッシアンで、2階偏導関数を要素
とする正方行列である。つまり
はヘッシアンで、2階偏導関数を要素
とする正方行列である。つまり

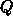 として、
として、

 で、正しい答が求まる。
で、正しい答が求まる。
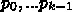 の近似値を作ってい
こうというのが基本になる。
の近似値を作ってい
こうというのが基本になる。
 が
が 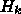 について共役であるとは
について共役であるとは

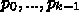 個のベクトル
個のベクトル 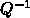 を考え
を考え 、これら
に対して、
、これら
に対して、

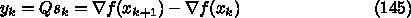
 が
が  が張る部分空間では
が張る部分空間では  みた
いなものであるということを意味している。したがって、
みた
いなものであるということを意味している。したがって、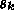 を順番に発生
させる方法がなにかあれば、それを使って、
を順番に発生
させる方法がなにかあれば、それを使って、

 を計算していけばよい。
を計算していけばよい。
 を作るよい方法があるかどうかよく
わからないことである。一つの考え方は、反復による修正量
を作るよい方法があるかどうかよく
わからないことである。一つの考え方は、反復による修正量 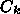 を使うことである。
を使うことである。 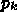 は共役ではないが、それでもなんと
か
は共役ではないが、それでもなんと
か

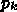 という項を追加することにすると、 これの満たす
べき式は
という項を追加することにすると、 これの満たす
べき式は

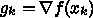 は
は

 をとる一つの方法(DFP法)は、
をとる一つの方法(DFP法)は、

9.3.3. CG法
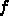 を作る方法はよくわからないと書いたが、これは
原理的には知られている。但し、いつでも上手くいくわけではないのでそれを
使わない方法も研究されているわけである。
を作る方法はよくわからないと書いたが、これは
原理的には知られている。但し、いつでも上手くいくわけではないのでそれを
使わない方法も研究されているわけである。
 を直接作る方法が共役勾配法、すなわち
CG(Conjugate gradient)法である。これは形式的には簡単である。いま、
を直接作る方法が共役勾配法、すなわち
CG(Conjugate gradient)法である。これは形式的には簡単である。いま、
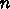 と書くことにして、
:eqnarray]
p_0 &=& -g_0\\
p_k &=& -g_k + \beta_kp_{k-1}\quad (k=1,2, ...)
と書くことにして、
:eqnarray]
p_0 &=& -g_0\\
p_k &=& -g_k + \beta_kp_{k-1}\quad (k=1,2, ...)
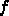 は
は

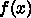 が2次関数の時には、これで求まる
が2次関数の時には、これで求まる 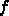 は互いに共役であることを証明
できる。さらに、ちょっと変形すると、
は互いに共役であることを証明
できる。さらに、ちょっと変形すると、
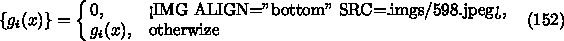
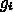 個の関数を計算することになるが、1次元問題では反復毎に1度
個の関数を計算することになるが、1次元問題では反復毎に1度  を計
算するだけなのでここではそれほど効率に気を使う必要はないことに注意。
を計
算するだけなのでここではそれほど効率に気を使う必要はないことに注意。
9.3.4. CG 法の応用:連立1次方程式
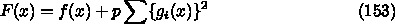
9.4. 制約つき最適化

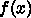 を最小化せよという問題を、
を最小化せよという問題を、 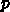 と
と  を適
当に組み合わせて作った関数を制約なしで最小化せよという問題に置き換える。
具体的には、
を適
当に組み合わせて作った関数を制約なしで最小化せよという問題に置き換える。
具体的には、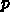 を、
を、


 の値を適当に大きくして
いって、こちらの条件に見合う解になったら止める。
の値を適当に大きくして
いって、こちらの条件に見合う解になったら止める。
 を
を

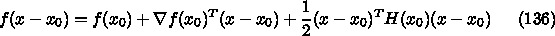 を小さくするにしたがって領域の内側から真の解に近付く。
を小さくするにしたがって領域の内側から真の解に近付く。
9.5. 練習
9.5.1. 練習 1

 での最小値を黄金分割法で求めるプログラムを作り、答を求
めよ。
での最小値を黄金分割法で求めるプログラムを作り、答を求
めよ。
9.5.2. 練習 2
9.5.3. 練習 3