3. C++言語入門 III
プログラムを書いて実行しても、でるものが数字ばかりではつまらない。せっかく再帰
をやったので、再帰を使ってわりあい簡単なプログラムで複雑な図形を書いてみよう。
再帰を使うことで、角度、長さを変えて自分自身を呼び出すという形で簡潔に
アルゴリズムが表現できている。
まず、このプログラムのコンパイルには
インストールは C ラ イブラリのインストールページから、Ubuntu なら
gr-latest-Ubuntu-x86_64.tar.gz
を落としてきて、それを
どこか適当なディレクトリで tar xzf とかで展開する。そうすると、grという
てディレクトリと、その下に libとか include とかのサブディレクトリができる。そのディレクトリの名前
を GRDIR に設定して。bashなら
3.1. お絵書き
1:// tree.cpp
2:#define _USE_MATH_DEFINES
3:#include <iostream>
4:#include <cmath>
5:#include <gr.h>
6:using namespace std;
7:
8:void draw(double x1, double y1, double x2, double y2)
9:{
10: double xa[] = {x1,x2};
11: double ya[] = {y1,y2};
12: gr_polyline(2,xa,ya);
13:}
14:
15:void tree(int n, double x, double y, double angle, double length)
16:{
17: double x1, y1;
18: if (n >0){
19: x1 = x + length*cos(angle);
20: y1 = y - length*sin(angle);
21: draw(x,y,x1,y1);
22: tree(n-1,x1,y1,angle + 0.25, length*0.7);
23: tree(n-1,x1,y1,angle - 0.25, length*0.7);
24: }
25:}
26:
27:int main()
28:{
29: int n;
30: cerr << "Level of the tree? :";
31: cin >> n;
32: gr_setwindow(0,1,0,1);
33: tree(n, 0.5, 0.0, -M_PI/2, 0.25);
34: cerr <<"Enter some char + retern to finish:";
35: char c; cin >>c;
36:}
これは、樹形図を書くプログラムである。原理は、指定した長さと角度で一本
線を引き、その先から角度をつけて2本線を引き、それぞれの端からまた角度
をつけて、、、というのを繰り返すだけである。
3.2. コンパイル・実行の方法
がインストールされている必要がある。
export GRDIR=/foo/var/gr
csh 系なら
setenv GRDIR /foo/var/gr
でよい(/foo/bar は実際のディレクトリの名前に置き換えること)。あとは
export GKS_WSTYPE=x11
を実行してから、
Getting Startedにあるような作業をすればよい。
g++ tree.cpp -o tree -std=c++11 -I $GRDIR/include -L $GRDIR/lib -Wl,-rpath,$GRDIR/lib -lGR
でコンパイルし、
./tree
で実行できるはずである。上手くいけば図 2 のような絵
がでてくるはずである。なお、環境変数 GKS_WSTYPE を x11 にしないと何も
でないかもしれない。

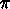 のような数学でよく使われる定数を使えるようにする。その上の
のような数学でよく使われる定数を使えるようにする。その上の
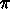 の値が
必要なところで使うことができる。
の値が
必要なところで使うことができる。