9. ケプラー問題とコマンドラインオプション
赤木 :ここまででわりと色々やったことになるわけで、
学生C:ケプラー問題ってなんでしょう?
赤木 :太陽の周りを惑星が1個だけ回ってる、というやつ。
学生C:これでも解析解あるんですよね?
赤木 :そうだけど、惑星2つになると解析解があるとはいいがたくなるのね。
で、惑星の軌道とか、太陽系が将来どうなるかとかは、ニュートン以降今でも
研究対象なの。コンピュータが使えるようになってからは、ここでやってる
ような数値計算が研究の大事な方法になっていて、もう30年くらい前だけど、
1980年代に数値計算で冥王星の軌道はカオス的だと示されたとか、色々あるのよ。
学生C:カオス的ってなんですか?
赤木 :それはまたそれだけで1冊本を読まないといけないような話なので今日
は詳しくはしないけど、大雑把には、すごく近い2つの軌道、つまり、
太陽系が2つあって、ほとんど同じ初期条件から出版したとして、2つの間の
差が指数関数的にどんどん成長するかどうかで定義されてるわね。
学生C:はあ。
赤木 :まあ、まずはケプラー問題やってみましょう。前回書いた
色々な積分公式を使い回せるようにして、 require して使えるようにして、
それでケプラー問題解いてみて。運動方程式はわかるわね?重力定数
学生C: grlib.cr みたいに module とかにするんでしょうか?
赤木 : そのほうがあとで変なことがおきないわね。そうしましょう。
学生C:そうしたら、 integratorlib.cr という名前で
赤木 :私もよく知らないので解説お願い。
学生C:4行目はこういう module 作りますです。module の名前は大文字で始
まらないといけないらしいので、そうしてます。
赤木 :次の extend self ってなに?
学生C:私もあんまりわかってないんですが、これがないと
Integrators.leapfrog みたいな形でモジュールで定義した関数を
呼ぶのができないみたいです。それでも include Integrators とすれば
leapfrog で呼べるということらしいです。
赤木 :何故それが extend self なのかわからないけど、やりたいことはわかったわ。
学生C:その後はずっと関数の定義で、これはモジュールにする前と同じです。
1箇所だけ違うのは、 45-46 行で、これjは4次シンプレクティック公式で
使う d1, d2 ですが、モジュールの定数として、関数の外で定義してます。
Crystal では大文字で始まるものは定数とのことでした。定数なので多分
コンパイルの時か、あるいはプログラムの実行の最初とかで1度だけ評価され
てくれるのではないかと、、、
赤木 :なるほど。ケプラー問題解くプログラムのほうは?
学生C:作ってみました。
学生C:はい。最初の5行はいいですね?r equire と include だけなので。
6-11行がケプラー問題の運動方程式というか加速度項を計算する関数です。基
本的に x は前に定義した Vector3型を想定してますが、別に2次元ベクトルで
も内積とスカラーとの掛け算があるクラスならこの関数で計算できます。計算
している式は運動方程式
赤木 :16行は mを1にして、17行は前の調和振動子の時と同じで関数を関数に
渡せるようにしてるのね。
えーと、その次の18から24行目はなにこれ?
学生C:すみません、ちょっと変わったことしてみたくて。やってるのは、
integrator に、その上の ff と同じように時間積分公式のほうをいれるので
すが、ARGV[3]、つまりコマンドラインで与える4個目のパラメータでその値を
変えるので if ...else ... end になってます。if文は真になるほうの
中身の最後の式が値になるそうなので、こんなふうに画面に文字とか書いてか
ら式書いたらその最後の式が値になって integrator に入るわけです。
赤木 :ちょっと気持ち悪いけど、これでコンパイルも実行もできたのね?
学生C:はい。どんどんいくと、 26-30行は前にオイラー法で軌道書いたプロ
グラムと同じで、周期あたりのステップとか何周期かとか、グラフの軸の範囲
とかです。
31、32は初期条件の設定ですね。ここで初めてが Vector3 ということになり
ます。33-37はグラフの枠とかラベルで、前と同じです。
38-39は、積分精度がよくわからなかったので、エネルギーを計算するように
して初期のエネルギーをだしてあと最大誤差を初期化してます。
40-46行が実際の時間積分で、ほぼ integrator を call するだけですね。
あとは前の x の座標から線ひいて、初期からのエネルギーの変化を更新して、
というくらいです。
赤木 :なるほどね、積分公式を選択する if文がこっちにはないから、わかり
やすいといえばわかりやすいわね。
プログラムって、 while とか if とかが何重にも重なる(ネストする、という
のね)と、それだけで何やってるかわからなくなるので、なるべくそうならな
いほうがいいの。
と、うんちくはいいとして結果は?
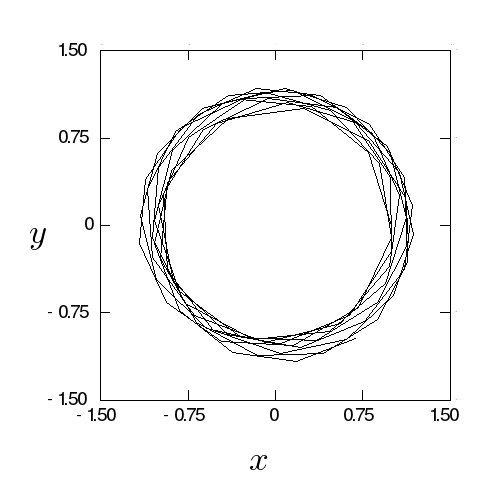
学生C:1周期30ステップ、10周期、リープフロッグでだしたのが
図 14 です。ケプラー問題でも、
リープフロッグでは誤差が一方的にたまったりしないことがわかります。
エネルギー誤差は 2.5% とでてました。
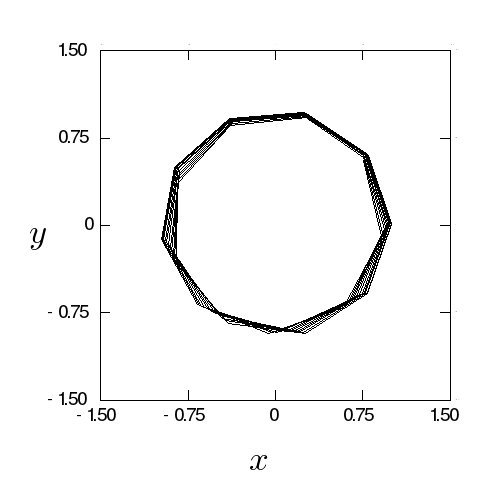
学生C:4次シンプレクティックだと
図 15 です。エネルギー誤差は 0.9% で、すごくよ
くなってはいないですがだいぶよいです。ちなみに、100ステップにすると
リープフロッグで 3.9e-6、
4次シンプレクティックでは 2.6e-10 となって、なんか精度よすぎるんです
が、、、リープフロッグでは2桁のはずなのが4桁、4次シンプレクティックで
も4桁のはずが7桁近くあがってます。
赤木 :ああ、これはそうなるのよ。円軌道だけ特別なの。これ昔から知られて
いると思うんだけどちゃんと解説してあるのはあんまりみたことない気がする
わ。楕円軌道もできるようにしてみて。最後のコマンドラインパラメータに離
心率追加して、遠点から計算始めてみて。
学生C:軌道長半径は1のままとすると、遠点では太陽からの距離は 1+e とい
うことですね。速度は距離に直交して、エネルギーは -0.5 なので、速度を v
として
学生C:えーと、、離心率とステップでループ回すようにプログラム変えますか?
赤木 :それでもいいんだけど、今まであんまりこういう話をしてないけど、1
つのパラメータを入力して積分するプログラムと、ループ回すのと、時間積分
するところは同じなのに違うものができるのはあんまりよくないじゃない。
学生C:そうしたらどうするのがいいですかね?
赤木 :UNIX 風の考え方だと、個々のプログラムはなるべく機能が少ないもの
とか単一機能にして、それを組合せて、みたいな感じね。
学生C:でも今のプログラム画面にグラフとかでますし、、、
赤木 :じゃあまずはその辺まで実行時に設定できるようにしておいて。
学生C:そうすると5個コマンドラインオプションつけるわけですね。自分でも
どれがなにか段々わからなくなってきてて、、、
赤木 :そうねえ、、、ちゃんとドキュメント書くとか、ヘルプメッセージを
だすようにするとかかしら。
学生C:ヘルプメッセージってどうやってだすんですか?
赤木 :Cとかの普通のプログラムだと、単にプログラムの中でそのままとかだけど、、、
学生C:あと、例えば、コマンド実行の時に -n 10 とするとステップ数の変数
に10いれるとかはうまい関数とかあるのでしょうか?
赤木 :うーん、うまいかどうか難しいけど、作者氏が作ったの使ってみる?
学生C:もっと普通ののほうがよくないですか?
赤木 :まあそうかもだけど、わりと便利よ。一応こっちは Crystal のパッケー
ジ管理ツールでいれられるから、Crystal のプログラムのソースファイルがあ
るディレクトリに、 shard.yml っていうファイル作って、中身を
学生C:えーと、すみません、github ってなんですか?
赤木 :あ、、知らないか。そうよね。これは、git っていうソフトウェアのバージョン管理
ツールがあって、それを使って複数の人が共同開発するようなプロジェクト用
に、その git のサーバーを立ててるサイトなの。お金払うと非公開のプロジェ
クト、ただでも公開のプロジェクトはつくれるから、ソフトウェアを公開する
には便利なの。あ、最近はただでも非公開のもつくれたかも。
要するに、そこにソフトウェアあげておくと、他の人がコマンド1つでダウン
ロードとか、最新版への更新とかができるわけ。バージョン管理というのは、
データベースにして、昔の状態も残してある、ということね。だから、
なんかの理由で古いのを使いたいとか、間違ってバグありのをいれちゃったと
かにも対応できると。あと、他の人がこう修正したらと提案するとか
こういう問題があったというとかもやりやすくて記録が残るしかけがあるの。
学生C:それって、すごいソフトウェア書けるプロな人が使うもんじゃないですか?
赤木 :あ、そうでもないわ。あなたが色々プログラムが書く時にも、あと卒
業論文とかも、バージョン管理して、そのデータベースを自分の手元の機械の
ほかにあちこちに置くのは絶対しないといけないことよ。
まあ学生で1-2年の間だと運がよければあんまり困ったことにならないかもし
れないけど、特に卒業論文書いているとそのデータがあるノートPCとかが壊れ
る、ということは結構あるから。
あと、1箇所だと日本だと地震とか津波で計算機ごとデータが消えるとかだっ
て絶対におこらないとはいえないわ。そうじゃなくても、計算機が壊れること
はあるし。私は基本的に全部の文章とかプログラムとかを、
学生C:それちょっと神経質すぎるというか、パラノイアックじゃないですか?
赤木 :まあ年とるとその間には色々あるのよ。これはこれで重要なんだけど
ちょっと脱線したわね。そういうわけで shards install してみて。
学生C: はあ。 shards install でリターン、と。
赤木 :そしたら、 lib/clop/src の下に clop.cr と clopsample.cr ができ
てるはずね。サンプルのほう実行してみて。
学生C:
赤木 : あとヘルプで -h でなんかでると書いてあるわね。それつけてみて。
あ、クリスタルコンパイラのオプションと区別しないといけないから、 -- を
最初につけてね。
学生C:
赤木 : 見方はなんとなくわかるかしら? 1文字の短いオプションと、それを同じことになる長いオプションがあって、データ型(あれば)とデフォルトの値と説明がちょっとでるのね。
学生C:はい。 -n になんか値いれたらどうなるんでしょうか?
赤木 :まあやってみれば。
学生C:
赤木 :そうね。この clop ライブラリ、クラスを普通に定義
するんじゃなくて、テキストで
学生C:どうやってるんですかそれ?
赤木 :まあその、結構邪道な感じのことしてるわねこれ、、、雑に説明する
と、このプログラムのソースコード自体の、この文字列定義が終わるところま
でを切り出して、それをその文字列を読んで Crystal のクラス定義のソース
コードを生成するして出力する関数とその呼び出しを付け加えて、それを
Crystal のプログラムとして実行して、その出力結果をコンパイラに渡すのね。
それをやってるのが
学生C:なんかもうちょっと簡単にできそうな気も、、、
赤木 :まあ、なるべく Crystal 自体の機能を使って作ってみたかったんじゃ
ないかしら。 コンパイラがもう一度コンパイラ呼び出して実行までするので、
ちょっと遅いのよねこれ、、、それと、作者氏もこんなややこしい macro 書
くの初めてだから、多分もっとスマートなやり方あるわね。
学生C:で、これ使って書くんですか?やってみますが、、、オプション1つに
つきこの7個全部書くんですか?
赤木 :書かないでも動くものあるかもしれないけど、全部書いて。まあ大した
手間じゃないでしょ?まあこの辺はデザインした人の思想で、ちゃんと他人にも
わかるように書いてね、ということなのよ。
学生C:はあ、、、とりあえずやってみます。
あたりをやったけど、まだ物理系としては調和振動子しか使ってなかったので
色々あんまり気分がでなかったと思うの。なので、今回は、調和振動子
じゃなくて、私たちの業界ではある意味基本の、ケプラー問題をやってみて。
 は1で、太陽の質量は一応設定できる形だけど値は1でね。そうして、
例えば半径1の円軌道だと速度1、周期
は1で、太陽の質量は一応設定できる形だけど値は1でね。そうして、
例えば半径1の円軌道だと速度1、周期 で簡単だから。
で簡単だから。
1:#
2:# integrator library
3:#
4:module Integrators
5: extend self
6: def euler(x,t,h,f)
7: x+=h*f.call(x,t)
8: t+=h
9: {x,t}
10: end
11: def rk2(x,t,h,f)
12:# print "rk2 called\n"
13: k1 = f.call(x,t)
14: k2 = f.call(x+k1*h, t+h)
15: {x + (k1+k2)*(h/2), t+h}
16: end
17:
18: def rk4(x,t,h,f)
19:# print "rk4 called\n"
20: hhalf=h/2
21: k1 = f.call(x,t)
22: k2 = f.call(x+k1*hhalf, t+hhalf)
23: k3 = f.call(x+k2*hhalf, t+hhalf)
24: k4 = f.call(x+k3*h, t+h)
25: {x + (k1+k2*2.0+k3*2.0+k4)*(h/6), t+h}
26: end
27:
28: NITER = 5
29: def gauss4(x, t, h, f)
30: f1 = f.call(x,t)
31: f2 = f1
32: a11 = 0.25
33: a12 = 0.25 - sqrt(3.0)/6
34: a21 = 0.25 + sqrt(3.0)/6
35: a22 = 0.25
36: t1 = t+(a11+a12)*h
37: t2 = t+(a21+a22)*h
38: NITER.times{
39:xg1 = x+(f1*a11+f2*a12)*h
40:xg2 = x+(f1*a21+f2*a22)*h
41:f1 = f.call(xg1,t1)
42:f2 = f.call(xg2,t2)
43: }
44: { x+(f1+f2)*0.5*h, t+h}
45: end
46:
47: def symplectic1a(x,v,h,f)
48: x+= v*h
49: v+= f.call(x)*h
50: {x,v}
51: end
52: def symplectic1b(x,v,h,f)
53: v+= f.call(x)*h
54: x+= v*h
55: {x,v}
56: end
57:
58: def leapfrog(x,v,h,f)
59: f0 = f.call(x)
60: x+= v*h + f0*(h*h/2)
61: f1 = f.call(x)
62: v+= (f0+f1)*(h/2)
63: {x,v}
64: end
65:
66: D1 = 1.0 / (2-exp(log(2.0)/3))
67: D2 = 1 - 2*D1
68: def yoshida4(x,v,h,f)
69: x,v= leapfrog(x,v,h*D1,f)
70: x,v= leapfrog(x,v,h*D2,f)
71: leapfrog(x,v,h*D1,f)
72: end
73:
74: def yoshida6(x,v,h,f)
75: d = {0.784513610477560, 0.235573213359357,
76: -1.17767998417887, 1.31518632068391};
77: 4.times{|i|x,v = leapfrog(x,v,h*d[i],f)}
78: 3.times{|i|x,v = leapfrog(x,v,h*d[2-i],f)}
79: {x,v}
80: end
81:
82:
83:end
84:
85:module SymplecticIntegrators
86: extend self
87: def leapfrog(s, h)
88: s.inc_vel(h*0.5)
89: s.inc_pos(h)
90: s.calc_accel
91: s.inc_vel(h*0.5)
92: end
93: D1 = 1.0 / (2-exp(log(2.0)/3))
94: D2 = 1 - 2*D1
95: def yoshida4(s,h)
96: leapfrog(s,h*D1)
97: leapfrog(s,h*D2)
98: leapfrog(s,h*D1)
99: end
100:
101: def yoshida6(x,v,h,f)
102: d = {0.784513610477560, 0.235573213359357,
103: -1.17767998417887, 1.31518632068391};
104: 4.times{|i|leapfrog(s,h*d[i])}
105: 3.times{|i|leapfrog(s,h*d[2-i])}
106: end
107:end
108:
でどうでしょうか?
1:require "grlib"
2:require "./integratorlib.cr"
3:require "./vector3.cr"
4:include Math
5:include GR
6:def kepler_acceleration(x,m)
7: r2 = x*x
8: r=sqrt(r2)
9: mr3inv = m/(r*r2)
10: -x*mr3inv
11:end
12:def energy(x,v,m)
13: m*(-1.0/sqrt(x*x)+v*v/2)
14:end
15:
16:m=1.0
17:ff = -> (xx : Vector3){ kepler_acceleration(xx,m)}
18:integrator = if ARGV[3]=="LF"
19: STDERR.print "Leap frog will be used\n"
20: -> (xx : Vector3, vv : Vector3, h : Float64){ Integrators.leapfrog(xx,vv,h,ff)}
21: else
22: STDERR.print "Yoshida4 will be used\n"
23: -> (xx : Vector3, vv : Vector3, h : Float64){ Integrators.yoshida4(xx,vv,h,ff)}
24: end
25:
26:n=ARGV[0].to_i
27:norb=ARGV[1].to_i
28:wsize=ARGV[2].to_f
29:h = 2*PI/n
30:t=0.0
31:x= Vector3.new(1.0,0.0,0.0)
32:v= Vector3.new(0.0,1.0,0.0)
33:setwindow(-wsize, wsize,-wsize, wsize)
34:box
35:setcharheight(0.05)
36:mathtex(0.5, 0.06, "x")
37:mathtex(0.06, 0.5, "y")
38:e0 = energy(x,v,m)
39:emax = 0.0
40:while t < norb*PI*2 - h/2
41: xp=x
42: x, v = integrator.call(x,v,h)
43: polyline([xp[0], x[0]], [xp[1], x[1]])
44: t+=h
45: emax = {(energy(x,v,m)-e0).abs, emax}.max
46:end
47:p! -emax/e0
48:c=gets
赤木 :じゃあまた解説お願いできるかしら?

 でいいとのことだったのでそこはさぼってます。
でいいとのことだったのでそこはさぼってます。


ecc=ARGV[4].to_f
x= Vector3.new(1.0+ecc,0.0,0.0)
v= Vector3.new(0.0,sqrt((1-ecc)/(1+ecc)),0.0)
でいいんじゃないかと。例えば  でやってみると、、、あ、1周10ス
テップでは破綻しているので20でやるとリープフロッグで 17%、200にすると
0.26%ですね。離心率が0でなければちゃんと積分公式の次数でエネルギー保存
するんですね。4次公式もちゃんと4桁よくなってます。
でやってみると、、、あ、1周10ス
テップでは破綻しているので20でやるとリープフロッグで 17%、200にすると
0.26%ですね。離心率が0でなければちゃんと積分公式の次数でエネルギー保存
するんですね。4次公式もちゃんと4桁よくなってます。
gravity> keplerplot2 20 10 2 LF 0.5 </dev/null
(-emax) / e0 # => 0.17515575170856668
Leap frog will be used
gravity> keplerplot2 200 10 2 LF 0.5 </dev/null
(-emax) / e0 # => 0.002618881439332199
Leap frog will be used
gravity> keplerplot2 20 10 2 Y4 0.5 </dev/null
(-emax) / e0 # => 0.2662227787182232
Yoshida4 will be used
gravity> keplerplot2 200 10 2 Y4 0.5 </dev/null
(-emax) / e0 # => 2.01715287211357e-5
Yoshida4 will be used
赤木 :離心率 0.9 とか 0.99 とか 0.999 にしたらどうなるかしら?
name: shards
version: 0.1.0
dependencies:
clop:
github: jmakino/clop-crystal
branch: master
grlib:
github: jmakino/gr-crystal
branch: master
nacsio:
github: jmakino/nacsio
branch: master
narray:
github: jmakino/narray
branch: main
にして、
shards install
ってコマンド実行してみて。あ、インターネットにつながってないと駄目よ。
github と書いてあることからわかると思うけど、これ github にアクセスするから。
の3箇所にはおいていて、家のも大学のも raid1 っていう2つのハードディス
クに同じものを書く仕掛けにして、さらに git でバージョン管理して
git のデータも3箇所においてるわ。
Fetching https://github.com/jmakino/clop-crystal.git
Installing clop (0 at master)
こんなのでました。
gravity> crystal lib/clop/src/clopsample.cr
sh: 0: Can't open ./clop_process.sh
[2mShowing last frame. Use --error-trace for full trace.[0m
In [4mlib/clop/src/clop.cr:21:8[0m
[2m 21 | [0m[1m{{system("sh ./clop_process.sh #{l} #{f} #{d} #{strname}")}}[0m
[32;1m^-----[0m
[33;1mError: error executing command: sh ./clop_process.sh 78 "/home/makino/papers/intro_crystal/lib/clop/src/clopsample.cr" "/home/makino/papers/intro_crystal/lib/clop/src" "optionstr", got exit status 127[0m
なんかたりませんといわれてるみたですが、、
gravity> crystal lib/clop/src/clopsample.cr -- -h
sh: 0: Can't open ./clop_process.sh
[2mShowing last frame. Use --error-trace for full trace.[0m
In [4mlib/clop/src/clop.cr:21:8[0m
[2m 21 | [0m[1m{{system("sh ./clop_process.sh #{l} #{f} #{d} #{strname}")}}[0m
[32;1m^-----[0m
[33;1mError: error executing command: sh ./clop_process.sh 78 "/home/makino/papers/intro_crystal/lib/clop/src/clopsample.cr" "/home/makino/papers/intro_crystal/lib/clop/src" "optionstr", got exit status 127[0m
あ、なんかでますね。
gravity> crystal lib/clop/src/clopsample.cr -- -n 10
sh: 0: Can't open ./clop_process.sh
[2mShowing last frame. Use --error-trace for full trace.[0m
In [4mlib/clop/src/clop.cr:21:8[0m
[2m 21 | [0m[1m{{system("sh ./clop_process.sh #{l} #{f} #{d} #{strname}")}}[0m
[32;1m^-----[0m
[33;1mError: error executing command: sh ./clop_process.sh 78 "/home/makino/papers/intro_crystal/lib/clop/src/clopsample.cr" "/home/makino/papers/intro_crystal/lib/clop/src" "optionstr", got exit status 127[0m
なんかでますね。プログラムは、、、なんか一杯かいてありますがこれ文字列変数に値いれているだけで、最後が
clop_init(__LINE__, __FILE__, __DIR__, "optionstr")
options=CLOP.new(optionstr,ARGV)
pp! options
a= options.eps
pp! a.class
pp! a
ですね。 option っていう変数の中に n_particle というメンバー変数があっ
て、それでに 10がはいってますね。
Short name: -n
Long name:--number_of_particles
Value type:int
Default value:none
Variable name:n_particles
Description:Number of particles
Long description:
Number of particles in an N-body snapshot.
とか色々書いてるだけで、 CLOP というクラスができて、その中に
n_particles という変数ができて、コマンドラインから設定できるわけ。
この記述自体は、このオプションの仕様っていうか、どういうものかを
人間にもわかるように書いてあるんだけど、それからクラスとかのコードを
コンパイル時に作るのね。
clop_init(__LINE__, __FILE__, __DIR__, "optionstr")
で、これは普通の関数じゃなくて、コンパイル時に呼び出される関数みたいな
もので、 Crystal ではマクロ (macro)っていうものなの。
C や C++ でいうところのプリプロセッサ指示行みたいなものなんだけど、は
るかに高度なことができるわ。
1:require "grlib"
2:require "./integratorlib.cr"
3:require "./vector3.cr"
4:require "clop"
5:include Math
6:include GR
7:
8:optionstr= <<-END
9: Description: Test integrator for Kepker problem
10: Long description:
11: Test integrator for Kepker problem
12: (c) 2020, Jun Makino
13:
14: Short name: -n
15: Long name: --nsteps
16: Value type:int
17: Default value: 20
18: Variable name: n
19: Description:Number of steps per orbit
20: Long description: Number of steps per orbit
21:
22: Short name: -o
23: Long name: --norbits
24: Value type:int
25: Default value:1
26: Variable name:norb
27: Description:Number of orbits
28: Long description: Number of orbits
29:
30: Short name:-w
31: Long name: --window-size
32: Value type: float
33: Variable name:wsize
34: Default value:1
35: Description:Window size for plotting
36: Long description:
37: Window size for plotting orbit. Window is [-wsize, wsize] for both of
38: x and y coordinates
39:
40: Short name:-e
41: Long name:--ecc
42: Value type:float
43: Default value:0.0
44: Variable name:ecc
45: Description:Initial eccentricity of the orbit
46: Long description: Initial eccentricity of the orbit
47:
48: Short name:-g
49: Long name:--graphic-output
50: Value type: bool
51: Variable name:gout
52: Description:
53: whether or not create graphic output (default:no)
54: Long description:
55: whether or not create graphic output (default:no)
56:
57: Short name:-t
58: Long name:--integrator-type
59: Value type: string
60: Variable name:itype
61: Default value:LF
62: Description:
63: integrator scheme. LF:leapflog, Y4:Yosida4
64: Long description:
65: integrator scheme. LF:leapflog, Y4:Yosida4
66:END
67:
68:clop_init(__LINE__, __FILE__, __DIR__, "optionstr")
69:options=CLOP.new(optionstr,ARGV)
70:
71:def kepler_acceleration(x,m)
72: r2 = x*x
73: r=sqrt(r2)
74: mr3inv = m/(r*r2)
75: -x*mr3inv
76:end
77:def energy(x,v,m)
78: m*(-1.0/sqrt(x*x)+v*v/2)
79:end
80:
81:m=1.0
82:ff = -> (xx : Vector3){ kepler_acceleration(xx,m)}
83:integrator = if options.itype=="LF"
84: STDERR.print "Leap frog will be used\n"
85: -> (xx : Vector3, vv : Vector3, h : Float64)
86: { Integrators.leapfrog(xx,vv,h,ff)}
87: else
88: STDERR.print "Yoshida4 will be used\n"
89: -> (xx : Vector3, vv : Vector3, h : Float64)
90: { Integrators.yoshida4(xx,vv,h,ff)}
91: end
92:
93:h = 2*PI/options.n
94:t=0.0
95:x= Vector3.new(1.0+options.ecc,0.0,0.0)
96:v= Vector3.new(0.0,sqrt((1-options.ecc)/(1+options.ecc)),0.0)
97:if options.gout
98: wsize=options.wsize
99: setwindow(-wsize, wsize,-wsize, wsize)
100: box
101: setcharheight(0.05)
102: mathtex(0.5, 0.06, "x")
103: mathtex(0.06, 0.5, "y")
104:end
105:e0 = energy(x,v,m)
106:emax = 0.0
107:while t < options.norb*PI*2 - h/2
108: xp=x
109: x, v = integrator.call(x,v,h)
110: polyline([xp[0], x[0]], [xp[1], x[1]]) if options.gout
111: t+=h
112: emax = {(energy(x,v,m)-e0).abs, emax}.max
113:end
114:p! -emax/e0
115:c=gets if options.gout
116:
こんな感じですかね。一応動くことは確認してます。前のプログラム
(keplerplot2.cr) と同じパラメータなら同じ答です。離心率がある計算結果
をは、例えば離心率 0.9 で図 16とかその次のみたいな感じです。
Figure 17: 図 16と同じだが1周期1000ステップ。
赤木 :まあそういうものよ。その辺の対応は次回かその次でね。 プログラムのほうは、 8行目から65行目までがオプションの記述ということね。 Description と Long description が同じなところに人間というのは こういうふうにさぼるものかという感慨があるわね。
学生C:英語苦手なんですよ、、、プログラムはあとほとんど前のと同じで、 n とかが options.n に変わるくらいです。あと、 options.gout を使って、 グラフだすかどうか区別してます。
赤木 :そうすると、グラフ書くプログラムはこっちを呼んで、繰り返すよう なのを作ってね。あ、何度も実行するわけだから、 crystal build でコンパ イルして実行ファイル作ってね。
あ、そういえば、 make って知ってる?
学生C:えーと、 make なんとか っていれるとそのなんとかをコンパイルして くれるとかいうものでしたっけ? Makefile というものを書くらしいと、、、
赤木 : 使ったことはない?
学生C: オープンソースのプログラムのインストールとかはしたことあります が、自分のプログラムに使ったことはないです。
赤木 :じゃあ、とりあえず Makefile を以下の2行で作ってみて
% : %.cr
crystal build $<
あ、これ、2行目の crystal の前はタブ1つじゃないと駄目で、空白文字では
駄目なので注意してね。
学生C:作りました。
赤木 : これ、さっきの、CLOP がはいったプログラムの名前は?
学生C: keplerplot3.cr です。
赤木 : じゃあ、make -n keplerplot3 といれてみて?
学生C: はい
crystal build keplerplot3.crとでます。
赤木 :これは、 make に -n というオプションつけると、どのコマンドが実 行されるかだけがでて実行しないのね。なので、 -n とると
学生C:あ、 keplerplot3 ができてますね。
赤木 : もう一度 make してみて
学生C:
make: 'keplerplot3' は更新済みです.とでます。
赤木 :これ、前にコンパイルした時からソースファイルとか関係するファイ ルが新しいかとかをチェックしてるの。なので、実行前は make するようにし ておけばちゃんと最新のが使われるわけ。
学生C: なるほど。
赤木 : まず、離心率 と最初の1周期あたりのステップ数を与えて、10周期ま で積分した時の誤差を、ステップ数2倍にしながら10回繰り返してグラフ書く、っ てどうかしら?あ、折角だから、離心率は複数値与えるようにして。 float vector ってのがあったでしょ?
学生C:じゃあまあ作ってみます、、、
1:require "grlib"
2:require "clop"
3:include Math
4:include GR
5:
6:optionstr= <<-END
7: Description: Test integrator driver for Kepler problem
8: Long description:
9: Test integrator driver for Kepker problem
10: (c) 2020, Jun Makino
11:
12: Short name: -n
13: Long name: --nsteps-initial
14: Value type:int
15: Default value: 20
16: Variable name: n
17: Description:Initial number of steps per orbit
18: Long description: Initial number of steps per orbit
19:
20: Short name: -o
21: Long name: --norbits
22: Value type:int
23: Default value:10
24: Variable name:norb
25: Description:Number of orbits
26: Long description: Number of orbits
27:
28: Short name: -N
29: Long name: --number-of trial-integrations
30: Value type:int
31: Default value:10
32: Variable name:ntry
33: Description:
34: Long description:
35: Number of trial integrations. The timestep is halved at each
36: iteration
37:
38: Short name:-e
39: Long name:--ecc
40: Value type:float vector
41: Default value:0.0,0.3
42: Variable name:ecc
43: Description:values of the eccentricity of the orbit
44: Long description: values of the eccentricity of the orbit
45:
46: Short name:-y
47: Long name:--range-of-y
48: Value type:float vector
49: Default value:1e-15,1e-2
50: Variable name:yrange
51: Description:range of plot of y axis
52: Long description: range of plot of y axis
53:
54: Short name:-t
55: Long name:--integrator-type
56: Value type: string
57: Variable name:itype
58: Default value:LF
59: Description:
60: integrator scheme. LF:leapflog, Y4:Yosida4
61: Long description:
62: integrator scheme. LF:leapflog, Y4:Yosida4
63:END
64:
65:clop_init(__LINE__, __FILE__, __DIR__, "optionstr")
66:options=CLOP.new(optionstr,ARGV)
67:
68:n=options.n
69:system "make keplerplot3"
70:h0 = 2*PI/n
71:setwindow(h0/(1<<options.ntry), h0, options.yrange[0], options.yrange[1])
72:box(10,10, major_x:1, major_y:2, ylog: true, xlog: true)
73:setcharheight(0.04)
74:mathtex(0.5, 0.06, "h")
75:mathtex(0.01, 0.5, "\\Delta E")
76:options.ecc.each{|ecc|
77: hs=Array(Float64).new
78: errs=Array(Float64).new
79: n=options.n
80: options.ntry.times{
81: errs.push `keplerplot3 -n #{n} -e #{ecc} -o #{options.norb} -t #{options.itype}`.
82: split.last.to_f.abs
83: hs.push 2*PI/n
84: n*=2
85: pp! hs
86: pp! errs
87: }
88: polyline(hs, errs)
89:}
90:text(0.2,0.91,"ecc="+options.ecc.join(" ")+", "+options.itype)
91:c=gets
92:
一応できて動いているんじゃないかと、、、こんなグラフがつくれます。
Figure 19: 図 18 と同じだが4次公式。
学生C: 63行目まではまたオプション定義です。n, o, e, y, t とあって、 もうそのテキストに書いてある通りですが、1周期あたりのステップ数の初期 値、積分する軌道周期、離心率(コンマで区切って複数与える)、グラフ書く時 の y 軸の最小、最大値、使う積分公式です。
赤木 :一杯あるわね。
学生C:あ、そうかもしれません。ふやすのが簡単なのでつい、、、
赤木 :まあそういうふうに使うために作ったものだから、それでいいのよ。 なるべくプログラムは柔軟に、同じようなことだけどちょっとだけ違う、とい うのはパラメータで変えるように、とすると間違いも少ないわ。
学生C:はあ、そうかもしれません。69行目の system は、文字をOSのコマン ドとして実行するものです。ここでは make かけて最新のソースからコンパイ ルします。本当はコンパイルエラーになったら止めるとかあるべきかもしれな いですがさぼってます。
その後はグラフのレンジ決めて枠書いてラベル書くのが75行目までですね。76 行目の each で離心率の値毎のその中を実行で、その中は、線引くのに使う配 列を 77,78 行列で空にして、80行目が ntry 回ステップサイズ変えながら繰り返す、で、 81行で keplerplot3 を実行します。 実行するのは system と同じですが、ここではバッククォートで文字列例を囲 んでいて、これは実行結果の出力を文字列として返すものです。Ruby にもあっ てもっと古い言語にもあるんですかね?
赤木 :perl にはあったわね。
学生C:文字列の中で #{n} とかしているのは、そこが {}の中の式の値、文字 型でなければ to_s で文字列にしたもの、に置き換わるものです。これも Ruby と同じですね。で、その文字列を split.last.to_f.abs で、これは スペースで区切りがあるとして配列に変換、配列の最後の要素、それを 浮動小数点に変換、絶対値、と順番に関数適用ですね。その結果を 配列 errs に追加するという格好です。
赤木 : ピリオドの後で改行してもいいのね。
学生C: やったら大丈夫でした。で、その次で時間刻みも配列にいれて、85行 で n を2倍にします。その後は計算できてそうかどうか画面にだしてるだけです。 で、89行でデータの線をひきます。これで本体はおしまいですね。
あ、離心率の値と積分公式もグラフにあったほうがいいかなと思って、91行の text をつ けました。
赤木 : なるほど。あとはグラフのどの線がどの値かがわかるようななにかを つければ、このグラフなら論文にあってもおかしくないわね。
学生C:(赤木さんのいうこと信用できるのかな、、、)
赤木 :これ、とにかく、離心率ちょっと大きくなると誤差がものすごく大き くなるのがわかるわね?リープフロッグでも、0.3から0.9までで4桁、 4次公式だと6桁くらい悪いのね。これどうしてかわかる?
学生C:読者の演習問題ということでどうでしょうか?
赤木 :そうねえ、、、
学生C:(逃げる)
https://github.com/jmakino/clop-crystal 9.1. 課題
9.2. まとめ
9.3. 参考資料