7. 2次と4次のルンゲクッタ法
赤木 :オイラー法もちょっと飽きたから、もう少し賢い方法をやってみて。2 次と4次のルンゲクッタね。
学生C:4次ってどんなのですか?
赤木 :これ。


学生C: 微分方程式を受け取るってどういうことですか?
赤木 : 微分方程式を関数で表現して、その関数をルンゲクッタ法の関数に渡すわけ。
学生C: すみません、何いわれてるのかわかりません。
赤木 : じゃあちょっと順番に、微分方程式を関数にしてみて。オイラー法で。
学生C:前の
1:include Math
2:x=1.0; v=0.0; k=1.0
3:n=ARGV[0].to_i
4:h = 2*PI/n
5:p! h
6:t=0
7:n.times{
8: dv = -x*k*h
9: x+= v*h
10: v+= dv
11: t+= h
12:}
13:p! [x, v, t]
14:p! [x-cos(t), v-sin(t)]
で、微分方程式は  だから、 x, v, k が
入力で時間導関数が出力な関数ですね。えーと、出力が2つの関数って書ける
んですか?
だから、 x, v, k が
入力で時間導関数が出力な関数ですね。えーと、出力が2つの関数って書ける
んですか?
赤木 : できるかできないかというとできるんだけど、でも、上のルンゲクッ タの数式自体が、 x とか f とか k はスカラーではなくてベクトルじゃない? だから、ベクトル使うほうが自然でしょ?
学生C:でも、今まで3次元ベクトルしかやってないし、ここで必要なのは2次 元だし、2次元問題になったら4次元ベクトルがいりますねよね?
赤木 :そうね、なので、一般の次元のベクトルを、あんまり実行効率よくな いかもだけど作っておいて。
学生C:作っておいてといわれましても、、、 赤木 :と、そうね。ここでは、Array から新しい型を作ることを考えるわね。 オブジェクト指向言語でいう「継承」ってやつ。なんか難しいそうなんだけど、 要するに、Array と同じ機能をもつ新しいクラスを作って、それに演算とかメ ソッドを追加するの。加算だけ書いてみるとこんな感じ:
class MathVector(T) < Array(T)
def +(a)
self.map_with_index{|x,k| x+a[k]}.to_mathv
end
end
class Array(T)
def to_mathv
x=MathVector(T).new
self.each{|v| x.push v}
x
end
end
最初の
class MathVector(T) < Array(T)は、Array を継承して MathVector というクラスを作ります、というものね。 Ruby だと
class MathVector < Arrayなんだけど、ここは Crystal では ちょっと違うの。ここで (T) は、Array はさらに何かクラスをパラメータと してもつ、ということで、つまり、整数の Array とか実数の Array とかを Array(Int32) とか Array(Float64) とかで作れるわけ。逆に、必ず Array が どういうクラスの要素をもつか、を決めておかないといけないから、Ruby み たいに何もない Array を [] とかで作れなくて、Array(Int32).new とかしな いといけないの。
学生C: なんか面倒そうですね。Ruby のほうがよくないですか?
赤木 : まあこれについては空集合をなんかうまいことやってくれないの?と いう気もするわね。でも、そのかわり100倍とかそれ以上実行速度が速いから、、、
学生C:はあ、、、
赤木 :でも実行速度は重要よ。1分で終わるものが1時間かかったらやる気にならないもの。
学生C:そうなんですが、、、
赤木 :で、3行目の
self.map_with_index{|x,k| x+a[k]}.to_mathv
が + メソッドの本体ね。map_with_index は Array のメソッドで、各要素と
その添字から計算した値を要素とする Array を返すのね。なので、 Array に
なっちゃうから、 Array を MathVector に変換するメソッド to_mathv を
Array のほうに作っておくの。これ、もうちょっと上手く書ける気がするけど、
私よくわかってないから、上の話ででてきたの要素がない MathVector をまず
作って、で、それに Array のほうの要素を1つづつ追加して、としてるの。
学生C:なんかややこしいですね、、、実行遅いんじゃないですか?
赤木 :まあ素晴らしく速いわけではないわね。速くする話はもうちょっと先 でするわ。とりあえず、これで、 - と、単項の -,+ と、あとスカラーとの掛 け算 *(a) を作っておいて。
あと、Float のほうにも、 MyVectorとの掛け算がないと掛け算に順序ができ ちゃうから、 vector3.cr の時と同じように Float との乗算も作っておいて ね。
学生C:はあ、、、こんなんですかね。
1:class MathVector(T) < Array(T)
2: def +(a) self.map_with_index{|x,k| x+a[k]}.to_mathv end
3: def -(a) self.map_with_index{|x,k| x-a[k]}.to_mathv end
4: def -() self.map{|x| -x}.to_mathv end
5: def +() self end
6: def *(a) self.map{|x| x*a}.to_mathv end
7:end
8:
9:struct Float
10: def *(a : MathVector(T)) a*self end
11:end
12:
13:class Array(T)
14: def to_mathv
15: x=MathVector(T).new
16: self.each{|v| x.push v}
17: x
18: end
19:end
赤木 :で、それ使って、まず微分方程式書いて。
学生C:x が 長さ2で  がはいったベクトル、 k は係数のスカラーとして
がはいったベクトル、 k は係数のスカラーとして
def harmonic(x,k)
[x[1], -k*x[0]].to_mathv
end
ですか?ベクトル返す必要があるから2要素の配列にしてから .to_mathv つけてみてます。
赤木 :式はあってる気がするからコンパイルできれば、、、
学生C:
require "./mathvector.cr"
def harmonic(x,k)
[x[1], -k*x[0]].to_mathv
end
p! harmonic([1.0,0.5].to_mathv, 1.0)
でそれっぽい [0.5, -1.0] がでたから大丈夫ではないかと、、、
赤木 :テストしておくのはよいことね。じゃあ、次はこの関数使ってオイラー
法のプログラムを書き直してみて。あ、あと、刻み幅を、 1/100 から
 まで、プログラムの中でループ回して、刻み幅と誤差をだすように
してみて。繰り返しは、前もでてきたけど、
まで、プログラムの中でループ回して、刻み幅と誤差をだすように
してみて。繰り返しは、前もでてきたけど、
n.times{ ...}
で n 回繰り返す、ってのを使いましょう。
学生C:うーん、、、
1:include Math
2:require "./mathvector.cr"
3:
4:def harmonic(x,k)
5: [x[1], -k*x[0]].to_mathv
6:end
7:n=100
8:5.times{
9: h=1.0/n*PI
10: t=0.0
11: x=[1.0,0.0].to_mathv
12: k=1.0
13: while t< PI*2 - h/2
14: x += harmonic(x,k)*h
15: t+= h
16: end
17: print "h= ", h, " errors= ",x[0]-cos(t), " ", x[1]-sin(t), "\n"
18: n*=10
19:}
こんな感じでしょうか。実行すると
gravity> crystal harmonic-euler-with-function.cr h= 0.031415926535897934 errors= 0.10367468781049172 0.0022800427262427655 h= 0.0031415926535897933 errors= 0.009918420171222575 2.0875749940652505e-5 h= 0.0003141592653589793 errors= 0.0009874475970643726 2.0691472301136493e-7 h= 3.1415926535897935e-5 errors= 9.870091457697683e-5 2.0817890742914563e-9 h= 3.141592653589793e-6 errors= 9.86965309146548e-6 4.5341698913228974e-11赤木 : なかなかよい感じね。オイラー法が
x += harmonic(x,k)*h
で書けてて、もとの数学的定義に近いから、わかりやすくない?
学生C:まあ、それはそうですね。
赤木 :じゃあ次はこれを2次ルンゲクッタにしてみて。
学生C:えーと、なので、
x += harmonic(x,k)*h
のところも、数式と同様
k1 = harmonic(x,k)
k2 = harmonic(x+k1*h, k)
x += h/2*(k1+k2)
とすればいいわけですよね?なので、
1:include Math
2:require "./mathvector.cr"
3:
4:def harmonic(x,k)
5: [x[1], -k*x[0]].to_mathv
6:end
7:n=100
8:5.times{
9: h=1.0/n*PI
10: t=0.0
11: x=[1.0,0.0].to_mathv
12: k=1.0
13: while t< PI*2 - h/2
14: k1 = harmonic(x,k)
15: k2 = harmonic(x+k1*h, k)
16: x += h/2*(k1+k2)
17: t+= h
18: end
19: print "h= ", h, " errors= ",x[0]-cos(t), " ", x[1]-sin(t), "\n"
20: n*=10
21:}
こんな感じでしょうか。実行すると
gravity> crystal harmonic-rk2-with-function.cr h= 0.031415926535897934 errors= 2.3818764601557518e-5 -0.0010332614065876578 h= 0.0031415926535897933 errors= 2.429886425403538e-8 -1.0335394959216679e-5 h= 0.0003141592653589793 errors= 2.4347190930029683e-11 -1.0335214253967046e-7 h= 3.1415926535897935e-5 errors= 7.549516567451064e-15 -1.0190453008868347e-9 h= 3.141592653589793e-6 errors= 2.6645352591003757e-15 1.4413227284901166e-11おお、確かにすごく精度あがってますね。
赤木 :そうね。で、あと、考えて欲しいのは、このオイラー法やルンゲクッ タ法自体を関数にする、この関数は微分方程式の関数を引数として受け取る、 ということなの。そうできると、微分方程式と数値積分法が独立に定義できる から、それぞれをベクトル型の定義と同じように別々に作っておいておけるし、 一つのプログラムで数値積分法を切換える、といったこともできるじゃない。
このあとで色々そういうことをやってもらうから、この辺から入門みたいなね。
学生C:はあ、、、えーと、関数を引数でもらうというと、Fortran ではいき なり名前で渡せましたが Crystal ではどうするんですか?
赤木 :そうね。これ割合ややこしいところで、 Proc クラスというのを使う の。Ruby だと、コンパイルしないで実行時に実行できればいいから、関数の 引数の型とか気にしないで適当に渡す文法なんだけど、Crystal では 渡す関数の引数の型を指定して、他の関数とかに渡せる形にする文法があるの。 例えば
f = -> (xx : MathVector(Float64), t : Float64){ harmonic(xx,k)}
とすると、 f が、ベクトル x とスカラー t を引数にとって、関数 harmonic
にそれを渡してその結果を返すもの、ということになるの。但し、 f そのも
のは普通の関数ではないので、 f(x,t) じゃなくて f.call(x,t) というふう
に使うの。
あ、だから、これ、 {} の中は別に関数1つしか書けないわけじゃなくて、なんでも書けるのね。それから、
k=1.0
f = -> (xx : MathVector(Float64) ){ harmonic(xx,k)}
みたいなこともできるの。
学生C:これあとで k の値が変わったらどうなるんですか?
赤木 :良いところに気が付いたわね。この f ができた時に k は1だったわけ で、それを憶えてるの。なので、あとで k 変えても f は k=1 のままで動くわ。 だって、変わって欲しいならちゃんと k 渡せばいいんだもの。
学生C:なるほど。tはどこにいっちゃうんですか?
赤木 :これ、ルンゲクッタ公式としては t があるんだけど、今解く微分方程 式には t がないわけね。なので、ルンゲクッタ公式のプログラムは tが引数にある関数がほしいから、そういう定義をして、{} の中では xx と t があるんだけど、実際の関数は harmonic は t 使わないから 単に無視されるわけ。
学生C:harmonic(xx,k) から 引数が(xx,t) である別の関数を作って、それを 積分公式に渡す、みたいな感じですね。なんかちょっと複雑な気がしますが、、、
赤木 :他の言語だと lambda とか使って、もっとわけのわからない書き方だっ たりするから、 Ruby 由来の書き方の Crystal はわりとわかりやすいかな。 C++ だと C++14 になってラムダ式ができて、こんな感じ:
auto plus = [](int a, int b) { return a + b; };
int result = plus(2, 3); // result == 5
[]が謎だけどあとは Crystal の記法から想像つくでしょ?普通の関数みたい
に見えて call とかつかないのが特殊ね。
まずはオイラー法を関数にしてみて。 x, t, h, それから微分方程式 として f を受け取るのね。で,fは t も引数で f.call(x.t) となるとして。
学生C:そしたら、
def euler(x,t,h,f)
x+= h*f.call
x
end
とかですか?
赤木 :そうね、それはそれでいいんだけど、 t もアップデートして返すようにできない?
学生C:2つ返す方法ってあるんでしたっけ?
赤木 :Ruby だと配列にして返すとなんかできたんだけど、Crystal なのでタ プル使ってみて。
[x.t]の代わりに
{x,t}
と書くの。これは Ruby にはなくて Crystal にあるのは、タプルは作ったあ
とで要素に代入とかできなくて、型推論とか簡単だからかしらね。配列で書い
てもできないわけじゃないんだけど、例えば
1:def test
2: {[1,2,3], "abc"}
3:end
4:a,b =test
5:p! a
6:p! b
で、
gravity> crystal testtupple.cr a # => [1, 2, 3] b # => "abc"みたいなことができるわけ。
学生C:そうすると、こんな感じでしょうか?
def euler(x,t,h,f)
x+= h*f.call
t+=h
{x,t}
end
赤木 :そうね、これでまったく正しくて全然問題ないんだけど、x とか t っ
て別に代入しなくても、返す値計算すればよくて、タプルの中に式書けるから、
もうちょっと簡単にならないかしら?
学生C: 式を直接、ということですね、えーと、、、、
def euler(x,t,h,f)
{x+h*f.call, t+h}
end
ですか?
赤木 :それでコンパイル通って実行できれば多分。2次ルンゲクッタは?
学生C:えーと、同じようにするなら、、、
def rk2(x,t,h,f)
k1 = f.call(x,t)
k2 = f.call(x+k1*h, t+h)
{x + h/2*(k1+k2), t+h}
end
でしょうか?
赤木 :多分。じゃあ、さっきのプログラムで、積分スキームについても2通りやるようなプログラムにしてみて。
学生C:(注文多いな、、、)はい。
1:include Math
2:require "./mathvector.cr"
3:
4:def harmonic(x,k)
5: [x[1], -k*x[0]].to_mathv
6:end
7:def euler(x,t,h,f)
8: x+=h*f.call(x,t)
9: t+=h
10: {x,t}
11:end
12:def rk2(x,t,h,f)
13: k1 = f.call(x,t)
14: k2 = f.call(x+k1*h, t+h)
15: {x + h/2*(k1+k2), t+h}
16:end
17:
18:["Euler", "RK2"].each{|name|
19: n=100
20: print "Result for ", name, " method\n"
21: 5.times{
22: h=1.0/n*PI
23: t=0.0
24: x=[1.0,0.0].to_mathv
25: k=1.0
26: f = -> (xx : MathVector(Float64), t : Float64){ harmonic(xx,k)}
27: while t < PI*2 - h/2
28: if name == "Euler"
29: x, t = euler(x,t,h,f)
30: else
31: x, t = rk2(x,t,h,f)
32: end
33: end
34: print "h= ", h, " errors= ",x[0]-cos(t), " ", x[1]-sin(t), "\n"
35: n*=10
36: }
37:}
一応動いたので大丈夫ではないかと、、、
gravity> crystal harmonic-multischemes.cr Result for Euler method h= 0.031415926535897934 errors= 0.10367468781049172 0.0022800427262427655 h= 0.0031415926535897933 errors= 0.009918420171222575 2.0875749940652505e-5 h= 0.0003141592653589793 errors= 0.0009874475970643726 2.0691472301136493e-7 h= 3.1415926535897935e-5 errors= 9.870091457697683e-5 2.0817890742914563e-9 h= 3.141592653589793e-6 errors= 9.86965309146548e-6 4.5341698913228974e-11 Result for RK2 method h= 0.031415926535897934 errors= 2.3818764601557518e-5 -0.0010332614065876578 h= 0.0031415926535897933 errors= 2.429886425403538e-8 -1.0335394959216679e-5 h= 0.0003141592653589793 errors= 2.4347190930029683e-11 -1.0335214253967046e-7 h= 3.1415926535897935e-5 errors= 7.549516567451064e-15 -1.0190453008868347e-9 h= 3.141592653589793e-6 errors= 2.6645352591003757e-15 1.4413227284901166e-11赤木 :よさそうね。結果をは前のと同じになってるわね。 あとは、4次のルンゲクッタと、数値だけみてても気分がでないので、グラフよね。
学生C:4次は、、、あ、式もらってますね。
1:include Math
2:require "./mathvector.cr"
3:require "grlib"
4:include GR
5:
6:def harmonic(x,k)
7: [x[1], -k*x[0]].to_mathv
8:end
9:def euler(x,t,h,f)
10: x+=h*f.call(x,t)
11: t+=h
12: {x,t}
13:end
14:def rk2(x,t,h,f)
15: k1 = f.call(x,t)
16: k2 = f.call(x+k1*h, t+h)
17: {x + h/2*(k1+k2), t+h}
18:end
19:
20:def rk4(x,t,h,f)
21: hhalf=h/2
22: k1 = f.call(x,t)
23: k2 = f.call(x+k1*hhalf, t+hhalf)
24: k3 = f.call(x+k2*hhalf, t+hhalf)
25: k4 = f.call(x+k3*h, t+h)
26: {x + (h/6)*(k1+k2*2+k3*2+k4), t+h}
27:end
28:
29:setwindow(3e-5, 7e-2, 1e-14, 1e-1)
30:setscale(3)
31:box(x_tick:100,y_tick:100,major_y:2,xlog: true, ylog: true)
32:
33:["Euler", "RK2", "RK4"].each{|name|
34: n=100
35: print "Result for ", name, " method\n"
36: ha=Array(Float64).new
37: ea=Array(Float64).new
38: 10.times{
39: h=1.0/n*PI
40: t=0.0
41: x=[1.0,0.0].to_mathv
42: k=1.0
43: f = -> (xx : MathVector(Float64), t : Float64){ harmonic(xx,k)}
44: while t < PI*2 - h/2
45: if name == "Euler"
46: x, t = euler(x,t,h,f)
47: elsif name == "RK2"
48: x, t = rk2(x,t,h,f)
49: else
50: x, t = rk4(x,t,h,f)
51: end
52: end
53: ex = x[0]-cos(t)
54: ey = x[1]-sin(t)
55: print "h= ", h, " errors= ",ex, " ", ey, "\n"
56:# ha.push log(h)/log(10)
57:# ea.push log((x[0]-cos(t)).abs)/log(10)
58: ha.push h
59: ea.push sqrt(ex*ex+ey*ey)
60: n*=2
61: }
62: p! ha
63: p! ea
64: polyline(ha, ea)
65:}
66:setcharheight(0.04)
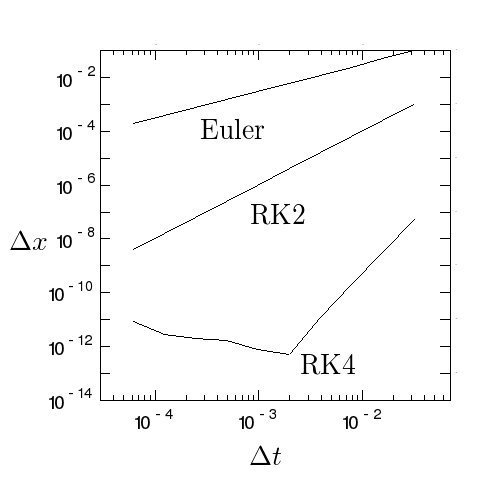
67:mathtex(0.5,0.07,"\\Delta t")
68:mathtex(0.02,0.5,"\\Delta x")
69:mathtex(0.4,0.72,"\\rm Euler")
70:mathtex(0.5,0.55,"\\rm RK2")
71:mathtex(0.6,0.25,"\\rm RK4")
72:
73:c=gets
グラフだしてみました。
赤木 :プログラム解説してみて。読者の皆様(いるのかそんなの?)向けに。
学生C:はい。最初の2行は今までと同じで数学関数とベクトル型使います宣 言で、次の2行は GR の同じような使います宣言です。
あと、6-15行は前と同じなので省略します。20-27 が4次ルンゲクッタですね。 2次と同じように、ほぼ数式の通りです。
29-31 はグラフ書く準備で、setwindow(xmin, xmax, ymin, ymax) は x軸、y 軸の範囲、 setscale は引数の1ビット目が x軸、2ビット目がy軸を対数にす るかどうかです。 box は作者が適当に作った関数で、 GR のいくつかの関数 呼んで枠を書くものですね。 x_tick:100 みたいに 名前:値 という形式なの は、デフォルトの値がある引数に、呼ぶ時の順番とは無関係に値を与えるやり 方みたいです。
赤木 :あら、よく気が付いたわね。
学生C:著者のサンプルがそうなってたので。どんどんいくと、 33行は RK4 がはいっただけで前と同じですね。 36, 37 行で、プロットするデータをいれる配列を長さ0で作ります。 そのあと52行目までは前のと同じで、53, 54 行で誤差の x, y 成分を計算し て、 58, 59 で時間刻みと誤差の絶対値を配列にいれます。
で、64行で線ひいて、グラフはできたことになります。
最後に66行以降で軸のラベルや線がどの積分公式かのラベルつけます。これは LaTeX の数式モードになるらしいので、 \Delta t とか使えますがそのかわり なんでもイタリックになるので、ならないように \\rm Euler としてます。 LaTeX なら \rm ですが、\\rm となるのは文字列渡す時に \\ でないと \ が実際には渡らないからです。
あと、結果ですが、傾きがオイラー、ルンゲクッタ2、4次でそれぞれちゃんと 1, 2, 4 くらいなので、多分ちゃんとできてるのではないかと、、、
赤木 :テキスト出すのは別の関数もあったはずね。でもまあ、大変結構。
これ、4次ルンゲクッタで、h 小さくしても途中から精度上がらなくなるのど うしてかわかる?
学生C:えーと、丸め誤差でしたっけ?
赤木 :そう。今これ、Float64 で計算しているのね。これは IEEE-754 とい う規格に従っていて、実数を符号1ビット、指数11ビット、仮数52ビットで表 すの。仮数は 1と2の間に52ビット使うから、1の時に大体 $10^{-16}$ の精度 があるわけ。
それより精度が落ちて$10^{-12}$ くらいになってるのは、数千ステップ計算 しているからね。
これ、何故そんなに落ちるのかとかもうちょっと落ちないようにできないのかとか色々わりと大事な話があるんだけど、その辺またあとでね。
次 回は、ちょっと違うタイプの時間積分法ね。お疲れさま。あ、あと、オイラー 法とかルンゲクッタ法とかがどういうものかはあんまり説明してないわね。 ちょっと古いけどこの辺そんなに変わってないので、 著者の昔の講義資料の3回目くらいまでみておいてね。
システム数理IV講義資料 http://jun-makino.sakura.ne.jp/kougi/system_suuri4_1999/overall.html
gr-crystal https://github.com/jmakino/gr-crystal|gr-crystal 7.1. 課題
7.2. まとめ
7.3. 参考資料