世の中には陰解法というものがあるのは数値計算をやっている人は大抵ご存じ
でしょう。陰解法とは、ある系の時間発展を解く、つまり未来の状態を求める
のに、未来の状態自体の満たす方程式を解く方法です。これは、未来の状態を
使わない方法(陽解法)に対応する言葉です。例えば、1次元の熱伝導の方程
式
を解くのに、以下のような差分化をするのが陽解法です。(式は適当に書いてるので間違ってるかもしれません)
この方法は簡単でよいのですが、空間刻み 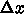 を小さくすると、そ
の自乗に比例して時間刻み
を小さくすると、そ
の自乗に比例して時間刻み 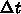 を小さくしないといけない、という
問題があります。これはフォン・ノイマンの安定性条件といわれるものです。
この限界より大きな時間刻みでは解が発散します。
を小さくしないといけない、という
問題があります。これはフォン・ノイマンの安定性条件といわれるものです。
この限界より大きな時間刻みでは解が発散します。
陰解法のもっとも簡単な形は
です。これは  の全部についての連立方程式になっていますが、1次
元の場合は簡単に解けるのであまり問題はありません。で、この形では、時間
刻みをどんなに大きくとっても解が不安定になることはない、ということが知
られています。
の全部についての連立方程式になっていますが、1次
元の場合は簡単に解けるのであまり問題はありません。で、この形では、時間
刻みをどんなに大きくとっても解が不安定になることはない、ということが知
られています。
拡散や熱伝導だとまあこうするしかないみたいなところもあるのですが、陰解
法は流体の数値計算でも広く使われています。これは、流体では CFL 条件と
いうものがあり、陽解法では時間刻みが  (ここで
(ここで  は音
速)を超えられないからです。
は音
速)を超えられないからです。
超音速のロケットやミサイルの数値計算ならどうせこの条件が効くのですが、
音速よりずっと遅い流れを解く時にはこれは問題です。例えば風速 1m/s の流
れを解くのに、CFL条件で決まるステップサイズでは1ステップで風は空間刻み
の1/300 しか進まないことになり、計算量がとてつもなく増えてしまいます。
この時に、「音速が無限に大きい」という近似、いわゆる非圧縮近似をすると、
陰的な方程式を解く必要がでてくる代わりに時間刻みを大きくとれることにな
ります。但し、陰的な方程式として、ポアソン方程式がでてきて、これを
離散化した連立一次方程式を時間ステップ毎に解く必要が発生します。
空間1次元の場合には、上の熱伝導の方程式と同じようにポアソン方程式を簡
単に解くことができるのですが、2次元や3次元になるとそうはいきません。
普通に連立方程式をガウスの消去法にあたる方法で計算すると、1次元の場合
と違って計算量がものすごく増えてしまうからです。このため、直接法
は諦めて反復法を使うわけです。
もちろん流体計算だけが反復法の応用先ではありませんが、大規模な
反復法の主要な応用であるのも間違いありません。反復法の研究は
そういうわけで数値解法研究の最大分野といってもよく、昔は SOR 法
とかも使われていましたが最近は CG 法とマルチグリッド法がよく使われます。
が、最近の計算機での効率的な計算、という観点からは、陰解法、反復法、と
いうのは極めて厄介なものです。理由は沢山ありますが、いくつかをあげると、
-
空間分解能をあげていった時に、収束が遅くなり計算量がどんどん増える。
場合によってはそもそも収束しなくなる。
-
高いメインメモリのバンド幅を要求する。基本的に、反復計算は差分スキームによっ
て与えられる疎行列とベクトルの積になるので、規則格子でも B/F=1 程度
は最低限必要になる。
-
CG法では反復毎にベクトルの内積をとる必要があり、これは全計算ノード
にわたる縮約になる。
といったものです。この1つだけでも結構致命的なのですが、現状では三重苦
というところです。
さて、亜音速の流体を解くことをもう一度考えてみると、レイノルズ数
が同じであれば、マッハ数が 0.5 くらいから下なら流れは実際上同じになる、
というのが流体力学の基本です。もちろん、この事実があるので、非圧縮近似
というものが成立するわけです。
しかし、ということは、逆の近似もできるはずです。つまり、 1m/s の流れを
解くのなら、音速が 340m/s ではなく 2m/s であるような「空気」を考えても
いいはずです。そうすると、 CFL 条件が 170倍ゆるくなって、陰解法を使う
までもなくなります。
このことは大昔からわかっていてもよさそうなのですが、最近まで実際の数値
計算にはあまり使われていなかったようです。この方法で大成功をしたのが
この3月に東大地惑で博士をとった堀田さんで、太陽の対流圏の計算にこの
音速を遅くする方法(音速抑制法)を採用し、世界で初めて1次元方向のメッシュ
数が3000にも及ぶシミュレーションに成功しました。それにより、太陽の対流
圏の構造の理解が大きく進展しました。これは「京」を使った成果でもありま
す。
太陽の計算では話はちょっと複雑です。単純に音速を落とすと、状態方程式が
柔らかくなってしまって太陽の密度構造がつくれないからです。なので、
密度構造を表現する状態方程式と、ダイナミクスの表現にはいる状態方程式を
分離しています。
普通の工学的な応用であれば、空気への重力はそもそも無視できるため、単純
に音速を落とすだけで十分です。
このような方法は、原理的には、実際には有限の何かが無限大である、という
近似をして解いているあらゆる系に対して使うことができます。亜音速流体
の場合には非圧縮近似の代わりに遷音速近似というべきものを使ったわけです。
同じような近似が原理的には可能なはずの例はマントル対流です。マントル対
流では、太陽の対流圏ともまた違い、粘性がものすごく大きいためにレイノル
ズ数が非常に小さくなります。このため、流体の運動方程式から慣性項を消去
し、浮力と粘性が釣り合う、という陰的な方程式を解いています。これはまあ
それ自体それほど大変ではないのですが、マントル対流の困難は粘性が温度に
よって何桁も変わるところにあり、これはほとんどの反復法を破綻させます。
といって、陽解法だと、CFL条件では地震波を解くような時間刻みで10億年で
動くマントル対流を、となってどうにもならないわけです。
さて、慣性項を消す、という近似ができるということは、慣性項を大きくする、
という近似もできる、ということです。レイノルズ数が1よりある程度小さけ
れば流れはいわゆるストークス流ですから、慣性項の大きさがなんでも答は同
じです。
このやりかたでは慣性項を大きくするだけなので、状態方程式は変えません。
なので、圧力平衡も問題なく計算できます。太陽ではこれは駄目で、それはレ
イノルズ数が始めから大きいからです。また、温度によって粘性が変わるのに
も、温暖によって慣性項を変えることで対応できます。
マントル対流の場合には熱伝導と粘性がそれぞれ拡散方程式の形になるので、
それぞれについてフォンノイマン条件がさらにでてきて、話がさらにもうちょっ
とややこしくなります。但し、これは、熱伝導係数と粘性係数を、解が変わら
ないように同時に変えることが可能なので、両方のフォンノイマン条件が
同じになるようにするとかなり大きな時間刻みがとれます。
と、この辺は昨年度に私のところで卒研をやった竹山君が導出した話です。実
際に数値実験もやっていて、本当かよという気もするのですがどうも上手くい
くようです。
同じような扱いが、おそらくもっと色々なことに使えるでしょう。例えば
-
放射伝達(光速をすごく遅くする)
-
化学反応とカップルした流体(化学反応も必要に応じて遅くする)
-
単純な放射冷却(問題ない範囲で冷却を遅くする)
といったことがすぐに考えつくところです。このような近似のメリットは、上
に書いた三重苦が全部ひっくりかえることで、
-
空間分解能をあげても時間刻みはあまり小さくしなくていいし、反復しな
いので収束性の問題はない。
-
メインメモリのバンド幅をあまり要求しない。陽解法の流体スキームは
高次精度では計算量が多く、B/F が小さな計算機でも高い性能がでる。
-
全計算ノードにわたる縮約が不要である。
これはあまりに夢のような話で、書いてて信じられないところもありますが、
相当色々なところで上手くいくのではないかと思います。