79. Anton (2010/1/14, 2010/1/16 追記)
Anton は、 D. E. Shaw Research (DESRES) で開発した古典 MD 専用計算機です。相互
作用計算のところは専用パイプラインでやるというもので、その辺は
MD-GRAPE と同じですが、結構違うのは、MD-GRAPE は相互作用計算以外はホス
ト計算機でやるのに対して Anton ではそれもやるためのプログラム可能なプ
ロセッサコアも集積したことと、近距離相互作用計算を並列、高速に行うため
の専用ネットワークも設計して、ネットワークインターフェースまでチップに
集積したことです。
そこまでやった理由は、比較的少ない、 10 万程度の粒子数で非常に高速に計
算したい、というものでした。その成果は結構なもので、 2 万原子程度だった
と思いますが1ステップを数十マイクロ秒というところまで高速化しています。
これは SC09 でゴードンベル賞を獲得しています。他の普通の並列計算機では、
BG/P とかでもまだ 1 ステップ1ms 程度なので、桁違いに速いわけです。これ
だけ速くした、特にレイテンシを切り詰められたのはプログラム可能なプロセッ
サとネットワークまで作りこんで、前回、前々回に書いたようなメモリ階層に
よるオーバーヘッドを避けたことが大きな理由ではありますが、それだけでも
ありません。
論文
にあるように、相互作用の計算の並列化に新しい方法を使っています。これに
より、並列度を上げた時の通信負荷を大きく下げて、現実的な
配線本数でシステムを構築可能にしています。
どういう方法かを以下にまとめます。近距離相互作用なので限界距離があります。今、簡単のために並列化のための領域分割の領域の大きさ(一辺の
長さ)がこの限界距離と同じだとします。そうすると、ある1つのプロセッサは、
自分への力を計算するためには基本的に周りの
今、もっとプロセッサを沢山使うために、領域のサイズを限界距離の 1/2 に
したとします。プロセッサ数は 8倍です。この時には、 26 個ではなくて 124
個のプロセッサからデータをもらってくることになります。1プロセッサの
データ量は 1/8 になるので、1ステップ当りの通信量は 0.6 倍くらい、計算
量は 1/8 になるので、計算に対して通信を5倍くらい速くしないといけないこ
とになります。これはつまり、プロセッサ数を領域数より多くするのは結構困
難である、ということを意味します。
DESRES のグループは、「あるプロセッサが、もらってきた粒子同士の相互作用
計算もできるものはする」というふうにすれば全部をもらってくる必要がなく
なる、ということを使って通信量を減らしています。最初の、領域の一辺の長
さが限界距離と同じ場合を考えます。自分の横にあるものは斜めも含めて8個も
らってくるけど、上下は真上と真下の2個だけをもらってきたとしましょう。そ
うすると、例えば真上の領域の粒子と、自分と同じ高さの9個の領域との相互作
用を自分が計算することができるので、これを計算して上のプロセッサに送り
返すことができます。また、下のプロセッサについても、同様に下のプロセッ
サの領域と自分とその横の領域の相互作用を計算して、合計して下に送り返す
ことができます。そうすると、逆に上下のプロセッサがそれぞれの横の領域と
自分の領域の相互作用を計算してくれるので、その分は計算しなくても合計さ
れた力が帰ってきます。横の領域は対称性を使えば4個だけでよいので、
結局6個の領域から粒子をもらってくればすむはずです。元々の13個に
比べると半分以下です。さらに、プロセッサ数を8倍にした時には、
もらってくる必要がある領域は16個で、元々の124 個に比べると 1/8 になる
わけです。
漸近的には、プロセッサ数の大きな極限で元々の方法だとプロセッサ当りの通
信量がプロセッサ数に依存しなくなるのに対して、変更後の方法だとプロセッ
サ数の 1/3 乗に比例して小さくなります。いいかたを変えると、プロセッサ
数の 2/3 乗に比例して必要な通信速度が大きくなるわけです。
これはそんなに大きな効果ではな
いようにもみえますが、そうはいってもプロセッサ数が100倍違うと5倍違うわ
けで、結構大きな効果になります。
まあ、そうはいっても通信は多いわけで、もっと減らす方法はないか、
というのが今日のテーマです。
遠距離力の場合には、粒子数を固定してプロセッサ数を4倍にした時に、通信速
度への要求は2倍にしかならないアルゴリズムが知られています。プロセッサ数
の平方根でしか必要な通信速度が増えないわけです。これは似鳥君によって実
用的なものに改良され、 Cray XT4 で 1万コアを超えるようなところで6万粒子
程度で性能がでることを実証しています。
この方法の原理は、プロセッサを2次元の格子状に配置して、粒子を1方向のプ
ロセッサの数に分割し、プロセッサ (i,j) はグループ i とグループ j の粒
子の相互作用を計算する、というふうにすることです。対称性を利用するなら
2次元格子状といってもたとえ下半分の3角形だけプロセッサをおけばよくて、
最初に対角線の位置のプロセッサ (i,i) がグループ i の粒子をもっていれば、
それぞれが縦及び横に放送し、それから全プロセッサが相互作用計算し、計算
した相互作用をまた縦横に合計すれば対角線上のプロセッサに合計の力が求ま
ります。
近距離力の場合に同じことをすることを考えてみます。最初の話のように限界
距離の領域分割をしたとして、領域数の2乗のプロセッサを用意すれば遠距離力
の場合と同じように近距離力も計算できますが、近距離力なので計算が発生す
るのは対角要素以外のところは縦、横ともに13個しか要素がない疎行列の形に
なります。なので、これらの、計算する必要があるところ以外のプロセッサを
全部とっぱらってしまえば、必要なプロセッサ数は領域数の14倍ですみます。
この時に、対角プロセッサの通信量を考えると、縦横に放送して結果が帰って
くるだけなので領域2個分ですんで、 Anton で使われているアルゴリズムに比
べてさらに半分です。ここでは 14 倍の数のプロセッサを使っていま
すから、計算量は 1/14 になってしまっていて、 Anton でプロセッサ数を14
倍にすれば通信量はやはり 1/2 程度になってあまり変わらないともいえます。
ここで、領域の1辺を 1/2 にした場合を考えます。そうすると。通信量は 1/8
になるのに対して、計算量は、プロセッサ数が 64 倍になるので 1/64 です。
従って、遠距離相互作用の場合と同じく、必要な通信速度がプロセッサ数の平
方根でしか増大しない、ということになり、 Anton の方法の 2/3 乗に比べてさ
らに良いスケーリングとなっています。
(ここから2010/1/16 追記)
と、書いたら Anton 関係の論文をちゃんと読んで
なかったのがばれて似鳥君の twitter で嘘なところを指摘されました。
プロセッサ数を 8 倍でなくて16倍にすることを考えて、z方向だけ 1/4 にす
るんだそうで、そうすると通信量は 1/4 になってプロセッサ数の平方根に
なり、スケーリングは同じです。通信量がプロセッサ数の平方根というのは
おそらく原理的な限界だと思うので、スケーリングという意味では同じです。
Anton の方法(NT法)で、単純な分割だと z 方向の通信が xy 方向よりも少な
いので、z 方向を増やすことで xy 方向を減らすことができれば得になります。
そのためには、領域を z 方向に薄いものにするべきなわけです。
というわけでスケーリングは同じなので、係数がどうか?というところです。
どちらの方法でも、相互作用計算は基本的に全部、外からデータをもらってき
て相互作用を計算し、結果を全部外に送り出す、ということになります。なの
で、通信量自体は同じです。実際に、それぞれが多数の領域を担当す
る(多数のプロセッサをもつ)複数のチップからなるシステムを考えた時に
どうなるか、を考えても、まあ、あんまり変わらないです。
ハードウェア設計の手間は、 NT 法に比べて上の方法のほうが小さくはなりま
す。通信が固定パターンでの放送と総和だけなので、それ専用のハードワイヤ
ドなネットワークでよいからです。NT 法では、効率を上げる、つまり通信レイ
テンシを下げるには3次元トーラスの中で結構フレキシブルに通信制御を行う必
要があります。かなり複雑なルーティングと、ルーティングしながらの加算を
行うからです。
(ここまで2010/1/16 追記)
まあ、上に述べた方法の問題というか未解決なところは、ネットワークのトポ
ロジ自体が領域サイズと限界距離の比に依存する、ということです。但し、限
界距離は、分子間力なら定数ですが、クーロン力を PME (P3M) でやるなら変数
であり、そっちのほうが限界距離が大きいのが普通なので、PM のほうを調整す
ればよい、というところはあります。
Anton では
まあ、これについては、今考えたのは前のステップとの密度分布の差分をとっ
て、それを低精度の FFT で評価する、という方法です。1ステップが 1fs く
らいだとすると、原子は 1 pm くらい動く計算です。これに対して、シミュレー
ションボックスは 10nm とかの程度ですから、
密度場については時間の高階差分から予測子を構成するようにすれば、予測子
の精度に応じて必要な FFT の精度を下げることができるはずです。例えば、
3ステップの予測子ならおそらく3桁程度の精度があるので、 FFT の精度はさ
らに3桁下げることができて 2-3 ビットですむはずです。こうなると、
通信速度が 10GB/s、演算速度が 2-3bit の演算で Tops ということになって
今の FPGA 1つでもできる程度です。丸め誤差の累積が気になりますが、
これは時々諦めて高い精度で FFT をすればよいでしょう。
ここでの予測は FFT の必要精度を下げるだけなので、時間積分の安定性や長
時間誤差には影響しないはずです。まあ、適当な実装を作って精度評価してみ
る必要はあります。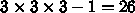 個のプロセッサから粒子をもらってくる
必要があります。作用・反作用の法則を使うなら、もらってくるのは半分の13
個のプロセッサからにして、計算した力を送り返すようにすれば通信量はあま
り減らないですが計算量は半分になります。
個のプロセッサから粒子をもらってくる
必要があります。作用・反作用の法則を使うなら、もらってくるのは半分の13
個のプロセッサからにして、計算した力を送り返すようにすれば通信量はあま
り減らないですが計算量は半分になります。
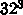 の FFT を数マイクロ秒でやっています。1メッシュあた
りの演算を 150 とすれば、これはテラフロップス程度で演算速度は大したこ
とはありません。問題は例によって通信です。データ量は単精度とすれば128
kB ですが、これをマイクロ秒で通信するには 128GB/s の転送速度が必要なわ
けです。
の FFT を数マイクロ秒でやっています。1メッシュあた
りの演算を 150 とすれば、これはテラフロップス程度で演算速度は大したこ
とはありません。問題は例によって通信です。データ量は単精度とすれば128
kB ですが、これをマイクロ秒で通信するには 128GB/s の転送速度が必要なわ
けです。
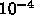 程度、メッシュ
サイズに比べて 1/300 程度、カットオフ波長に比べると 1/1000 以下です。
なので、まあ 10ビットも精度があればいいと思うと、固定小数点なら通信が
1/3 ですが、まだそれほど嬉しいわけではないですね。
程度、メッシュ
サイズに比べて 1/300 程度、カットオフ波長に比べると 1/1000 以下です。
なので、まあ 10ビットも精度があればいいと思うと、固定小数点なら通信が
1/3 ですが、まだそれほど嬉しいわけではないですね。