アムダールの法則は、並列計算の効率についての法則と思って使う人が多いで
すが、ムーアの法則と並んで誤用が多いものです。元々のアムダールの論文で
は、主張されていることはあるプログラムのうち x の部分を P 倍速く実行す
るけど残りの (1-x) のところはそのまま、という計算機を作ったとすると、
プログラムの実行速度はもとの計算機に比べて 1/(1-x+x/P) 倍であり、 P が
無限大であっても 1/(1-x) である、というものです。
これは、まあ、 30年くらい前にベクトルプロセッサとかの議論をする時にはそ
れなりに意味があったし、現在でも、例えば SSE 命令や AVX 拡張のような、
命令セットの拡張、あるいは OpenMP やスレッド並列のような共有メモリ並列
化の効率を議論する際には十分に意義があります。
しかし、近年の、例えば MPI で大規模並列化されたアプリケーションでは、
並列プログラムの実行時間は上の 1-x+x/P という簡単なモデルで表すことは
できません。理由は簡単で、このモデルには通信時間というものがはいってい
ないからです。元々のプログラムが1プロセッサで動いていたなら、もちろん
通信は起きないわけですが、分散メモリで複数プロセッサになった瞬間に必ず
通信が発生します。なので、実行時間は、例えば
というような感じになります。ここで 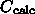 は1プロセッサの時
の計算時間で、計算時間は理想的に並列化されてプロセッサ数
は1プロセッサの時
の計算時間で、計算時間は理想的に並列化されてプロセッサ数 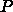 に反比
例して減るものとします。つまり、アムダールの法則はすでに無視しています。
これでよいのは、ある程度まともに並列化されたアルゴリズムやプログラムな
ら既に並列化されていない部分の寄与なんてものは殆どなく、逆にそんなもの
があっては例えば 1000 プロセッサとかで効率良く動くはずがないからです。
に反比
例して減るものとします。つまり、アムダールの法則はすでに無視しています。
これでよいのは、ある程度まともに並列化されたアルゴリズムやプログラムな
ら既に並列化されていない部分の寄与なんてものは殆どなく、逆にそんなもの
があっては例えば 1000 プロセッサとかで効率良く動くはずがないからです。
 は通信時間の定数で、
は通信時間の定数で、
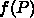 は通信時間がプロセッサ数
は通信時間がプロセッサ数 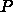 によってどう変わるかを示す関数
です。
によってどう変わるかを示す関数
です。
ここで問題なのは、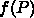 の形がアルゴリズムを決めないと決まらない、
ということです。例えば、3次元メッシュを規則的に分割して、境界メッシュ
を隣と通信するようなアプリケーションなら
の形がアルゴリズムを決めないと決まらない、
ということです。例えば、3次元メッシュを規則的に分割して、境界メッシュ
を隣と通信するようなアプリケーションなら
というような感じになります。 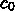 は通信レイテンシによる定数で、第2
項が通信量に比例する成分です。この場合には、実行時間の下限がでるので
アムダールの法則的な議論ができないわけではないですが、問題は、その
形の議論では暗黙にいわゆる強いスケーリング (strong scaling) が前提になることです。ここで
強いスケーリングとは、問題のサイズを変えないでプロセッサ数を変えた時の
計算時間がどうなるか、というものです。
は通信レイテンシによる定数で、第2
項が通信量に比例する成分です。この場合には、実行時間の下限がでるので
アムダールの法則的な議論ができないわけではないですが、問題は、その
形の議論では暗黙にいわゆる強いスケーリング (strong scaling) が前提になることです。ここで
強いスケーリングとは、問題のサイズを変えないでプロセッサ数を変えた時の
計算時間がどうなるか、というものです。
速い計算機を使う目的の結構な部分が、遅い計算機ではできなかった大きな問
題を解く、ということですから、あるアルゴリズムや並列計算機が現実的かど
うかを調べるには、現実的な時間で解けるような問題サイズに対して並列性能
がどうなるか、を調べないと意味がないように思われます。この点の改善のた
めに導入されたのが弱いスケーリング(weak scaling) ですが、これは、「プロ
セッサ当りの問題サイズ」を一定にした時の効率、となります。上の、メッシュ
の例だと、 OS のジッタとかで通信時間がばらつくとかそういう細かい話を無
視すると、この時の実行時間は 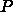 に無関係になるので、並列化効率も一定、
となるわけです。
に無関係になるので、並列化効率も一定、
となるわけです。
この、弱いスケーリングにはまた大きな概念上の問題があります。単純にプロ
セッサ当りの問題サイズを一定にしたら、サイズが大きな問題が実際に実用的
な時間で終わるかどうかはわからないからです。例えば、球状星団の N 体計算
では計算量は 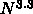 程度ですから、 P を N に比例させると計算時間が
程度ですから、 P を N に比例させると計算時間が
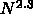 に比例して増えてしまって全く話になりません。
に比例して増えてしまって全く話になりません。
意味がある議論をするためには、問題サイズではなくて計算時間一定のスケー
リング、つまり、 N を変えた時に、 P をいくつにすればその時間で計算が終
わるか、あるいは、 P を変えたら実際にどれだけ大きな計算ができるか、と
いうことを問題にしないといけないわけです。ここでは、このようなスケーリ
ングを実行時間一定スケーリング (constant execution time scaling) と呼
ぶことにしましょう。数式としては、これは以下のように表現されます。
まあ、みての通り、 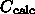 とかが N の関数になっただけです。
未知関数が 3個もあるので全く意味不明ですが、2ー3個例をもってきて考えて
みます。
とかが N の関数になっただけです。
未知関数が 3個もあるので全く意味不明ですが、2ー3個例をもってきて考えて
みます。
まず、メッシュ計算の場合です。タイムステップが、例えば CFL 条
件で決まっているとすれば、計算量はメッシュ数の 4/3 乗です。今簡単のた
めに通信レイテンシを無視すれば、計算のところは 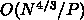 で、
通信は
で、
通信は 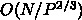 となるわけです。なので、計算時間を一定にしてみ
ると、
となるわけです。なので、計算時間を一定にしてみ
ると、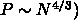 となって、通信時間は
となって、通信時間は 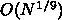 となり、
段々通信時間の割合が増えることがわかります。レイテンシの寄与は
となり、
段々通信時間の割合が増えることがわかります。レイテンシの寄与は
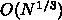 なので、こちらのほうがよりきつい制限になる可能性が高いで
す。
なので、こちらのほうがよりきつい制限になる可能性が高いで
す。
HPL ではどうでしょう?計算のところは 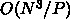 で、通信は
で、通信は
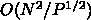 ですから、もしも計算時間一定にしようとしたとすると
通信時間が
ですから、もしも計算時間一定にしようとしたとすると
通信時間が  になってしまい、実は流体計算等よりはるかに
厳しい問題である、ということがわかります。現在、 HPL で多くの計算機で
ピークに近い性能がでるのは、メモリ一杯のサイズの計算機にすることで、
大きな計算機では無制限に実行時間が伸びることを許しているからにすぎませ
ん。例えば、 1時間以内に計算を終える、という条件をつけるだけで HPL は
現在よりはるかに通信負荷の高いベンチマークにできることがわかります。
になってしまい、実は流体計算等よりはるかに
厳しい問題である、ということがわかります。現在、 HPL で多くの計算機で
ピークに近い性能がでるのは、メモリ一杯のサイズの計算機にすることで、
大きな計算機では無制限に実行時間が伸びることを許しているからにすぎませ
ん。例えば、 1時間以内に計算を終える、という条件をつけるだけで HPL は
現在よりはるかに通信負荷の高いベンチマークにできることがわかります。
通信時間一定のスケーリングは 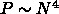 なので、レイテンシが無視で
きる範囲では計算機のサイズが大きくなればできる問題のサイズも大きくはな
ります。が、通信がリミットするようになると実行効率は N に反比例して
落ちるようになるわけです。まあ、これでは厳し過ぎる、というのが逆に
問題になりそうですね。
なので、レイテンシが無視で
きる範囲では計算機のサイズが大きくなればできる問題のサイズも大きくはな
ります。が、通信がリミットするようになると実行効率は N に反比例して
落ちるようになるわけです。まあ、これでは厳し過ぎる、というのが逆に
問題になりそうですね。
ついでなので球状星団の場合です。アルゴリズムとして似鳥君の Ninja を想定
して、理想的に動いたとしましょう、そうすると、計算のところは
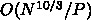 で、通信は
で、通信は 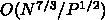 です。
です。
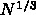 を除いて HPL と同じスケーリングになっていることがわかりま
す。まあ、現実問題としては球状星団の計算の場合にはレイテンシがもっと強
くきき、楽観的にみても
を除いて HPL と同じスケーリングになっていることがわかりま
す。まあ、現実問題としては球状星団の計算の場合にはレイテンシがもっと強
くきき、楽観的にみても 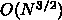 程度になるために通信レイテンシを引
き下げないと大きな計算は実行不可能です。
程度になるために通信レイテンシを引
き下げないと大きな計算は実行不可能です。
さらに、宇宙論的シミュレーションの場合を考えてみます。タイムステップの
スケーリングは良くわからないですが、 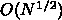 としてみましょう。
そうすると、
としてみましょう。
そうすると、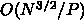 で、通信は
で、通信は 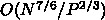 です。
計算時間一定では通信が
です。
計算時間一定では通信が 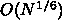 となるわけです。
となるわけです。
上の例から一般的なことをいうのは無理がありますが、それでも無理に少しい
うと、以下のようなことがいえます。
プロセッサ速度一定、計算時間一定のスケーリングでは、プロセッサ数を増や
すと
-
プロセッサ当りの必要メモリはプロセッサ数の弱いべきで減り
-
プロセッサ当りの必要通信バンド幅はプロセッサ数の弱いべきで増える
今後コアのクロックがあがるわけではないですが、ノード当りのコア数は増え
るわけです。そうすると、上のが少し変わって
-
演算速度があがるほどにはメモリは増えなくてもよい
-
ノード当りの通信バンド幅は結構増えないといけない
ということになります。少しわかりにくいですが、3次元流体計算の場合に
これをみてみましょう。今までとは逆に、ノード数が一定で1ノードの計算速
度が速くなった場合に、通信時間はどうなるかを考えます。これは、
計算は 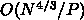 で、通信は
で、通信は 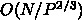 でした。
今、計算速度を
でした。
今、計算速度を  倍にすると、同じ時間で
倍にすると、同じ時間で 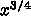 だけ大きな
計算ができます。通信を同じ時間でおわらせるためには
だけ大きな
計算ができます。通信を同じ時間でおわらせるためには 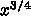 だけ速
くないといけません。つまり、
P が一定の時には従って通信速度は計算速度の 3/4 乗と、非常にきついべき
で増えないといけない、ということがわかります。HPL、球状星団、
宇宙論ではそれぞれ、 2/3、7/10、7/9 となって、アプリケーションによらず
に 2/3 から 4/5 程度の狭い範囲にきます。
だけ速
くないといけません。つまり、
P が一定の時には従って通信速度は計算速度の 3/4 乗と、非常にきついべき
で増えないといけない、ということがわかります。HPL、球状星団、
宇宙論ではそれぞれ、 2/3、7/10、7/9 となって、アプリケーションによらず
に 2/3 から 4/5 程度の狭い範囲にきます。
まあ、べきが同じ、というだけで係数はアプリケーションで全然違うのですが、
しかし、一般論としてはこれは極めて深刻な問題で、マルチコア・メニーコア
当で計算機の1ノードが速くなった時に、ノード間通信速度は比例までいかない
にしても最低 2/3 乗程度で大きくなっていく必要がある、ということです。
ここで問題になるのは主に電力です。3次元トーラスのような、もっとも配線が
短くてトランシーバーのドライブ能力が少なくて良いネットワークを考えても、
半導体の集積度が上がったからといって転送速度あたりの消費電力を減らすの
は容易ではないからです。ケーブルの特性インピーダンスをドライブする必要
がどうしてもあります。まあ、 LVDS だとドライバ自体は 0.1 W 程度で
10Gbps くらいをなんとかできるようなので、 1Tbps 程度まではそれほど深刻
ではありませんが、しかし、1チップで 10Tflops はもう手の届くところですか
ら、そうなると通信速度は 1Tbps 弱が必要になり、そろそろ無理になってきま
す。それ以前に、ノード内で PCIe に出してさらに IB のインターフェースチッ
プにいれて、さらにそれを光に変換、とかすると電力消費がすぐにオーダーで
上がってしまい、全く話になりません。つまり、近い将来の並列計算機では、
計算ノードの CPU チップ自体に、通信ケーブルのドライバまで含んで通信イン
ターフェースを集積するのが必須ということになります。前回は、レイテンシ
の面からネットワークインターフェースは集積しないと、と書いたわけですが、
バンド幅、消費電力の観点からも同じ、ということです。
ネットワークはもちろん結局は主記憶にデータがいかないといけないので、ネッ
トワークインターフェースがあるチップと主記憶インターフェースがあるチッ
プは物理的に同じでないとそこの間で消費電力やレイテンシの問題が発生しま
す。これはつまり、こういう状態になるとアクセラレータと CPU とネットワー
クインターフェースがそれぞれ別チップ、というような構成はもう駄目で、全
部集積しないといけない、ということです。 OS を走らせるのに x86 があって
もよいですが、演算を別チップがするならx86 側の主記憶インターフェースに
データがあってはもう駄目で、別チップ側にメモリインターフェースとネット
ワークインターフェースを置く必要があります。
まあ、プログラミングモデルとしては、 x86 側から別チップ側のメモリが見え
ればよいわけですが、これはそうすると PCIe の向こう側のデバイスメモリを
キャッシュコヒーレントな空間に置くとか、そういう話になってあまり簡単で
はありません。フレームバッファみたいに書くだけでよければWC (write
combining) な空間に置けばよくて、それは普通にやってるのですが、問題は読
出しです。今は亡き DEC Alpha のPCI バスのインターフェースには、 read
combinig というべき機能があって、連続アドレスのリーダーがバーストリード
に変換されて結構なパフォーマンスがでたのですが、 Intel はそういうのは嫌
いなのか、 PIO read で性能がでる x86 用チップセットというのはみたことが
ありません。というか、Alpha と K7 で共通に使えた AMD750 でも Alpha でな
いと PIO read も write もバーストで動かなかったし。
原理的には PIO read のレイテンシがいくら大きくても、 outstanding read
を発行できるならキャッシュできるようにしてやればよいはずではありますが、
まあ、少なくとも Intel x86 プロセッサにそんなことを期待しても無理です。
AMD の場合には ccHT ならもちろんそういうのができるわけですが、コヒーレ
ンシをとるならもちろんバススヌープのためにデータを送る必要があるので
別チップ側のメモリアップデートを全て通信バスに流す必要があると
いうことになってなんだか具合がよくありません。
これは、GPGPU みたいなものをキャッシュコヒーレントにできるか、というの
と同じことですが、GPGPU 側のメモリバンド幅が非常に大きいとすると、ディ
レクトリキャッシュにしていない限りキャッシュラインのインバリデートだけ
でものすごい量のトラフィックが発生してしまいます。これは普通の共有メモ
リマルチソケットのサーバーで 16コアくらいからも破綻する、というのと同じ
話で、キャッシュがあると他のコアのメモリアクセスの情報が全部あるコアに
こないといけなくなって、性能がでなくなるわけです。Barcelona でのマルチ
ソケットの AMD サーバーではメモリバンド幅等に結構深刻な問題があったのは
これが原因でした。
ハードウェア的に、アクセラレータ側のメモリを x86 側から普通のメモリで
あるかのように、低レイテンシでしかも高速にアクセスできるようにする
汎用的な方法、というのはなかなかないような気がします。