スーパーコンピュータを、大規模な数値計算、つまり、小規模な独立な問題を
沢山並列に解くのではなくて一つの問題、例えば地球全体の気候とか、あるい
は宇宙の大規模構造とかをなるべく高い空間分解能で計算する、といった問題
に使うことを考えてみると、それにはどのような形でプログラムを書くのがハー
ドウェア、ソフトウェアの観点から見てよいということになるでしょうか?
1970年代から 80年代にかけて日本で独自の並列計算機を開発していた川合先
生、星野先生達は、このような大規模シミュレーションを3種類に分類してい
ます。
-
近接型
-
遠隔型
-
不規則型
近接型とは、基本的に偏微分方程式の離散近似によってでてくるものです。つ
まり、例えば流体力学であれば方程式はナビエ・ストークス方程式で、空間の
各点での流体の速度変化、つまり時間微分がその点での圧力や速度等の空間勾
配、つまり空間微分の関数で与えられています。
離散近似では、例えば空間1次元であれば空間座標で等間隔に数値解の値を表
現する点を並べて、それらの点での値から空間微分を計算します。時間方向も、
ある時刻  での値とそこから少したった
での値とそこから少したった 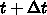 の値、あるいはそ
の前後のいくつかの値を使って時間微分を表現し、それから
の値、あるいはそ
の前後のいくつかの値を使って時間微分を表現し、それから 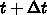 で
の解を求めます。2次元とか3次元では、簡単には他の方向も同様に規則的に切
ります。
で
の解を求めます。2次元とか3次元では、簡単には他の方向も同様に規則的に切
ります。
この場合、数学的な構造としては、離散近似された方程式では空間のある点、
つまりあり格子点での変数の新しい時刻での値は、その点に近いいくつかの
格子点の値から計算できます。
これに対して、遠隔型のもっともわかりやすい例は重力多体問題で、ある一つ
の星は他の全ての星からの重力を受けます。数値計算でも、単純にはある星の
加速度は他の全部の星からの重力を計算して合計することで求めます。
最後の不規則型はこのどちらにもならないようなものです。簡単な例は大規模
な回路、例えばマイクロプロセッサとかのシミュレーションで、あるトランジ
スタは他のいくつかのトランジスタにつながっていますがそのつながり方は設
計によっているわけで物理的に近くのトランジスタがつながっているというわ
けではありません。
星野先生、川合先生は、このような分類をした上で、「直接写像」、つまり、
問題に対して自然な数値解法、自然なハードウェアを使う、ということを提唱
されました。それが PAX の考え方で、近接型の問題には近接結合の計算機を、
というものです。他の問題では違う形がありえるかもしれないけれど、実は近
接結合で結構良い性能がでる、というのも彼らの主張です。
歴史的には、その頃までの多くの並列計算機がもっと複雑なネットワークを使
おうとしていたのに対して、 PAX の非常に単純な2次元ネットワークは研究と
してはあまり面白いものとはみなされなかったようです。しかし、実用上は
そうではなく、例えば Intel iPSC のハイパーキューブ型の計算機は 1990 年
頃に PAX と同様な 2 次元ネットワークに移行します。 Cray の超並列機も初
めから 3 次元ネットワークでした。これは XT3 になって復活をとげています。
しかし、ここで少し注意しないといけないことは、上の分類は一応対象とする
系の性質ではありますが、実は人間の認識の問題でもあり、従って数値計算法
がどうなるかは対象とする系を表す方程式の見かけだけからは決まらない こ
ともある、ということです。
また重力多体問題を考えます。沢山の粒子の間の重力相互作用はもちろん全部
の相互作用を合計することでも計算できますが、それだけが計算方法ではあり
ません。粒子の数が十分多い時には、その粒子全体が作る重力場を考えて、そ
れぞれの粒子はその重力場の中で運動する、と考えることができるからです。
この時は、重力場が満たす方程式はポアソン方程式という空間微分だけの微分
方程式になり、空間格子を切って質量分布を求め、それから重力場を計算する
ことができます。この時には、元々の方程式は遠隔型であったとしても、
それを近接型に書き換えることができたわけです。
このような書き換えまではやらなくても、例えばツリー法や FMM (高速多重極法)
といった速い計算法は、基本的には遠くのほうの粒子からの力はまとめて計算
する、という方法です。この場合には、遠くのほうからの情報はあまり必要で
はなくなるので、元々の方程式の数学的形式は遠隔型であってもプロセッサ間
の結合としては近接型に対応するようなもので十分ということもあります。
逆に、方程式は近接型であっても計算法としては遠隔型的なものが必要になる
ような場合もあります。その典型的な例が高速フーリエ変換を使う計算法です。
フーリエ変換とは、簡単にいうとある関数を沢山の三角関数の合計で表すこと
です。フーリエ展開ともいいます。ある区間で与えられた関数を定数、その区
間が周期の三角関数、周期が区間の半分の三角関数、 1/3 の、、、と無限に
短い周期のものまで使って表すわけです。一旦そのような展開を行うと、例え
ば前にでてきたポアソン方程式を解くのは、密度分布が三角関数なら重力場も
三角関数で、比例係数が周期によるだけなので微妙方程式は解けていて、展開
係数にこの比例係数を掛けてでてきたフーリエ展開を逆変換してやるとポアソ
ン方程式の答がでる、ということになります。
ある一つの波長についてフーリエ展開係数を求めるには、元の関数にその波長
の三角関数を掛けたものを区間全体で積分します。このため、普通にやると
 項目、つまり波長が区間の大きさの
項目、つまり波長が区間の大きさの 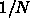 までの展開係数を求める
には
までの展開係数を求める
には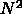 に比例した計算量が必要になりますが、それを上手くやって
に比例した計算量が必要になりますが、それを上手くやって
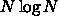 の計算量ですます方法が知られています。これを高速フーリエ変
換、あるいはFFT と呼びます。並列計算することを考えると、これは全結合で
はないのですが、例えば
の計算量ですます方法が知られています。これを高速フーリエ変
換、あるいはFFT と呼びます。並列計算することを考えると、これは全結合で
はないのですが、例えば 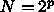 のサイズの FFT を
のサイズの FFT を 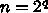
 のプロセッサでやると、各プロセッサは自分と 1,
2, 4 ...
のプロセッサでやると、各プロセッサは自分と 1,
2, 4 ... 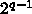 だけ離れたプロセッサと通信する必要がおきます。
だけ離れたプロセッサと通信する必要がおきます。
これは遠隔型かと言われるとそうでもないのですが、プロセッサを 2 次元と
か3次元の格子に並べて隣だけとつないだのでは上手くいかない例になってい
ます。
もっとも、通信がそこそこ速く、ノードプロセッサの台数があまり極端に多く
なければ、 2 次元や3次元の格子でも FFT で結構良い性能を出すことができ
ます。しかし、そのためには結局演算速度と通信速度の比が 1 に近い必要が
あり、例えば 100:1 とか 1000:1 といった構成では使いものになりません。
また、近接型の問題で、実際に FFT でなくて空間微分を計算するものであれ
ば2次元や3次元の規則的なプロセッサ結合でいいかというと、これも必ずしも
そうではありません。工学的な問題で複雑な形状のものを扱うとか、あるいは
必要な精度に応じて空間分割を変えるようなことを考えると、規則的な格子で
はなくて適当な形の三角形や四面体で空間を切る、という方法が具合が良いで
す。この時は、切ってできた点に番号をつけると、点同士がどうつながってい
るかは番号だけからはわからないわけで、不規則型になってしまいます。
もっとも、この場合でも、空間的に近いもの同士しかつながっていない、とい
うのは間違いないので、並列計算を考えると空間をおおむね規則的に分割して、
自分が担当する領域にはいっている点は自分が面倒を見る、という形にすると
プロセッサ間の通信は隣あったプロセッサ同士だけで大体済むことになります。
なんだか話がまとまらないですが、要するにこれは、対象とする問題、数値解
法、ハードウェアの関係は単純ではない、ということです。ある問題に対して
数値解法を決めてしまえば、並列計算をする時にハードウェアにどのような要
求がでるかとか、またどのようにプログラムすれば良いかはほぼ決まります。
しかし、本来はハードウェアをどのように作るかと、数値解法をどうするかは独
立の問題ではなく、両方を同時に変えてなるべくベストに近いやり方を考える
必要があるわけです。
とはいえ、ハードウェアも数値解法も、開発には時間がかかり、現時点で利
用可能なものは過去の歴史をひきずっています。これは、過去の歴史を無視した
ものを開発しようとすると結局歴史を繰り返すだけの時間がかかる、というこ
とでもあります。
まあ、でも、なんかそんなことを言われても良くわかんないですよね?
もうちょっと具体的に考えるため、次章では私達のやってきた重力多体問題専
用計算機の開発の歴史を振り返ってみましょう。