この、NBODY5 というプログラムは多少の変更を経て NBODY6 という名前にな り、2006年の現在も当初からの開発者である Aarseth によって開発、メンテ ナンスが続けられています。 NBODY6 はシングルプロセッサ、あるいは共有メ モリの計算機用であり、分散メモリのシステム用には MPI を使って並列化し た NBODY6++ というプログラムが 90年代中頃からハイデルベルグ大学のグルー プによって開発、メンテナンスが続けられています。このコードは、 NBODY6 の元々のプログラムのほとんどのところは並列化しないで、 MPI で動いてい る全部のノードで重複した計算をします。計算量の多い粒子間の重力の 計算のところだけは並列化する、というアプローチをとることによって並列化 のためのプログラムの変更を最小限にし、上に書いた

  「一度には一ヶ所しか変更しない」

私達は GRAPE という、こういったシミュレーション向けの専用計算機を作る、 と試みを 1989年に始めました。この場合もアプローチは NBODY6++ と同じで、 というか私達のほうが先ですが、計算量の殆どを占める粒子間の重力の計算だ けに自分達で作った専用計算機を使い、それ以外のところは普通の汎用計算機、 最初の頃はワークステーションで今は普通の PC ですが、を使う、そのため計 算コードの 99% は Aarseth が書いたものをそのまま使う、というふうにして きています。また、幸運なことに Aarseth 本人が GRAPE を気にいってくれて、 GRAPE のためのプログラム開発もやってくれています。 その結果、球状星団のシミュレーションについては、最新鋭の GRAPE で初め から Aarseth のプログラムが動く、という状態になっています。

もちろん、このやり方には限界があります。並列計算機にしても GRAPE にし ても、相互作用の計算があまりに速くなると、どんなにその部分の計算量が多 くても、いつかはそれ以外の残りの部分が問題になってしまいます。これは、 良く知られたアムダールの法則というものです。

アムダールの法則とは、ある問題を解くあるプログラムを考えた時に、全体の 計算量を 1 として 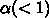の部分だけを 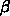倍速くできる ような計算機を考えると、 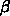がどんなに大きくても計算全体としては 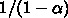倍しか速くならない、というものです。例えば 99\% の部 分を10倍速く計算できたとしたらほとんど10倍速くなりますが、 100倍の時は 全体としては 50倍、1000倍の時でも 90倍にしかならないわけです。

この法則の算数は自明ですが、それが計算機の作り方、使い方にとって何を意 味しているかはそんなに自明ではありません。上は、ある問題を、あるアルゴ リズムで解く、あるプログラムについて、の話であって、例えば問題を変えな くてもアルゴリズムを変えれば話は変わるし、アルゴリズムは同じでもプログ ラムの書き方によって話は変わるし、また、問題自体も見方によっては変わる からです。

1つの例として、重力3体問題を考えてみます。重力3体問題とは、お互いに重 力を及ぼしあう3つの天体がどう運動するか、という問題です。天体が2つの時 には数値計算しなくても答が求まる、というのはニュートンの偉大な業績です が、では3つ以上では、というか、まず3つではどうか？というわけです。

もちろん、例えば太陽系の惑星の運動だって、惑星が複数あるから単純に 2体問題というわけではありません。しかし、この場合にはまずそれぞれの惑 星の運動を太陽からの重力だけを考えて解いておいて、それを基準にしてそれ からのずれの部分を計算する、という方法で、精度良く計算できます。そうい う方法を使って、 ラプラスやラグランジュといった人達は惑星の未来の位置 を精度良く予測することに成功したのです。こういうやり方を摂動法といいま す。

が、そういう方法は、「基本的には2体問題とみなせる」という特別な状況で しか使えません。例えば、地球の質量は太陽の100万分の1、最大の惑星である 木星でも 千分の1です。そういう時には、木星の重力の地球の運動への影響は 小さいので、上に述べたような扱いができます。 しかし、例えば月の運動になると話がややこしくなります。月は地球を回って いるわけですが、太陽は遠いとはいえ大きいのでその影響は大きいですし、ま た地球からも近いので地球が完全な球ではないことの影響も受けます。これら のために、月の軌道を正確に遠い将来まで計算するのは結構難しいことです。

地球に近付く、あるいは衝突するような小惑星や彗星だと、その軌道計算はもっ とややこしくなって、基本的には計算機で数値計算するしかなくなります。ま た、惑星の軌道でも、非常に遠い将来のことまでを考えると、上で述べた摂動 法が正しい答を出すかどうかが問題になって、数値計算も必要になってきます。 これらの問題では、天体3個とか、太陽系全体でも 10個とかの非常に小さい系 の計算をする必要があります。これは並列計算機には普通に考えるとあまり向 いていません。

並列計算機の考え方は、要するに沢山の計算機をつないで、それらで分担でき るような仕事があれば分担することで早く終わらせよう、というものです。 例えば3体問題の数値計算では、普通の計算機では以下のような手順で計 算します。

    最初の天体の位置、速度を決める。
    以下を繰り返す。
        天体同士の重力を計算する
        求まった重力を使って、少し先の時刻での天体の位置、速度を計算する
        計算終わってよければ終わる。そうでなければ繰り返しに戻る

しかし、現実問題としてはだから 3 体問題を例えば 9 台の計算機で並列処理 できるかというと、そうはいかないのが現状です。これは、作業を分担するに は計算機同士がデータをやりとりする必要があるのに、それには結構時間がか かるからです。

例えば、今のマイクロプロセッサは 3GHz 程度のクロックで動いていて、クロッ ク毎に 2 ないし4演算します。つまり、大雑把にいって 100ピコ秒に1演算し ているわけです。ところが、計算機同士を例えば普通のギガビット・イーサネッ ト(GbE)でつないだとすると、一方の計算機がデータを送りはじめてから他方 に実際にデータが届くまでには大体 30マイクロ秒かかります。 GbE のハード ウェアはそのまま使っても、ソフトウェアを書き直して早くすればこれが5マ イクロ秒くらいになりますし、高価なインフィニバンド (IB) や QSNet といっ たものを使えばさらに 1マイクロ秒くらいまでこの時間を短くすることも可能 です。しかし、それでも100ピコ秒と比べると1万倍という全く話にならないほ どの違いがあります。 このために、普通のやり方で 3 体問題を解く時には、 普通の並列計算機を使うというのは現実的ではありません。

普通でないやり方で計算するか、あるいは普通ではない並列計算機を使えば、 なにかできないとも限りません。スーパーコンピュータのソフトウェア、ハー ドウェアの開発とは要するにそういうことなわけです。

ソフトウェアのほうですが、最も極端な、しかし極めて有効なアプローチは、 沢山の3体問題を並列に解く、ということです。多くの場合、3体問題を計算機 で解くのは、1つだけ計算しておしまい、というわけではありません。という より、そういう場合ももちろんありますが、その時には最近の速い計算機なら 並列計算するまでもなく計算がおわってしまうので、あまり難しいことを考え る必要はありません。沢山計算機を使って並列計算までして速度を上げたいの はそもそも沢山の3体問題を解きたいからだったりします。

何故そのようなことをしたいか、ですが、これには色々な例があります。私達 がやった割合最近の研究では、カイパーベルト天体の連星がどのようにして出 来たものかをシミュレーションで調べる、というものがあります。

こういったところでシミュレーションで調べるというのは、多くの場合に「こ ういうふうにできたとしたらいろんなことが上手く説明できるのではないか」 という理論というかシナリオというか、そういうものを考えて、それで本当に 上手くいくのかどうかをシミュレーションで調べるわけです。

この研究の場合には、説明したいことは以下のような観測事実でした

• カイパーベルトで見つかっている連星は、2つの天体の大きさがあまり変わ らない。これに対して小惑星の場合は連星というよりは主天体と衛星で、大 きさが全く違う。

• 軌道も、カイパーベルト天体は2つがかなり離れているが、小惑星は非常に近い。

• 離心率(軌道がどれくらい楕円になっているか)も、カイパーベルトでは大きい。

ここで私達の考えたシナリオは、小惑星であるような質量比の大きな連星系、 というか天体と衛星からなる系が、もうひとつの天体と近接遭遇して、その結 果小さな衛星のほうがはじき飛ばされて大きな2つが連星になる、というもの です。実際にそういうことが起こりそうかどうかを調べるために、衛星をもつ カイパーベルト天体ともうひとつの天体の近接遭遇を、軌道を変えて何百万、 何千万というケースについて調べることで、どういうものができそうかを調べ ました。この場合には、3体問題を何千万個も解くわけです。こういった場合 には非常に沢山の計算機で並列処理することができます。

まあ、この場合には実際は研究室にある数台のパソコンで分散処理して数日で 終わったたくらいなのですが、一杯使えたらもっと早く終わらせることはもち ろんできたはずです。このような、1つ1つはそれほど時間がかかるわけではな いけど、同じようなことを非常に沢山やる必要があり、しかもそれぞれは別々 にやっていい、というような問題は計算機の応用としては結構色々あります。

こういうのを並列計算、というとなんか詐欺のような気もしますが、実際には 非常に有用な応用になっているわけです。こういう場合には、先程述べた計算 と通信で1万倍速度が違う、ということも全く問題ではなく、もっと大きな差 があってもかまいません。また、この方法は、実は並列計算機に限らず、ベク トル計算機やあるいは普通の PC の場合でも有効です。というのは、例えば SSE 命令を使うと1命令で2演算されるわけですが、それを最も有効に使う方法 は2つの3体問題を同時に解くことだからです。ベクトル命令でも、ベクトルの 要素数だけの3体問題を並列に解くというのは効率の良い方法です。

1つの3体問題の数値計算自体を並列に計算するような方法も色々研究はされて います。が、頑張っても数倍で、例えば1000台の計算機で1つの3体問題を効率 良く解く方法なんてものは今のところありません。これに対して、3体問題が 1000体とか 1万体とか 100万体問題になれば、沢山の計算機を使って1つの問 題を解く、というのが現実的に意味がある話になってきます。そういうわけで、 この節の初めに述べたような、すでにあるプログラムの一部の変更である程度 の並列処理は可能になります。また、 GRAPE のような専用計算機で計算量が 最も多いところだけを速くする、といったこともできるわけです。

しかし、非常に並列性が高い計算機が使えるとか、あるいは GRAPE のほうが 非常に速くなるとかいったことが起こると、アムダールの法則によってまだ並 列化とか GRAPE で実行とかができていないところが計算時間を使うことになっ てしまい、それを解決するためには簡単なプログラムの変更ではすまず、大が かりなプログラムの書き換えが必要なのが現状です。

何故そのような大がかりな書き換えが必要なのか、ということを次回には整理 してみます。

Previous

ToC

Next