1ノードとして見ると、最近の安価な PC (6-8GB/s) に比べて100倍程度のメモ リバンド幅があります。 しかし、 PC はインターリーブしないでこの速度を 実現しているわけなので、 4096 ウェイは転送速度に対して 2 桁近く高いも のになっています。 その理由は、ランダムアクセスの性能が下がらないよう にしているためです。

実際、 SX-8 ではメモリアクセスの単位は 8 バイトワードであって、普通の PC のように 32 バイトや 64 バイトのキャッシュライン単位というわけでは ありません。アクセスレイテンシの大きなDRAM で小さな単位でのアクセスを 可能にするために極度に大きな数のインターリーブをしているのです。

この構造にすることで

1. memory-to-memory に近い、局所性がないプログラムでも高い実行性能がでる。
2. さらに、ストライドアクセスやランダムアクセスでも高い性能を維持できる。
3. さらに、8 CPU までなら自動ベクトル化(並列化)で高い性能がでる。

4. 複数ノードの並列化も通信がそこそこ高速でネットワークトポロジを考える必要がないので比較的単純なアルゴリズムでも高い性能がでる。

つまり、高価になっている要因はそのまま(従来のベクトル機ユーザーには)使 いやすいものにする要因になっているわけです。

仮にメモリアクセスの単位を 32 バイトや 64 バイトにしたら、アドレスや制 御情報のためのバンド幅が大きく減るのでモジュール間配線を大きく減らすこ とができます。さらにメモリモジュールの構造自体を単純化できるので 大きくコストダウンすることが可能になります。また、 8 CPU チップが物理 的にメモリ共有するアーキテクチャをやめてしまえば、配線の数が 1/8 にな り、さらに短くできるのでもっと高速動作可能とすればさらに本数を減らし、 消費電力も減らすことができます。 ネットワークも、単段クロスバーをやめ て Fat tree やメッシュにすれば 1/10 程度のコストになるでしょう。

このように、アーキテクチャとして問題点ばかりに見える SX-8 ですが、では、 何故そのようなものが作られ、実際にある程度のマーケットを得ているのでしょ うか？作っている/使っている人が保守的だからとか無能だからとかいう理由 をつけてわかったつもりになるのは簡単なことですが、そのような理解で本当 によいかということはちゃんと考える必要があります。

そもそも何故ベクトルアーキテクチャというものが考えられたか？というのを、 現在の時点から振り返ってみることにしましょう。

Semour Cray がベクトル演算を採用したのは、 CDC 8600 の開発を断念した後 のことと思われます。いくつかの証言によれば、 8600 はベクトルレジスタを もっていなかったようです。この頃に CDC では STAR-100 (のちに Cyber-203/205となる) の開発が 進んでおり、また最初の商用ベクトル計算機である TI ASC は既に完成してい たものと思われます。もちろん、 SIMD 並列計算機として歴史的に重要な Illiac-IV の開発も進行中でした。

Cray-1 のベクトルアーキテクチャの特徴は、 6600/7600 に比べた単純さにあります。 6600 は多数の演算器を持ちその依存関係をスコアボードによって制御する 極めて複雑なプロセッサでした。 7600 ではさらにメモリが 2 階層になり複 雑さを増しています。

Cray-1 のベクトルアーキテクチャはこれに比べて極めて単純なものです(スカ ラ部分は結構複雑なものですが)。演算器は乗算、加減算1つづつ、演算命令は ベクトルレジスタ間のみ、メモリとベクトルレジスタ間の転送は連続アドレス か一定ストライドのみ(間接アクセスなし)、といったものです。これは、 ASC や Star の複雑な命令セットとは大きく違うものでした。 ASC, Star ともに ベクタレジスタはなく、メモリからベクトルを読んで直接計算してメモリに返す、 いわゆる memory-to-memory のアーキテクチャになっていました。 ASC では さらに 3 重まで(多分)のループを1命令で実行するという今となっては信じら れないような命令セットをもっていました。

さて、何故ベクトル命令か、ということを考えてみます。これは、少なくとも当時の計 算機アーキテクチャでは、演算器を 100% 有効に使う、ということがそれほど 簡単ではなかったためと思います。 つまり、以下のような単純な fortran ルー プ

   do i=1,n
     c(i) = a(i)+b(i)
   enddo

• a(i) のアドレスを計算する
• ロード命令を出す
• b(i) のアドレスを計算する
• ロード命令を出す
• 加算する
• c(i) のアドレスを計算する
• ストア命令を出す
• インデックス i をインクリメントする
• ループ終了判定をして、おわってなければ前に戻る

これに対して、ベクトル命令にしてしまえば、アドレス加算等はそれ専用の回路 をおけば済むので非常に小規模で高速動作可能な制御回路が実現できます。こ れはメモリ演算の場合でもそうですが、レジスタ演算の場合には一層単純にな ります。もちろん、ベクトルレジスタにかなりのハードウェア資源を投入する ことになりますが、浮動小数点演算器に比べて大きいというほどではありませ ん。

つまり、ベクトルアーキテクチャというのは、考案された当初においては、規 模が小さいハードウェアでなるべく高速な演算器を有効に使うための工夫であっ た、ということができます。

Cray-1 のベクトル命令セットは既に述べたように極めて単純なものでしたが、 X-MP になって複雑化しました。これは

• 2ロード、1ストアの並列実行
• 間接アドレスによるロード/ストア
• マルチプロセッサ

最初の2つはユーザーから見た使いやすさという観点では極めて重要なもので したが、これらにどの程度のハードウェア資源をさくかは難しい問題だったこ とでしょう。実際、日本のベクトル計算機では、ロード/ストアを演算に対し て増やす方向にはいっていません。これは、日本のベクトル計算機では最初か ら Cyber 205 のような複数の演算パイプラインが並列動作するアーキテクチャ をとったことが大きいと思われます。演算パイプライン毎にロード/ストアパ イプラインを複数サポートするのはハードウェア規模から困難だったのでしょ う。しかし、間接アドレスに対しては十分なサポートがあるのが普通であり、 多くのマシンで連続アクセスと間接アドレスアクセスで同じ速度がでるように しています。 これは、内側が短い 2 重ループを間接アクセスによって展開し て1重化し、ベクトル命令1つで実行した時に性能が落ちない、というメリット はあり、比較的ベクトル命令の開始オーバーヘッドが大きい傾向にあるマシン では大きな性能向上につながったと思われます。

もちろん、早い時期からベクトル化コンパイラが前提であった日本の機械では、 Cray と違ってアセンブラで書かれたレジスタ利用効率の低いコードの性能を 考える必要がなく、その分メモリバンド幅を節約出来たということはあるでしょ う。

Cray-1 ではさすがに集積回路を使ったわけですが、これは 4 ゲート のもので1ビットの全加算器も収まりきらないものでした。従って、浮動小数点演算器は 膨大な数の集積回路を配線して作ったわけです。加算器が数千個必要ですから、 配線は数万本になるわけです。メモリチップも数千個あり、プロセッサとメモ リの間を数千本の配線でつないでも、それは全体コストにそんなに大した影響 はなかったでしょう。従って、ロード/ストアパイプラインを増やすとか、 インターリーブを増やすとかで性能を上げる、という方向は XMP の頃は間違っ ていなかったのです。

Cray-1 のプロセッサはおよそ 25 万ゲート、つまり 100万トランジスタ程度 であったようです。これに対して、現在の 90nm テクノロジーでは数億個のト ランジスタを集積することができます。従って、単純計算では Cray-1 のプロ セッサを数百個集積できます。実際、初めてほぼパイプライン化された 演算器を集積した Inte i860 は 1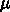m テクノロジーであり、現在のテクノ ロジーの 1/100 以下のトランジスタしか集積していませんでした。

しかし、 SX-8 は、パイプラインを 4 セット持つとはいえ1プロセッサしか集 積していません。 つまり、大雑把にいってトランジスタ数から可能と思われ る数の 1/100 の演算器しかもっていない、ということになります。何故でしょ うか？

これは、必要なバンド幅でメモリとつなぐことができないからです。 SX-8 プ ロセッサチップのダイ写真を見ると、チップ面積の大半が I/O のためのパッ ドになっています。巨大なチップ (20mm角)であるにもかかわらず、論理回路 の占める面積はほんのわずかです。それでも、メモリ転送速度は 64GB/s と2 演算に対して 1 語転送です。

このことは何を意味するでしょうか？ Cray-1 において大した追加コストなし にベクトル命令を実装でき、さらに XMP において大した追加コストなしで 間接アクセスを可能にできたように、現在では殆ど追加コストなしに 演算器を増やすことができるということです。

増やした演算器を有効に使うことができるか？という問題はもちろんあるでしょ う。しかし、現在のベクトルプロセッサではもっとも貴重な資源は演算器では なくチップ/ボード間配線となっているのです。従って、貴重な配線資源当り の性能を最大化するのがアーキテクトの目標でなければなりません。

天才クレイをもってしても、7600 から Cray-1 に到達するには 10 年かかっ ています。過去を振り返ってみると、 7600 の時点で既にベクトルプロセッサ は有効な解であったにもかかわらずです。ベクトルプロセッサにおいて設計の 根本的な変革が必要になったのは、 1 チップ実現が可能になった SX-6 の時 点、というのがもっとも甘い評価です。もっとも厳しく評価するなら1チップ のトランジスタ数が 100 万を超えた 1990 年前後です。いずれにしても、 10 年程度しかたっておらず、次世代のアーキテクチャがまだ見えていないの は歴史的にはやむをえないのかもしれません。

しかし、SX-8 の問題は、スカラマイクロプロセッサに対して価格性能比が大 きく悪くなってしまった、という点にあります。結局、スカラマイクロプロセッ サではチップ間転送速度が演算器に対して不足するにまかせて演算性能を上 げる、という選択をしたからです。これにより実行効率が悪いという問題があ るにせよ、チップ間転送速度当りの実効演算性能はスカラマイクロプロセッサ はベクトル計算機に比べてはるかに高くなっており、結果的に総合的な価格性 能比も良くなっているわけです。

ベクトルアーキテクチャには革新が必要です。

2005/12/7 記

Previous

ToC

Next