| Previous | ToC | Next |
前回 2 について、佐野氏から twitter でご意見をい
ただきました。 twitter は 140字で式も図も書けないので、科学的・数学的
にきちんとした議論にむいているとはいいがたいと思います。ということで、
ここでまとめて回答させて下さい。
佐野先生の、私に対するツィートのうち私が答えるべきものは以下
のうち、3-5 だと思います。以下順番に。
3は
3. 交通整理の続き (2020/4/16)
他の2名から科学的な議論は遠慮せず行うべき、とのことですので、誤解に
ついて説明します。長いので、3回に分けて。1)人口保存は、反応速度論
的には守らないと物理的な意味が脆弱。感染者が少ない時は誤差は少ない
が、爆発が起こる場合は変動が1のオーダーになるので致命的。2)は長
いので最後に。
です。これについては、私も 2.1 で同じことを、されている近似はど
のようなものでどう問題が起こるかまで含めて書いています。
爆発が起こる場合は変動が1のオーダーになるので致命的というのは、ここに現れる誤差は潜伏期にある人の全人口に対する割合だけな ので、通常はそこまで大きくなることはないはずです。佐藤氏の
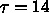 日だとかなり大きくなりえるのですが、これはパラメータが適切
ではないと思います。
日だとかなり大きくなりえるのですが、これはパラメータが適切
ではないと思います。
4 は
4)東京都の予測で、(増幅率:α=0.57010、回復率β= 0.0137)としてい ますが、単純なSIRモデルなら、R0=43となり大きすぎます。遅延がある場 合、R0は単純にα/βではありませんが、多くの都市で、退院までの日数約 100日は平均としては長く取りすぎです。そもそも入院したら感染はさせま せん。です。これは、 1.3 で既に書いた通りであり、このこと自体に意見 の相違はありません。 2.4 に書いた通り、これと「最悪条件」は別の話です。
5 は
2)t=0で感染した人がτ日後に感染させる感染させる確率をf(τ)とすると、 拡張したSIRモデルは次の式になります。ここで簡単のために f(τ)=δ(τ—h)のδ関数とすると、積の項はS(t)I(t-h)になります。(hは 佐藤氏の遅延τに相当します。)それでも近似ですが、佐藤氏のように S(t-h)I(t-h)にはなりません。これも 2.2 で議論した通りで、上の近似では佐藤氏の 式にはならないのですが、私がいっているのはそれは 出版された論文 の図1の状態遷移図にあるように「inapparent infection」がモデル方程式に 実効的にはいっている(のに変数として陽的に書かれていない)からである、と いうことです。一次遅れ(線型遅延)ではない、固定時間の非線型遅延をいれた SEIRモデルであるともいえます。
それを考慮すれば(さらに上の総人口が保存しないという問題も解消する形に 方程式系を修正すれば)、佐藤氏の方程式系はコンシステントなものであり、S(t)I(t-h) でないから間違い である、というのはいかがなものか、というのが(繰り返しですが)私の主張で す。(総人口が適切にはいっていない、というのはその通りで、それは上で議論したものです)
| Previous | ToC | Next |